Comando TrigCombina

TrigCombina

Categorías de Comandos (todos)

• 3D
• Álgebra
• CAS
• Cónica
• Diagrama
• Discreta
• Estadísticas
• Financieros
• Funciones y Cálculo
  • Coeficientes
  • Curva
  • Denominador
  • Derivada
  • Extremo
  • Factores
  • Grado
  • RaízCompleja
  • ... y otros
• GeoGebra
• Geometría
• Guion (scripting)
• Hoja de Cálculo
• Lista
• Lógica
• Optimización
• Probabilidad
• Texto
• Transformación
• Vector y Matriz

TrigCombina[ <Expresión> ]

Transforma una expresión que incluye productos de funciones trigonométricas en una que los transforma en una combinación de sumas equivalentes.

Ejemplo:
TrigCombina[sin(x) cos(3x)] da, tanto en en la vista CAS como en la Algebraica.

\frac{sen(4x)-sen(2x)}{2}

TrigCombina[ <Expresión>, <Función Destino> ]

Transforma una expresión que incluye productos de funciones trigonométricas en una que los transforma en una combinación de sumas equivalentes, priorizando y tendiendo con preferencia a la función dada.

Ejemplos:

TrigCombina[ (tan(x) +tan(y))/(1-tan(x) tan(y)), tan(x)] da tan(x + y)

TrigCombina[ (tan(x) +tan(y))/(1- tan(x) tan(y)), tan(y)] da tg(x + y)

---

Atención: Los resultados de sendas funciones multivariables se registran tanto cuando se ingresa la expresión desde la Barra de Entrada como si se anotara en la Vista CAS sin el de correlato gráfico ni en uno ni en otro caso.

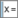En Vista CAS C_omputaciónA_lgebraicaS_imbólica

El comando obra del modo ya descripto, admitiendo literales en operaciones simbólicas.

Ejemplos:

TrigCombina[ sin(p) cos(3 x)] da

\frac{sen(p - 3 x) + sen(p + 3 x)}{2}

TrigCombina[ (tan(k p)+tan(x))/(1-tan(k p) tan(x)),tan(x)] da:
tan(k p + x)

TrigCombina[ñ sin(x) + ú cos(x)] da...

\sqrt{ñ² + ú²} cos(\frac{1}{2} π sgn(ñ) sgn(ú) - \frac{1}{2} π sgn(ñ) - arctan(\frac{ñ}{ú} ) + x)

TrigCombina[ñ cos(á x + δ) + ú sen(á x + δ)] da...

\sqrt{ñ² + ú²} cos(á x + δ + \frac{1}{2} π sgn(ñ) sgn(ú) - \frac{1}{2} π sgn(ú) - atan(\frac{ú}{ñ} ))

Nota:

• Ver también los comandos TrigDesarrolla y TrigSimplifica.

Combinación Lineal Generalizada en Vista CAS

Una combinación lineal general se evidencia en el último ejemplo:

TrigCombina[ñ cos(á x + δ) + ú sen(á x + δ)] da...

\sqrt{ñ² + ú²} cos(á x + δ + \frac{1}{2} π sgn(ñ) sgn(ú) - \frac{1}{2} π sgn(ú) - atan(\frac{ú}{ñ} ))

Si la pregunta fuese, en particular, si f(x) = cos(x - π/4 ) es o no, dentro de los reales, una combinación lineal de:
f₁(x) = cos(x) y
f₂(x) = sen(x)
... podría partirse de:

• reformular f(x) como f(x) = sen(x + π/4 )
• rescatar la misma identidad trigonométrica:
  

  ---

  sen(a + b) = sen(a) cos(b) + cos(a) sen(b)

  ---

• corroborar que para x ∈ R...
  sen(x + π / 4) = cos(π/4) sen(x) + sen(π/4) cos(x)
  De lo anterior, se desprende que:
  f(x) = \frac{\sqrt{2} }{2} f₁(x) + \frac{\sqrt{2} }{2} f₂(x)
  ... se cumple ∀x ∈ R.
  Es decir:
  f(x) = \frac{\sqrt{2} }{2} f₁(x) + \frac{\sqrt{2} }{2} f₂(x)