Comando Extremo

De GeoGebra Manual
Extremo
Categorías de Comandos (todos)
- Extremo( <Polinomio> )
- Calcula numéricamente, crea y grafica todos los puntos correspondientes a extremos locales de la polinómica dada.
- Ejemplos:
Extremo[x³ + 3x² - 2x + 1]crea los puntos de coordenadas aproximadas(0.29, 0.696)y(-2.3, 9.3)y los graficaExtremo[(x⁴ - 3x³ - 4x² + 4) / 2]crea los puntos correspondientes a los extremos de coordenadas aproximadas:
(-0.68, 1.65), (0, 2), (2.93, -16.05)
- {Extremo[ <Polinomio> ]}
- Lista todos los extremos locales del polinomio en tanto lista de puntos)}}
- Nota: Si se encierra entre llaves el comando, el resultado lista los puntos correspondientes.
- Ejemplo:
{Extremo[(x⁴ - 3x³ - 4x² + 4) / 2]}crea la lista de los puntos correspondientes a los extremos de coordenadas aproximadas:
(-0.68, 1.65), (0, 2), (2.93, -16.05)
- Extremo( <Función>, <Valor xInicializquierdo>, <Valor xFinalderecho>> )
- Calcula numéricamente, crea y grafica el punto correspondiente al extremo de la función en el intervalo abierto
(<xizquierdo>, <xderecho>) - Nota: La función debe ser continua en el intervalo indicado por
[ <xizquierdo>, <xderecho> ]. De no serlo podrían obtenerse "falsos" extremos próximos a las discontinuidades. - Ejemplos:
Extremo[(x⁴ - 3x³ - 4x² + 4) / 2, 0, 5]crea solo el punto (2.91, -16.05) el único de sus tres extremos - (-0.68, 1.653), (0, 2), (2.93, -16.05) - dentro del intervalo entre 0 y 5Extremo[(x⁴ - 3x³ - 4x² + 4) / 2, x(X_i), x(X_f)]crea, según la ubicación que sobre el eje x de los puntosX_iyX_f, un punto coincidente con uno de los extremos o uno que queda indefinido.
El punto extremo queda indefinido si la posición de los puntosX_iyX_fque establecen el intervalo, fuera inadecuada.Extremo[cos(3 pi x) / x, 0.1, 1.1]da por resultado tres puntos que representa gráficamente extremos de \frac{cos(3x π)}{x} en el intervalo especificado y cuyas coordenadas aproximadas se listan a continuación...
(0.297, -3.17)(un mínimo)(0.65, 1.52)(un máximo) y(0.99, -1.006)(otro mínimo)
Los lista como {(0.297, -3.17), (0.65, 1.52), (0.99, -1.006)} si se ingresa entre llaves { } como{Extremo[cos(3 pi x) / x, 0.1, 1.1]}
 Atención: Para mejor interpretar la información provista, es conveniente contar también con el gráfico de la función.
Atención: Para mejor interpretar la información provista, es conveniente contar también con el gráfico de la función.
 En la Vista ComputaciónAlgebraicaSimbólica
En la Vista ComputaciónAlgebraicaSimbólica
Sin admitir literales, el comando obra como ya se ha descripto.
Para algunas variantes es viable operar con el comando encerrñandolo entre llaves { } para que el resultado sea una lista.
 Atención: En esta vista se ofrece solo el primer extremo numéricamente encontrado en lugar de establecerlos o listarlos exhaustivamente.
Atención: En esta vista se ofrece solo el primer extremo numéricamente encontrado en lugar de establecerlos o listarlos exhaustivamente.
- Ejemplos:
Extremo[(x⁴ - 3x³ - 4x² + 4) / 2]da por resultado, con decimales según redondeo, (-0.68, 1.65) el primero del conjunto {(-0.68, 1.65), (0, 2), (2.93, -16.05)} de extremos
Empleando las llaves para obtener la lista del conjunto de extremos:
{Extremo[(x⁴ - 3x³ - 4x² + 4) / 2]}da por resultado, con decimales según redondeo, la lista de extremos {(-0.68, 1.65), (0, 2), (2.93, -16.05)}
Nota:
Ver también las herramientas: la de  Inspección de funciones en este caso y los comandos PuntoInflexión, Mínimo y Máximo
Inspección de funciones en este caso y los comandos PuntoInflexión, Mínimo y Máximo
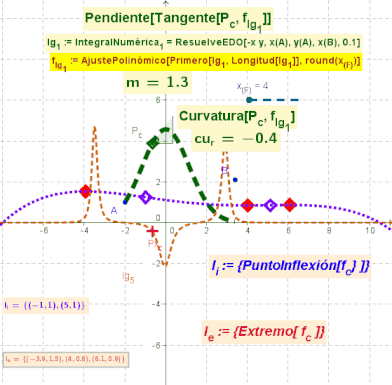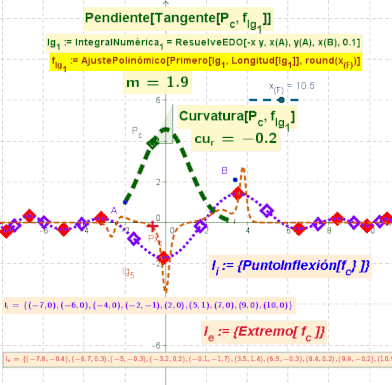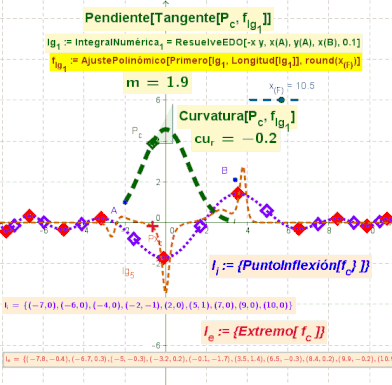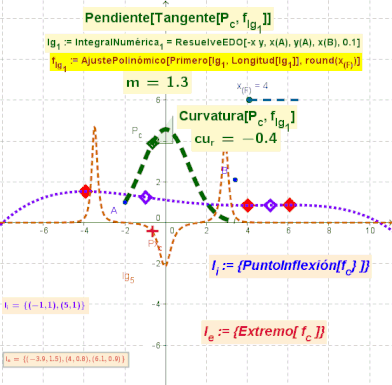
El boceto ilustra animadamente la posición de los puntos de Inflexión en azul y de los extremos en rojo, sobre la curva de una función que surge del AjustePolinómico de un lugar geométrico.