|
|
| Línea 6: |
Línea 6: |
| | }} | | }} |
| | ==¡Tantas formas de Trazar un Cuadrado!== | | ==¡Tantas formas de Trazar un Cuadrado!== |
| − | Para algunas de las posibles construcciones del cuadrado se suelen emplear [[Herramientas|herramientas]] como las listadas. Conviene, antes de ponerlas en juego en alguna de las variantes de trazado que se intente, llegar a dominar su empleo:
| + | Acaso un inicio [[Tutorial:Hacia_el_Algebra_desde_la_Barra#Desde el Cuadrado|"cuadrado"]] permita considerar modalidades y variantes de trazado hacia el dominio de comandos y herramientas. su empleo: |
| | | | |
| − | {|border="1" cellpadding="10"
| + | {{Note|1=<br>Son ilustrativos también los tutoriales [[Tutorial:Diagonales Cuadradas|Diagonales Cuadradas]]. [[Tutorial:Hacia_el_Algebra_desde_la_Barra#Desde el Cuadrado|Desde el Cuadrado]] y [[Tutorial:Cuadrilátero EquiDiagonal]]}} |
| − | |[[Image:Mode move.png]]||[[Herramienta de Elige y Mueve|Elige y Mueve]]
| |
| − | |-
| |
| − | |[[Image:Tool Regular Polygon.gif]]||[[Herramienta de Polígono regular|Polígono regular]]
| |
| − | |-
| |
| − | |[[Image:Mode showhideobject.png]]||[[Herramienta de Objeto (in)visible| Objeto (in)visible]]
| |
| − | |-
| |
| − | |[[Archivo:Tool Move Graphics View.gif]]||[[Herramienta de Desplaza Vista Gráfica|Desplaza Vista Gráfica]]
| |
| − | |}
| |
| − | | |
| − | ===Preparativos===
| |
| − | *Abrir una '''Nueva Ventana''' desde el [[Menú Archivo]]
| |
| − | *Establecer, en el [[GeoGebra_Manual:AlRespecto#Interfaz GG|Menú Apariencias]], la de '''''Geometría'''''.
| |
| − | *Establecer que el '''Rotulado''' se aplique a '''Solo puntos nuevos''' en el [[Menú de Opciones]]).
| |
| − | ====Cuadrados Variados con sus Alternativas y Variantes====
| |
| − | Es posible construir un cuadrado de muchas y diversas maneras, empezando por...
| |
| − | *la más directa (empleando la [[Herramienta de Polígono regular|herramienta de Polígono regular]], indicando un '''''4''''' en la caja de diálogo que se despliega tras marcar el par de puntos que determinarán el par de vértices de uno de los lados. {{Note|1= Para un hexágono, habría que ingresar '''''6''''' y así según el polígono que se desee}}
| |
| − | *una interesante es la que apela a uno de los Teoremas de Thales y que se desarrolla en la sección correspondiente,
| |
| − | *las que aparecen en otros tutoriales que se pueden recorrer, como el '''''Cuadradeando'''''
| |
| − | *las que se pueden lograr con las [[Transformaciones|herramienta de transformación]] (ver ejemplo en esta misma sección).
| |
| − | ... a continuación se describe una variante ('''''La de Mileto''''') asociada al [[:w:es:Teorema_de_Tales#Segundo_teorema|segundo teorema de Thales]] y en '''''Cuadrileteando''''', una modalidad con variantes sofisticadas al punto que se incluye un campo de entrada para establecer la longitud del lado.
| |
| − | ===La de Mileto... Recuerdos ''¿escolares?''...===
| |
| − | Antes de empezar, conviene recordar una propiedad asociada al [[:w:es:Teorema_de_Tales#Segundo_teorema|segundo teorema de Thales]] que puede rememorarse ''en acto'' revisando la aplicación [http://www.geogebra.org/en/upload/files/Practice_jr/02_Theorem_Thales.html Theorem_Thales.html] y/o llevando adelante la siguiente construcción, para la que vale ir alistando estas [[Herramientas|herramientas]]:
| |
| − | | |
| − | {|border="1" cellpadding="10"
| |
| − | |[[Image:Tool Perpendicular Bisector.gif]]||[[Herramienta de Mediatriz|Mediatriz]]
| |
| − | |-
| |
| − | |[[Image:Tool_Semicircle_through_Two_Points.gif]]||[[Herramienta de Semicircunferencia|Semicircunferencia]]
| |
| − | |-
| |
| − | |[[Image:Mode point.png]]||[[Herramienta de Punto|Punto]]
| |
| − | |-
| |
| − | |[[Image:Tool_Polygon.gif]]||[[Herramienta de Polígono|Polígono]]
| |
| − | |-
| |
| − | |[[Image:Tool_Angle.gif]]||[[Herramienta de Ángulo|Ángulo]]
| |
| − | |-
| |
| − | |[[Image:Mode move.png]]||[[Herramienta de Elige y Mueve|Elige y Mueve]]
| |
| − | |-
| |
| − | |[[Image:Tool Intersect Two Objects.gif]]||[[Herramienta de Intersección|Intersección]]
| |
| − | |-
| |
| − | |[[Image:Tool Midpoint or Center.gif]]||[[Herramienta de Medio o Centro|Medio o Centro]]
| |
| − | |-
| |
| − | |[[Image:Tool Reflect Object in Point.gif]]||[[Herramienta de Simetría Central|Simetría Central]]
| |
| − | |}
| |
| − | | |
| − | ====Rectos Dinámicos====
| |
| − | <center><ggb_applet width="460" height="273" version="4.4" ggbBase64="UEsDBBQACAAIACSq4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACSq4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vvdbts4Fr7uPAWhi71KHPFHlNR1OkjSDqZAOi0m3cVibxa0xNicyJJXkh07mJfa6bzB3veZ9pCUZMl23Dg/3bqIEUM/POIhz/edj0d02/9xPk7QTOaFytJjB/dcB8k0ymKVDo+daXl5GDg/vvqhP5TZUA5ygS6zfCzKY4dpSxUfO6Hnu64ro0MyINEhw/7locBBcOiHgyDySSgDLByE5oV6mWa/iLEsJiKSF9FIjsV5FonSOB6V5eTl0dH19XWvdtXL8uHRcDjozYvYQTDMtDh2qpOX0F3noWtqzInr4qN/vDu33R+qtChFGkkH6SlM1asfXvSvVRpn1+haxeXo2AncwEEjqYYjmJPnMwcdaaMJBGQio1LNZAGPti7NnMvxxDFmItXtL+wZSprpOChWMxXL/NhxewQz7AZh83VQliuZlpUtrnwe1b31Z0pe2271mfGIuYNmqlCDRB47lyIpYE4qvcwhns11US4SORDgs8yncL0cDj4g0KxuwBa7gJuNwbFzyA7gD2Jw0Ey97bPl0va4g8faHydk6Q+cH+gvhy/TA1nxCGMosywxPbro998RcYmLDvQB2wOBA+e2ybX3XGoPxB6YPXjWhtnHmTVl1oZZG0Z3iWl1Y8MUMQ7vPkXygKDSxqNP1z0Sb7NHSrZM07q4A47YuzNvONvB4Zawtj3C3Myf+dYJU+dJvyINKkbatgprKceFphENkRdqNmDkAWU8hEPEfeQTBARB2EMMbgXACB9RH+4xRFGAQriBKTJU8XQr800fHHkYcYZ8F3HgGMLggCGPImwoxhAQCxmaAmUJBQvPQx485esOie6DcsQ4XNEAMRibZqiPwZDCg3AN/gmiGFH9MPYR4Yjr/jDTzOeBHjZ0SRCHIWDdIZAcCG7JDfYBop5OkypMKp1My05oonFcn5bZpMEArEGEllK3QfjOVaJEKnYQv4B699K7x0gTzoO90J4vTfAJpGd3uVuKT7ghqreJz9Z16/G04GnlbrvDZ7n7puROBwWJuSyaYA9zDdNS5B5fEncqBjG5nyLubQWI90OF96sC5Bs8fsUK8FkSnyWxlsQXnWsDRyIGMlHp8EKjjNBMJJr3xtFllpaoBpjZe8NcTEYqKi5kWcJTBfpNzMS5KOX8J7Buhm1soywtPuRZeZYl03FaIBRliduMOUtw65y0zmnrnDWzgQuvfcHbF/5Gxxm0oGkhYQBZXtS9ijh+qy2WSQyhfJ8mi9NciqtJpsw8jK2JoNmN6MtplKgYSuq/A5ENVBAXVG9OmHfnenOCBrQeR5bHF4sC2I3m/5R5BqF1SS9sf3wHLaqmINA7NUUkdC6ysGsXAEUWVZvngqHxIGcNEBtYY+erz98Wp1my5JGZ5JmYlNPc7B5BHud67CfpMJGGCeZeNJLR1SCbX1gKUNvXx8UErqoBDIYmuAjUgXiwWg6r48AejY0eWWPlGhvXWLg1p1TctOOQGAtzHNijsQKS2qFVM8X1LLFbu1GF0TTXqbKj1itNcb24T1NVntcXpYquqqlWD/wyHQ/kkifa4LWy21J2v63rBu/qBq+4qZ7b6Kd/tEK4/pXMU5lU9AbIp9m0sOnaYn4sIzWGy04eC43q32BQ9m4sh7ms7EViNvBsXE2r26bu2m3T1U95Nn6bzj4CZVYG0D+qR9kvolxNNDMhLulwKoYwN1kApLB6XMklFWNVCFh84nYvOjsBg0gvMhCeUgfvV9CsDFgO3aF3KpFlBpk8LUdZ3rzroguh4v9+SlEs0ZlM8wydisEAPIMXUChAQ+dxIsdQz6HSsNgkQgPdidNocDb4DRw2a6xtbwUa2jdS2pBfJJOR0CVkFbVELGTeiaPp8F0Wr0YXwDOTBsmYWMJMpLRcswOGkwl0Z7K2o3gAV4HmUCbSng9V3AKG0gNtuWkx10xW57J1Stt3V5AG+tk4fSFip99DxMCrjRjt6frrEUIWZeOxSGOUmjLqQo5VpPIokc5y/Rau5hsSWAfRBmha1g2R7bDqZg0DyA8VTUS+xCFax6GrSluBMO8ZRo/vDcRSnUsoD67g5aiwrwhmwNS1Zz+rOJambrSrlxrKdKYTO4fqYO5Wv2osXDsAdFPfmWMLE7Th6tYNbsEEHMjVHJ3U9ie11QnUFWGPcF3mntCq2xOmW0NYzk48kzBuPZ5/p3YOhRVsNZ4kgFzZ4JNoGr1NS5BvadRpXYGvpJzoFfJ9+jEXaaF/hLE2y4LiNp6cQwxPVWHicVemiO1M0bA0HBAPSdZH4IiYzrVQ54tuQFbUi4dr9ZEBn+PV+5Coh16P+Cxwmw9+CB23wH87ag0dViCLLGRiDbLXtmE7cF2ZfX0/5DTrh/YwsIenhI70CO2WrAY61gu8zu0nUNh3KrYBu2PWvNkl+G/2IfhWz8waBjnwFBHO8zVVqpj8Zp3ifxGTrPjrThSvHtmLWHNiYo17mLvtz1NE/tbqoYp+K9YdDOJda4j4W10enmuLh9cWHzbIY7zGmbNdMvbs/82Xx6n9OSaYURZQirGHQ15lNvc9TIMgoG7IccC2Jra3ObHJPST17DZJPdtdUs8eIqlfueojzA887mHOg4DVhQNlLOAYYx66NMDeE2DwIUsWwyxdAeHUgqCxILaKoB0Auu9qUxHnyj4xsE9E/8L2GWFOQBKiu6FnB9O81Nmeb5VAUtN8swLeG/Jq400fG9DxLqDfvntQyKG+akYyeBg5N4308ekJYtAlYli/k3h0VTsMQ4MQZMMjHg0Z97yt7yRfwPCrrxrb4dLE3gPAoEJzSRuxql4DncG8qzM3Wme4HxLqez4FQ+av7TfvLVxib+BaSTAL11p+Ve/8fo97jAJUhAcAG+HfDWDRY6zYX0sUuymmd3HN6+eGDDvEbo9Rj4TMZ9z1YFn39wiybsVgfiJb3eqxC/VqZfD5P7Yq+PyHLQs+f7JVwec/t9cB5keWBm3oRfcLw5tWILGejwnUpmEAgWc8fOByv17h3XWxf8DCJvKo9WJc0y5Jsutf5WUi5ybMa7jdwsvbE2wllH98Y6F8f3lZyFKnU7XNicn3EehP31ig9ziUf34hlMFzLNuxPGr/eGz++Ub1n1Re/Q9QSwcIjzGW3AsJAABBMwAAUEsBAhQAFAAIAAgAJKrhQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAkquFAjzGW3AsJAABBMwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKIJAAAAAA==" language=es /> </center>
| |
| − | | |
| − | ====Rectos a la Mileto====
| |
| − | <table border="1">
| |
| − | <small>Liliana Saidón de Cenro Babbage</small>
| |
| − | <tr>
| |
| − | <th>Nº</th>
| |
| − | <th>Nombre</th>
| |
| − | <th>Herramientas</th>
| |
| − | <th>Definición</th>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#0000FF">1</span>
| |
| − | <td><span style="color:#0000FF">Punto A</span>
| |
| − | <td><span style="color:#0000FF">[[Image:Mode point.png]]</span></td>
| |
| − | <td> </td>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#0000FF">2</span>
| |
| − | <td><span style="color:#0000FF">Punto B</span>
| |
| − | <td><span style="color:#0000FF">[[Image:Mode point.png]]</span>
| |
| − | <td> </td>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">3</span>
| |
| − | <td><span style="color:#006400">Arco c</span>
| |
| − | <td><span style="color:#006400">[[Image:Tool_Semicircle_through_Two_Points.gif]]</span>
| |
| − | <td><span style="color:#006400">Semicircunferencia a través de A y B
| |
| − | Esta es la primera semicircunferencia, a oculta a posteriori.</span>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">4</span>
| |
| − | <td><span style="color:#006400">Recta a</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Perpendicular Bisector.gif]]</span>
| |
| − | <td><span style="color:#006400">Mediatriz A, B
| |
| − | Esta mediatriz permitirá establecer los puntos en que, además de rectángulo, el triángulo formado por el diámetro y el par de segmentos que confluyen sobre un punto de la semicircunferencia, es isósceles.
| |
| − | </span>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#404040">5</span>
| |
| − | <td><span style="color:#404040">Punto D</span>
| |
| − | <td><span style="color:#404040">[[Archivo:Tool Intersect Two Objects.gif]]</span>
| |
| − | <td><span style="color:#404040">Punto de intersección de c, a</span>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#404040">6</span>
| |
| − | <td><span style="color:#404040">Punto E</span>
| |
| − | <td><span style="color:#404040">[[Archivo:Tool Midpoint or Center.gif]]</span>
| |
| − | <td><span style="color:#404040">Punto Medio de A, B</span></td>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#404040">7</span>
| |
| − | <td><span style="color:#404040">Punto D'</span>
| |
| − | <td><span style="color:#404040">[[Archivo:Tool Midpoint or Center.gif]]</span>
| |
| − | <td><span style="color:#404040">D reflejado en E
| |
| − | Este punto permite establecer, junto con el anterior, el par necesario para trazar otra semicircunferencia, adecuada para contar con un vértice más, el del rectángulo o cuadrado en marcha.</span></td>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">8</span>
| |
| − | <td><span style="color:#006400">Arco d</span>
| |
| − | <td><span style="color:#006400">[[Image:Tool_Semicircle_through_Two_Points.gif]]</span>
| |
| − | <td><span style="color:#006400">Semicircunferencia a través de D y D'
| |
| − | Semicircunferencia adicional, sobre la que se trazará el vértice del rectángulo o cuadrado en marcha, a representar.</span></td>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">9</span>
| |
| − | <td><span style="color:#006400">Punto C</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]</span>
| |
| − | <td><span style="color:#006400">Punto sobre d</span>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">10</span>
| |
| − | <td><span style="color:#006400">Punto C'</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Reflect Object in Point.gif]]</span>
| |
| − | <td><span style="color:#006400">C reflejado en E
| |
| − | Este punto adicional, reflejo de C en el punto medio '''E''', operará como el cuarto del rectángulo o cuadrado en marcha.</span>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006666">11</span>
| |
| − | <td><span style="color:#006666">Cuadrilátero cuadri</span>
| |
| − | <td><span style="color:#006666">[[Archivo:Tool Polygon.gif]]</span>
| |
| − | <td><span style="color:#006666">Polígono B, C, A, C'
| |
| − | Este dibujo representará a un rectángulo y a un cuadrado cuando quede ubicado uno de los vértices sobre el punto en que la semicircunferencia se interseca con una mediatriz, la del diámetro (o de una de las diagonales del cuadrilátero trazado).</span></td>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">12</span>
| |
| − | <td><span style="color:#006400">Ángulo α</span></td>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Angle.gif]]</span>
| |
| − | <td><span style="color:#006400">Ángulo de cuadri</span></td>
| |
| − | </tr>
| |
| − | </table>
| |
| − | | |
| − | {{Note|1=<br>Ver también, para seguir procurando construcciones, los Tutoriales [[Tutorial:Diagonales Cuadradas|Diagonales Cuadradas]] y [[Tutorial:Cuadrilátero EquiDiagonal]]}}
| |
| | | | |
| | ===Estrellas Fraccionadas a Polígonos y...¿Cuadrados?=== | | ===Estrellas Fraccionadas a Polígonos y...¿Cuadrados?=== |
| − | Se ofrece un escenario creado para establecer construcciones, a partir de una circunferencia en que se gira una '''''fracción de vuelta''''' un segmento de radio para unir los vértices.
| + | En el desarrollo de [[Tutorial:Hacia_el_Algebra_desde_la_Barra#De Estrella a Cuadrado|un escenario "estelar"]] se construyen alternativas de exploración, a partir de una circunferencia en que se gira una '''''fracción de vuelta''''' un segmento de radio para unir los vértices. |
| − | {{Note|1=Según el valor que se le asigne a los deslizadores -'''''numerador''' y '''''denominador''''' - se conforma un dibujo que puede resultar, eventualmente, represent]]ativo de un Polígono regular.}} | + | {{Note|1= Son ilustrativos también los diversos tutoriales [[Tutorial:Hacia_el_Algebra_desde_la_Barra|en "barra"]] a rediseñar y explorar.}} |
| − | El desafío, tras una serie de exploraciones más o menos libres que lleven a encontrar las relaciones causales entre los valores de los deslizadores y el resultado gráfico, sería: | + | El [[Tutorial:Hacia_el_Algebra_desde_la_Barra#De Estrella a Cuadrado|desafío]] plantea, tras una serie de exploraciones más o menos libres que lleven a encontrar las relaciones causales entre los valores de los deslizadores y el resultado gráfico, sería: |
| | *establecer los distintos valores de la fracción expuesta que permita obtener el dibujo representativo del cuadrado. Sea... | | *establecer los distintos valores de la fracción expuesta que permita obtener el dibujo representativo del cuadrado. Sea... |
| | **directamente dado que lo que se evidencia es el dibujo de una figura de cuatro lados, por lo pronto | | **directamente dado que lo que se evidencia es el dibujo de una figura de cuatro lados, por lo pronto |
| − | **indirectamente dado que lo que se evidencia es un dibujo tal que uniendo algunos de los puntos que quedan expuestos con la [[Herramienta de Polígono]] lleva a la representación de un cuadrado. | + | **indirectamente dado que lo que se evidencia es un dibujo tal que uniendo algunos de los puntos que quedan expuestos con la [[Herramienta de Polígono]] lleva a la representación de un cuadrado |
| − | | + | Finalmente, es posible ampliar [[Tutorial:Hacia_el_Algebra_desde_la_Barra#Circulando de inscriptps a circunscriptos|la experimentación al circunscribir e inscribir figuras de análisis]]. |
| − | {{Note|1=<br>Ver también los Tutoriales [[Tutorial:Preparaciones Espiraladas|Preparaciones Espiraladas]] y [[Tutorial:Resolver Problemas Ilustrándolos|Resolver Problemas Ilustrándolos]] <small>(de '''Diseño de ''Centro Babbage''''')</small>) }}
| |
| − | | |
| − | ====Polígonos y Estrellas Fraccionadas====
| |
| − | En la figura pueden verse:
| |
| − | *el contenido de la [[Vista Gráfica]] del escenario en cuestión para una instancia acorde a los valores asignados a los deslizadores - '''''Numerador''''' y '''''Denominador''''' - que determinan la '''''Fracción''''' de giro de la vuelta para establecer cada vértice sobre la circunferencia
| |
| − | '''[[File:Vértices.PNG|470px|center]]'''
| |
| − | *el resumen del [[Manual:Protocolo de Construcción|Protocolo de Construcción]] del escenario creado.<br>'''[[File:Verticeando .PNG|500px|center]]'''
| |
| − | | |
| − | ====Boceto Estrellado Dinámico====
| |
| − | <center><ggb_applet width="590" height="373" version="4.4" ggbBase64="UEsDBBQACAAIANyg4kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc42W2aqsShKG7/spFuu2oJ0thb0POM9DaTmUN42W6TyVsz79qbV3Q59e3Q2dYJBE+McfJIl+P56gm8H4x488T/4RD0MD5o+tTOfi5yd+JT8/ClDmxfzzE8Gxz4+PFYxT2Xfv2t/hz4+3hI0nQOI/Pz1h4ln2xnAMozAyKB4nxXxbwVeIUH99P+WzFbO4FdFHaFbPttlSjng94Wk8vWk5nqftwYV9h3Sbok5dN+Wbr5ULe2Nv7vZUkArQi1N/tQu/wv/hbfy7t7AACZlOP0uqeUIFGbHWVssLUhUfyOSpaZugeRszgsAnpsIsB8rNMpqr5tD6herXiUbHWY9BkX0JlGd4ZHoL54gr8nJw0PN2bZ94WOGUz4UT0BZhFJ9s+3iwFP8KizjHXiR/J6m6BHaVXzudJx5Rpz8sJOGW1ofFSROCnZuIx8Fb6MGlRTOy6p0ro44Lx4TVG8316vtclPXtwbBHuCCQQryuxSsw8JUq0RXVO6NNYm5GeoxGwQmFOHT1fDNKlii5JxGtcRoj8mbwgjn72tpXAV+ucd1UlHY7RfxiYdmkkmrQzh7BU9wDVmo5vVATTSoLwV7RfmYT0zD6+eKXExwksZBzLduWbIG5lHjosp/iaeLC5rK8OHeLXhRGyHfAPyumywV9cgw58R3WesCaqwn90D2zXalFYioCChlIWDy7sXURLF+o1D+tk1kMZladZs93HthT0FeMhkd4VLJTKZu6Jz/8RSedpTS323KIu6lLV7laXdSUhaqMWwYcgtB0qk9JcXPrU80akJISEqQesoY+X/gJrH0wr7FquMm12jUpVqmzWoqLQFMwtkvEwqNx60Sc48803HELIu6rDdOlVp2n5tGVVtFEHakOtRkQqnhShiVgqw8vb8tRheh1sRy73w2U1lJrtQWikiB8UQ+ktpvYl1mynPssjHqsbXjx2kuu06kLrKpKaaYKEXU5Q2yoAJhYYV1G3fN6OXLTNZ4ke9pKyW65YsixmG+RMFEiRc3U7roqF6ERXKm9lPds7nKTU2p59D6H4qnUj6osHJXJG2AsqhqJ1U20FM/HbqwBhl7h684Vql15EU7GuB7DB+HhHKUo6nxF3SRy6biXgk8KXPCu0hSlVkgOP8EKBHMvXWhpgLtpag/CnjV+KtpzcEgBxyDIy6zg0EbI+NZiTRvoltHYhRGqg8JYyCN2xIKNkWYkFeOxJIh5EK/5MD0R2YdVCyszfX8Z4pDA89l9NSgyPJF2FEnMq9Aw8hOPOyQv4qtRr/uzhWMG0ZeqV1g8UzWLT3k3WxGw7Kzdi0JGTI1HW+6iDXhSBux4q08oILKgakZrdPrhbhCP83JRJhCBsC+4CSraO+Lle9bLBRO9bLlkuRrBHdR5hMjWnxJDroBb9n3gBVvvwqQOzXjdWb0cOral1dhqpBckyw5ur0VVbsx5iWepNrMa6MPl5egKnSDTKI+mmMbnJOiKNMMZdgWNebRbi74s/WwRuqE6vvB6hgyHLORjghtgCZ1SXBwZ1qlLjpVPAwuKV4XWjB8M483rHfreN6XFpV0dB9vjEkku7qtkcz+HQQd3VkcfvXuk7mTY/Ei2reNib6vQxWCQQDdlhI6hUDE8bMIo3JVGtAChQ+USnemh3RsxoMdwHYU9YNGpMayCtJ56ly9ac5DMhXKjSUeEY8zTfLnEYbsCqb3ql+cG9pf1hLQ0ea4v113GAQoXobOLItf1IIYabwnmWDit2yMRob7PJrK/lYuYeI9zlWK3IJOGEGiGRsdcMtJqGIN9zvGgYeAnP6lqiAoXdl7e12/3V+eO45c5zDIU0bF5uPB+OK52MiDWvGYMfAAc9ZOwojADqQxbxhm0VkbpQE/ZIXbumSyXZC4fxjSj4KAUhe7cwQRb6T8ZGuw3csT5do3pmxdo8UZJzVRXwotORDWdR2LrhbmYBCJ8WQMbHjakezilSa/+agsSvFlpq9uCI8QupPj0gGlbE11zc1R5UukBD78v1mAo+2SMwst0aUt6ElmxUZ50TYD4iG6MXV0hqWxWqEeY2qV2r7pTNFeIdt3r1MuXyZSDNWPaqIykCQaYNCTmYngi4MiQFKdubbr6I125RHjB5SwP1oroGuhs9J3YVwzlg8t1OrG0D7VTVrUlUYXLbb7KAmfRxJaf1JmKPk3TiB4/o2JCRb4mzYuclxUY2+SuDKvktRcfLUbJX6570aEHPBSGSsbKNZ2IjjS7Js91ug0gjLMNMffa3r0P1n0/USN00Me5pF1PUVxHe9h1yujK5+29CYO5PC87BPhs+80E001iwOyJX7954TcTsExxY8QvJmByJiXFyqYf2JrU0RcLiNs7sI/vnPB7SWmToGnz6NQiRIcibcXzganDU74tcWe+/QTu3df76ssxLNYHBvTdn/+Ppmz63xjkPafI5r9e+IUv2dde2qTfmp8/Pz+yMW6B3U9TmTTg4+fHZxY3E/j8mIp+c8AEZuXZd9/yTFe28fwGNXaZ59/VeVzeRdDF7y7OF9JxTfms/6ID49iPfBk3fT4xz7lcwXeZHieg4cc4n77ZGaBb2Hj8lr33ffM/szJohu9DNzlIxljphmX+S2mZADv22wRGsR9V919DxU3z6wSecVN2+V8U0B8/oH9S7d/+BFBLBwiamyg5swcAAN8KAABQSwMEFAAIAAgA3KDiQAAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztW81y28gRPnufoguHrd2EIjGDX3pJb8na8sZVWtu1clxbUVSqITCkZgUCNABSlLWuyjVPkXOOrtxy9d15hzxJemYAEPwnLSXybqwy8TPT0z3T/XVPT5PufDsdRjDhaSaSuGuQpmkAj4MkFPGga4zz/oFvfPvoi86AJwPeSxn0k3TI8q5hS0oRdg3P7LGeTf0DJzDtA9v2/QPf6XsHpuN73HHtkIaWATDNxMM4ecaGPBuxgJ8EF3zIjpOA5UrwRZ6PHrZaV1dXzVJUM0kHrcGg15xmoQE4zTjrGsXDQ2Q3N+jKUuTUNEnrpx+ONfsDEWc5iwNugFzCWDz64kHnSsRhcgVXIswvuoZv4jIuuBhc4Joc1zWgJYlGqJARD3Ix4RkOrb2qNefDkaHIWCz7H+gniKrlGBCKiQh52jXMJmn7nmNAkgoe5wUBKQS1ShadieBXmpd8UmIITmciMtGLeNfosyjDhYi4n6ISq/csv454j6GgPB3j+2wOpEGxW7xBWiJXqRfeNQ7sBv7zTb/heLaeRl1mTaTmuIfEUp7XpjN5KLwhPy5+bDmRBYk4hzxJIsXRhF9+AWpSExryRvSN4s11dZep20xL36i+2frmaBpbD7c1qa1pbE1jW/votGhYsURC2rsvkd7GjlYl0lkhkjqrRVqbZGoROxiSODXgoCT1T32WBLr2HgI36HWLxE6rdJROgRrILiRtAdacDzOJI6sNTlvCgYCDmHGAtMH1wKOACAHigI1NPkLCA8vDNhss8KGNDcQChRVH9tqe4uGCQ8C1wTPBRZABQQE2OBYQhTEbEFmgcIqYpRZSOA44OMqTDKnkYblgu/hm+WDj3CREPYKEFg7Ed5RPwSJgycHEA+qCK/kRW0Lf9eW0kSUFF6dAJENEOSJcoxvpfbAc6SeFmkQ8GudzqgmGYfmYJ6PKBkiNUWgW4FaEu2MRCRazPUKeb31cwLtF8KncxHX9X0Xw2bbA+4g9SzJnwae9Qqvrgs/GjevuYsHncPc53BVqkkoBNuVZpexBKs00C3J3HxL3iIeUEPr/lQK65NcRhe8jBfzorY24nzPAzyHx0wiJD+belTki1uORiAcn0soAExZJ3CtB/STOoTSwrdsGKRtdiCA74XmOozL4mU3YMcv59AlSV9NWtEESZy/SJD9KovEwzgCCJDKrOScRqT3Tatb4YtU67HqHU+twa8/eSrkJ9sA44yg/SbOSnIXhU0kx82HU5PM4un6ccnY5SsT8MjotVYPo8HEQiRBT6lcIZGUq1AuUJQl1eC5LElbbKSeSpOHJdYbohumfeJrIaOA32/U/dKFr3UXbqpKTBUz6ot2ep/MRItdFn2MioZLAJ5UhVqBGL1g+P80eJ9EMR2qVR2yUj1NVM8JJpHLuh/Eg4goJqi244MFlL5meaAhYmtfL6xG+FRPoDZR2AaMDdXC3HBT3nr4rGjmzispUNKaiMEtMibDqJ1KTg+Le03dFhSDVUytWSspVErMUIzIV00yj8I4yXkmIy819HIv8uHzJRXBZLLUY8Gw87PEZUCTBd0IXo3SVbV4M2VcMWRBTjFspp9NaAFznkqcxjwp8o8nHyTjT7lqDfsgDMcTXOT9m0qp/xEnp1pAPUl7Qs0iV7bReVa9Zh+5Ss2L1JE2GT+PJS4TMwgQ6rXKWnSxIxUgiE/USD8ZsgGvjGZoUd49LPoNiKDKGm09Y5yLdE20QyE0G1ZNL5X0vUobbC7x6//cUNSZZsXF+kaTVURdOmAjf/yOGkMMRj9MEHrNeDwWjEAxQaAzpxhEfYjoHuQJxPB7yVASV7Z7JdxYmqUoTcW3jYvnELc2vInTS+xlDaLUD68HqRdFg9wLeiVmgWd5ZNLpgqshYIJtd83ROzYrj834/4zlMMfXzkcs13p1a9w9JWE6umFkkM1cYCr0xDxmO/I7HCTaoJQHrZRiJc34SoP3jWR1Xr6KIZK6MLVKo125qqa4nH/piyquQgmoXbxCFbG7ZMw/NcYu4xAQZQe4Zha6Jo5/+IMKQx9WsWYyAVYbGMDnSTjLiXPtXXoQaGKGOVKSqQa0w5Vaj1nWwYFbL/iTMSvY1q2vubU23sCah7idvzukoRWGSSWGDJykLAnw/v8FEI0/eGoA0XePL1+Mk/0Z3Ssfvwp8xcw1udDv8Hr46Zi/5T6eVW599jY269+0SVQ0ndTrkukgpJco1vsTJzJhDC+osajz0VSdk81iVyzHWrvKugWluBOYMeUWryNRyddtMmkoLM3Sx/iyFUgmCWZwV5OFHQzdnaf5C5hqg8G42XWsup/EUJJ2m69Sb8Ujypr4RrvFzlcRU2jg8T7foq7ZNrlJYmZJ8tLoWoS8DwRL4ySrw49jxVG5i6fWistU+nEnt0abjKnVZTZ/WNfSgozQhk7QiqtVbF7bwXdX5+LeuTrvpUqVO2pS15ztQZ5AMh5iiQKzOzid8INuN2YmNmRqlwIjWr9bdOC8703OmeRaclkyUFTxLE8gB92yk7YomTTLn9G2vULvpKrUfELPp+V4tAvgb9h+ntous2H7461gPKQKRGI4iEYi80nUksfI0zjEB5yqGL+fQl5yP5BnnefwSU85Mfnk+v7pdfejoPLhv82zfjdd40Mx+0jo6c2hSe6OjOKsdhW52lCORBhFf8BOpOuUnhU/M+Umw2Uvw9FDL/u7dBOs8ZCW86RZ4iwGPJ7iIJM1wSzWLH39cm3pi8KZsmRK13co+UjS9ITXLISpSMYXDkv6wpDqkONBqWm2PmrM/dNlDq5BxaCvWEhSHjnRfCYuVzifrTKIvgs32V/nBgvmDJZu/OBebrT7vepL8FnbXVieOdT/bV33Tb3uWZbq2Z7Ut4npV7Gw7bWrbnudaxPc2u6W/2i2dbfvX6zGXP8OZt8yPSY5n6VPUbwMo/A4u8fOvv+BlTRrcAHTlM+3Ll3ijatHMmj+WLVp7dH4jzunbzRaPRDYzeDniN+TsdxJdVUVvwYbSOZRBdJSly1bdwaKLJvvwbrO1VOWoMgRSLxzFEemO67Ut03c8izjeimP5fJ1t8/Fn2ZQ7n8odvd0d2O5KUy+VI3e3KEuDWlpZYiaKkqsfeT/iU2Ws9bnGTg5a5J2naKQGfJy37u2uKTu/CUWS7eOwszG/Jpe1qsi9k8+uOTrogs+mLTG6HiTxkmW1wU8/zqoNuGwAaczVKJYDbxJp42vba9Pj1VZXR11ddfXU1VfXtroSU9/0aKKHEz2eaAZEcyCaBdE8iGZCNBequdBiDpoL1Vyo5kI1F6q5UM2Fai5Uc7E0F0tzsYqlaC6W5LIll9D6rzYX1MpaSNglJOhqSOwN7fJ7lLKGMwduZx90by6q5ec3wVj+tGG+nHak2k7E6RS+HOTfIMKmDbipyu6ngNqAs7dnRVFrS02rJmRLPN8hIbuFmy+Woqwmnas5ta2iFNu0zbk/sq4YtXCKScZx/rS/4LJT+Pdf/wZT7VI3r3iKujktvPv0v+DPZ2dvl1x6cj7ajPbFerkcsLZOvotptkS3HVT1vwh1k/PBvnoZ3IFe1u4425wVU6a6m354B12oVaZT1Gr41Yd3X8/KzgDx+3/iGhL5jdikdODZGDT0jHbHGrWax212bHmmuu3Z6jYVaHPO7T2qkz27Sf2dvL5V/25S/Tqg+J8Pj/4DUEsHCKANWR20CgAAljEAAFBLAQIUABQACAAIANyg4kCamyg5swcAAN8KAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA3KDiQKANWR20CgAAljEAAAwAAAAAAAAAAAAAAAAA9wcAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADlEgAAAAA=" language=es /></center>
| |
| − | | |
| − | =====Fracciones Equivalentes y Análisis Discreto=====
| |
| − | El análisis de los resultados gráficos que se evidencian en el dibujo, relacionados a los valores que se le asignan a los deslizadores, desencadena la necesidad de establecer recursos propios de la matemática discreta que podrían abrir un temario acorde.
| |
| − | | |
| − | ===Circunscribir desde un Triángulo a un Cuadrilátero===
| |
| − | Dicen que, en tanto tres puntos no alineados determinan una circunferencia, todo triángulo puede quedar inscripto certeramente.
| |
| − | También afirman que un cuadrilátero, en tanto compuesto por dos triángulos, no siempre podrá ser circunscripto y solo será, entonces '''''cíclico''''' cuando se cumplan ciertas condiciones. En el caso del cuadrado, no hay dudas al respecto. Quedan en cuestión, entonces, los restantes cuadriláteros que podremos analizar.
| |
| − | Empezando, entonces, por un triángulo, pasemos a considerar los siguientes casos.
| |
| − | ===Empezando por el Triángulo===
| |
| − | Para trazar la circunferencia que circuncribe a un |[[Image:Tool_Polygon.gif]]||[[Herramienta de Polígono|triangulo]], puede usarse exclusivamente la [[Archivo:Tool Circumcircular Arc 3Points.gif]] [[Herramienta de Arco Tres Puntos|herramienta específica]] o el conjunto de las siguiente:
| |
| − | | |
| − | {|border="1" cellpadding="10"
| |
| − | |[[Image:Tool_Polygon.gif]]||[[Herramienta de Polígono|Polígono]]
| |
| − | |-
| |
| − | |[[Image:Tool_Perpendicular_Bisector.gif]]||[[Herramienta de Mediatriz|Mediatriz]]
| |
| − | |-
| |
| − | |[[Image:Tool_Intersect_Two_Objects.gif]]||[[Herramienta de Intersección|Intersección]]
| |
| − | |-
| |
| − | |[[Image:Tool_Circle_Center_Point.gif]]||[[Herramienta de Circunferencia (centro-punto)|Circunferencia (centro-punto)]]
| |
| − | |-
| |
| − | |[[Image:Mode move.png]]||[[Herramienta de Elige y Mueve|Elige y Mueve]]
| |
| − | |}
| |
| − | ====Preparativos====
| |
| − | Basta con...
| |
| − | *Abrir una '''Nueva Ventana''' de GeoGebra
| |
| − | *Seleccionar, en el [[GeoGebra_Manual:AlRespecto#Interfaz GG|Menú Apariencias]] la adecuada - por ejemplo, ''Geometría''.
| |
| − | *Activar, la '''Barra de Estilo''' de [[Vista Gráfica]]
| |
| − | *Determinar, en el [[Menú de Opciones]] respecto del '''Rotulado''', que afecte ''Solo a los Nuevos Puntos''.
| |
| − | | |
| − | [[Image:3_circle.PNG|center]]
| |
| − | | |
| − | ====Pasos de Construcción====
| |
| − | *Trazar...
| |
| − | **un [[Image:Tool_Polygon.gif]] [[Herramienta de Polígono|triángulo]] cualquiera
| |
| − | **la [[Image:Tool_Perpendicular_Bisector.gif]] [[Herramienta de Mediatriz|mediatriz]] de cada uno de sus lados - al menos, de un par de ellos-
| |
| − | **sl [[Image:Tool_Intersect_Two_Objects.gif]] [[Herramienta de Intersección|punto de intersección]] de un par de mediatrices.<br>{{OJo|1=No siendo posible emplear esta herramienta para establecer la intersección de las tres mediatrices, es posible encontrar la de solo un par de ellas o, directamente, indicar el punto que corresponde cuando el puntero se vincule a la lista de objetos que confluyen en tal posición.}}
| |
| − | :*una [[Image:Tool_Circle_Center_Point.gif]] [[Herramienta de Circunferencia (centro-punto)|circunferencia]] con centro en el punto de intersección que pase por cualquiera de los vértices del triángulo.
| |
| − | *Controlar ahora la construcción...
| |
| − | **Sometiendo a los elementos en juego a la ''prueba de arrastre'', de modo tal que en tofos los casos se mantenga circunscripto adecuadamente el triángulo.
| |
| − | ===Ampliando la ''Circuncripción''===
| |
| − | *Considerar...
| |
| − | **sobre qué arco de la circunferencia se podría establecer un cuarto vértice de un cuadrilátero en marcha para que su '''''diagonal''''' resulte uno de los lados del triángulo trazado
| |
| − | **hacer el intento y considerar qué tipos de cuadriláteros se pueden trazar manteniendo la condición de quedar circunscriptos por la circunferencia trazada.
| |
| − | {{OJo|1=Indagar, recíprocamente, qué tipo de cuadriláteros resultan cíclicos en una construcción como la que aparece a continuación.}}
| |
| − | ===Cuadriláteros Clasificados y ¿Cíclicos?===
| |
| − | En el escenario dinámico que se ofrece a continuación es posible explorar e indagar qué relaciones vinculan a los cuadriláteros de distinto tipo con la condición de '''''cíclicos''''':
| |
| − | | |
| − | <center><ggb_applet width="500" height="433" version="4.4" ggbBase64="UEsDBBQACAAIABM150AAAAAAAAAAAAAAAAAtAAAAMWZlNGNlMzI3NjA1MjJjMzAzMTc2YjMzYzUwZDc5MjZcQUJTVFIxOEIuUE5HAYQBe/6JUE5HDQoaCgAAAA1JSERSAAAAIAAAACAIBgAAAHN6evQAAAFLSURBVHjaxZcBEoMwCAR5Ok/zZ9bamJKTJAda2xmaGavxuhyIsizL+s+Q9xd+nrixqqIAqas9SbbY1+1nlTtX9Qj4IvaQIqZsIlaUOc6e5wgQd0UajxHwRIhNiQb/MRynCWBaakoQ+y8JeET0IokUgZ43XCNGCNi4JMLcJEQAm0NGRDVplsChrqXBpwU9cQRNoKorG2VENHtNPeEQsBdaIVGDdku11wkbAiAiY1C7Z79fdDyATrZCouk4TOo9K8YEUMTJF0ES1qBVzMQDJzFJEb1+QROwF2CZZtLyLdWZB0Zl1FTIGiJSJ6GIB/B4U2ZJgzYjGUvArZKrJCgPDNKRrRJVAQK9Zzkhxoq4nUB0DhSSxJkAiZvpF+iNPAFiyukSmoiIe4D1iCPCK9XbPMCkxZsvhgSoPhAYQu27xKdSgICW3vxU2LTIv1/PX9L/pXlCrSOXAAAAAElFTkSuQmCCUEsHCN3atIyJAQAAhAEAAFBLAwQUAAgACAATNedAAAAAAAAAAAAAAAAALQAAADE3MTcxM2YzODcxODJhMzI4MWNhOTExMjU4YWRlODk5XEFCU1RSQzEzLkpQR/t/4/8DBgEvN083BkYmBgZGIGT4f5vBmYGDjY2djZWDnZ2dk5ODi0eEl4ebm0dSSJhfRFZKXk5WSkZGQUVPXUFJR1lGRsNcU8fA0MTERF7d0tbCyEbP2MQIZAgjJycnDzePBC+vhJGijKIRyeD/AQZBDgYFBgVmRiUGJkFGZkHG/0cY5IHuZGUEAwYoYGRiZmFlY+fg5OIGKtgqwMDEyMzMxMLMysrCApStBcozsAiyCikaOrIJByayKxWKGDVOXMih7LTxoGjQxQ8qxklFTZxcYuISklKqauoamlompmbmFpZWzi6ubu4enl7BIaFh4RGRUckpqWnpGZlZxSWlZeUVlVXNLa1t7R2dXZMmT5k6bfqMmbMWLV6ydNnyFStXbdq8Zeu27Tt27jp0+MjRY8dPnDx16fKVq9eu37h56+Gjx0+ePnv+4uWrj58+f/n67fuPn79A/mJkYGaEAaz+EgT6i4mFhZmFHeQvRqZykAJBFlZFQzYhx0D2xEJhJaNGDhGniQs3HuRUNg76IJpUdJFLTMXkoepHkNfAPiPOY01k+QzuMYS/bjHwMDMCI49ZkMGeYeMj3vqQjdf1dBfuvM0lemu3yGMN/mW1VfPjao1UPk7btGRJeb9Od+PG3CtzJjGcE77Sf6ZcgeNPbPHmo9s3LPj57dh9bU0LrcW2bhxPHlseYG/8rBNVNiHvSbwW7zuHsHQfM4nPc0pOHlRIYdyR8OfM3ZCVflsX+93Ku3VRPlRqRkbiQnWOF1Nve2/bt2Z74iN5wVivxW8vP274vfYyV7mAI6Px/F38O/Isg2N9qtoWipitLSzbvXSeKpdgXcI5xidM/LIG7pK27pIPIjPKDrh1feeaEe849ff6LfP92P1mvIjapGdqWL3m5XvlRcZxB7cZVaqfDShg40/8LNjEIKm2ey5XyYqb6/rDs7c/qRAV+ag/a0plwrrbmbFbN8X53L3yxWV67M7980IjvBVTa1Y9zlp/7+W5e9UfFtsayp79Om1+mvIWrUuMT1fP0X4wweEEc/O8xeuTJ3n0HxV+df/WJvfU5LKLboJhoe6ldw5bSrv7LXg8wZypkqvSOH+N7RHfv9NXLGpRV7rk9OpOvUDov/d+hbub54Updy7nKvS9uzpjS7yZRBbfmsU6vv6ltkqzvO7q/+rfcWVapYrz3jurreZMC/5s5vB6ZxGfh4VyGV/hjDW6J66Z3FRLm9h6d1Nbuo6jkMb78/8Z1jzgc5iZox+QWLLXvd9bk/3yov7EH/y523R09P8zbC35z/BjevyitXdUu6MsApibPFUKLP7Ft5tWTVpz55Wnta7QRf2JX76qtraJ1X3JT5s66+1F+f83AVBLBwiF6DKb9gMAAJQEAABQSwMEFAAIAAgAEzXnQAAAAAAAAAAAAAAAABIAAABnZW9nZWJyYV9tYWNyby54bWztXNty20YSfU6+AoWHrb1Y0PT0XL2mU5Z8ibccW2V5U1ulTbkgEKKwIQGGgGwpLlflNV+xz/uwP7Cv/oD9h/2S7cEAlChSjC6kFTKSLQMcDoCZPt093dMHfvDV8aAfvEtHZVbknRAiFgZpnhTdLO91wqPqYMOEXz388kEvLXrp/igODorRIK46oXA9g+Myu58XL+NBWg7jJN1NDtNB/KJI4qq+3WFVDe9vbr5//z5qbxAVo95mr1dFx2U3DOjhedkJm5P7dLuJi95j3Z0zBpt/++aFv/1GlpdVnCdpGNDABnEyKoJk0HWD6IS76SDbKfphUBVFf0bT12l/2Am//fSvUZUlaRl00+BF3C2C12lSFaPgJHj56T+DlO6Yh0GWFPnTrE+3gINUJClyrZjkPEGGoNU+YiJZV1uu/v5oa/fNazBb0c7LZ2FQHhbvn+dv6HFb8agTVqMjGmtSDE+246ETDM34IO6XadiO/3k+PKqCmHXCR2EQQyfcogPvhHm42XZ5dVS1fWgyn/7de5v7rrvjj64vDbmk5yXuMUGVVW701O+oOixG7qwbV66Feqb9dJDmVVCdDKklP6JZZ0kY9OP9tO+e/PDLLx68i/tHaUD/dkJNeG+6Nje5oNj/BwmsnUZ7kZ9o+q4Tct+Xum0XfZIrPZvUhTQKGA+D/eYY94eHMX0Tge/ej0/SkX8ca1voxq8ODsq0Co5J6cLgpBNuwJkvvym6zQib1jjPBrX6BWWVDl1zUA7TtFuf+cnSUIb0rFrF/Qyc6DYbiUzJZlhkeTWe5KNwSgp+3pcXAqtFwKU8IwJ2SRFscF0LAdRMIbCbCeELUqBi1C3dk1hkyPDO/ICXPousCoMfvbOor6kFtJv92IwBz7ZWJ/2zQ7uslLduV8qmnio3y5bxBkRSjcVqFiLWpBgM4rwb5LX3I+9w0iu8OWfz3AyJ8CIXE/tu+3TATkhOIhadkLx3LDshoRArmh0ddCfs0cF0wm062E742F1Od3vijnSfp+5IN3rmh9wMdIYm+CG3WI8HU2OR5amffXWYJd/naVk6HTgVuDv5Out203zsEq6pRiDR+yx33K9vfmWPtaG9KoG+2GddbBNl2nOfxsONf8EqGnd8jfnMN4xp3T86zvpZPDrxrfUgptwHm3QfDLwoNniEXtPdGYNmpNcBNv0h95eU7t9OmA2G/SzJqrE+953tPc8rim/Sek0s/YDPGOP3aTp8Q7d+lb8ZxXnp4pvJSV0env0Vggcio5Fzo7lAAGZku7ZGQhmuLLNGayG4bHySMEg/zCJwhVLZtQEtWSHQyF5AGm3IaBBQAdaYsUgKhxcaYNIqJfzybCKprWGSWSGRS7s+kHVXCDJazUEojpaDFu6vjywikJwQk4ahZWR+6M0MIyXI6LQRUgJYZtYGs3SFMCMnSGajFFdaCakNKtGiRq6PG47McCmYa3ao8cgoFKgBJDCGTK0NagerhBp5Ry60NkZYpcGoBjVyj0AmRusWYekM0aOmKL0RFoWRnLJ6unJtQOutEmgUhwjDjQUKRlBpVHIch1grBXcuUiO5UI8ajUErRgbJKUwh14moVxa3yYx3+yYZr5NOzx/2/eHKKS+weYnKFRBFCvzPRZA+6jfyfMC55E2Ex7ci0mv6LqEtaKZBaxCk4k04LiNQFpgzDEUqv6AtgnlCe7I6QmPk8BUYDUipjFCSNztUKgJDTUxJWrqVQLt0oT1dGaGRv6WEQABlcpIxLU/1jLI7RQmDizrJwy5dZM9WRmQu65pYik49Gju/dC17W/R38bAo//wWFrLE+x3S+tOVl4u5W/F8oTuktMxTEM60Vkg+Uvj9UhlxF9MheUVDEHA+V/Zytuynt9+OhyOKHNyQ6ykFnfBFVpK4A/qmE374WF8wiVA/K08B8r2nwLl6nQTYjaOva0v/OrHUdZV9tsD5lQTOb14s+M3Ie+5Oe1tLhM+91c4mUg7OxHW22rn3DGImSEurDp7Pvm7kmefJ4bOp46nzFZGiIEqgQikkaGF9ihAJNEwp5CDcfrDxkbzbNTGKIn7NueJ6pfauJmtm9QX9uErPVc22fDns25orsPfEX733gd8LIPhTkBTl7//7U7AZ5H/46FsIk738XsC/+y74Y/A67mZH5d52Nkr66d6je8HWvWC7/uaveVY192wO7qvUzW6qO/2MhTAelg8K/JwuLqrNiCNuo8g6pahnS0ZagKLUkVZ7Y5gEaINTF8lbi5xRqF+H+Quvk+6mPxyljlQyCflYFfYuAORe0GD2uqhct+bThb236Dcj0Dn9em1xkNZ6lfkyK/gy6+PsnVeeKbzdkvdh5y18nI/41DLpr1mAe7r5WvkZV7xJmB8Nh2nePV8Nrxud1Y3F1EByxrSmINi5ovh3fuOin81EaO1u7E5rUZGNODshN0pmUxzl1fODvePgfz//Mzj2IO3M8IO7k6wFb03emDxlwTMWfslPzg6JlsE+uFyWJuGK7INzkJ9FZPMsP8x9rrllM2h0NOus9zab4NFNtHki3eOiDE7JdJ5ERycn5+hzmv7gARoNhsfIDSSxBeDSxN3UWOvpc9uA0V92lk+fc/N4+2Ej9+7zjjB3R5hb3FYFxSiglFRouFTCtMwuJZiy1hpjueYUI687fa6RuF22xCHiXKNVkmmBVhqhW4lTsuK2M1EqyV3RYTGMxTtq3a+JWid9OirnJPzrSa0j/RaUflM+JJFryaR3NEjWwMj3MA2c1B5562cA0YAkx8O0lnKlEvP1Idz5coHmlqEWCgzDZjNFCUShkZGrlbL1VBhpAs3VA4XWyu1zrw1oq0S4c8VsVAyFVKbekxBjmqQLaQWXDEEK3jLiXXUNhKHVn7BTqNYHtVXi3DkuvSujCxCKcXQxmUcNI2BojZbALTlK2dLubMSVI1ai1ISdIyqvC2yrRLsj4wFan6SuDYgJpts6KwXPXCmCSFnHY3WYcVoDKfBzrpGT/zTrY2mrxLmjkEMgQcIs+UIDRrTxN9mTJbdIpgRkT7JxjyKSWglhUUlNLhLvOHe3wyKnrIlcIygkz4i6SZB5RKeKW5BWW23Q+vBRRmRzHJQWYIykFXBlMVtPvh2Fldqlv4ZZayVojg2aCoXgHMkEmSWfunxyyurQ7cCtKIIBMmUEBeWKN5wSpZkL9Sh2cwyy5fPGVohsB5Eg2RjFSTYU8pqGbKcof9HK8auVEhyBLV/Pbodsd3ZH0S9zs3dVryBS4cJRQ4k5p2WSEj2vhSIyyEjUXGmKh/jyNwtvh4k3TdwYvwl4A4G6yMI6mr/iFBQ2715GpLaC1jvnJS0zcjF2fccZ+PUyDye2XTQl6EBLI1paEpv3cWWkkbIMBFoiOUU781XisvTBS9SaG30Ylz2XQjDYmGIYtMXUMatgNq0gm68QUzXt7K6mPasE4PkEtYAIEG83s+vVvhC54Hq1v+l1BXOjqlFTrJ4sG116Rx95k/HjTLSvuKW/AN28RVLoqQujDAwQuHudpt6d0s1uvzVAORzjINw7h02gsKEiqfz7EIZCWPcS3OrkaxfSEzbb/z7o4f8BUEsHCKC02fBjCgAAsUgAAFBLAwQUAAgACAATNedAAAAAAAAAAAAAAAAAFgAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNLK81LLsnMz1NIT0/yz/PMyyzR0FSoruUCAFBLBwhFzN5dGgAAABgAAABQSwMEFAAIAAgAEzXnQAAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWztXNty28YZvk6eYocXHbuVoD1jkUrJ6DCZasaOPZabSevRaEBiSSEGAQYAdbDT+7Yvkeai01ykF43zBPF9HiJP0n93AZAgKUq0JFvOJIkNYPff0/99/2EXYDY/ORsm6ETnRZylWx3i4Q7SaS+L4nSw1RmX/XXV+eTjDzcHOhvobh6ifpYPw3Krw41kHG11GBNBt6vluo4Cvc5xGK0Hgd9bF5hroXt+1OuqDkJnRfxRmn0WDnUxCnv6oHesh+GDrBeWduDjshx9tLFxenrq1UN5WT7YGAy63lkRdRBMMy22OtXNR9Bdq9Eps+IUY7LxxcMHrvv1OC3KMO3pDjJLGMcff/jB5mmcRtkpOo2j8hgWjCnvoGMdD45hUT6Dhw0jNQKNjHSvjE90AW2nHu2iy+GoY8XC1NR/4O5Q0qyng6L4JI50vtXBHpOcCl8RKjooy2OdlpUUqUbbqPvZPIn1qevQ3NmxYEplliXd0PSFvv4aSWn+ppji6kqqK3VXTNCauTB3oe7C3QWmcBIXcTfRW51+mBSgmzjt54BL81yU54m2w1UFk2WRNZhyEb8AYYaBAE6ZRo14zfyR8Iebio32GsjUqGU+XnHQekiCibz6mPRaK2XNOn02PyYVF6xTLhnULfxKCxVTuoWh7H/2z9yIbNkyZ0d0z9cbUPK3ssTNjdoUNiv2o+LYyFb0KfWwMPbAAiQCw3uCBBBfIBIg6SOwA0QE4vCsgPg+YqaMI4YUCqCAMMSNRQhTy33bgUSCIMmRFCBKoGuOBEPEWhNHYDyIWlsiiDKQEAIJaOKb3qzlMYm4hCemEIdZgXUiBm3gFsaliBHETDsqTAsfUYmk6Y9wY9FSmS4pkhhJa88cI04QtyOCsELMtAPTR3Z22Ji5va8faaW4OB2Ny5ayesOovi2zUYMKSIPnmXg254laju+DzSTs6gSCwYHBFKGTMDG2YQfqZ2mJaji5Kxvk4eg47hUHuiyhVYG+DE/CB2Gpzz4F6aIe28r2srR4nGflbpaMh2mBUC9LcDPnLCFT97SZNTywqQo+XSGmKuTUvb9w3Axq0LjQMH6WF7V4GEX7RmLiJECTj9LkfCfX4fNRFreXsblh48qmHveSOIrD9HOgrRnF6AVNwozxDHWYEZLVM8ny6OC8ADKjs7/qPAOvRamnhBSBL3ngM2xixrmrYkp4lDBOVcClkhJqil5ozJALD2QFkSwQNJDEhzYXVCk3sj5pEArP9GSxgzxuuGLu94udLImaarv83XBUjnObIIBrzM2attNBoi1FrIlD9O0972ZnB44bzPX19HwET9hNoDuwakfgJKiAlQyqa9ddrYyZWSOFrQy2ErgmWxw19SSgVsJeu+5qpYC9bmrVSkm9SoLrYeLCujbcqcymdluG+yaWj9O4fFA/lHHv+WSppsFn42FXNwxq90lurk8za0grivKLKlEz93+Zun96rMvQJByCQlKmfF/A3zRQyhF1hqKbz3We6qSyCODCOBsXzsCnjCXSvXgIj66iUmlo4P4zLMCVRnqQ63rhiU3enMJtLZ7m+lyx7erTPBvupydPgUszE9jcqGe5WfTyeGQoi7oQT57rCSth7SGEo2i6nTFhUF3PhB1Qb2lUC/2//jYdjJMM7b7+Lyijl6EQ7Y7DKI+T19+WYGUFOIBxeZwBoR7ECegqRAdhHL1+laJIo12d5hnaCbvdcGDGBb8G6BnrT/QQ0jpUWopbK2mg3raZosEUZd0vwbU2cdjVuwd90mgXpBay3tpHmIyOLcaV/pLwXOctjdpuH/X7hS7R2VZnnYH5nRteTWofZtEsCgCyVRX4opEj4Uhrx9+ysls0gsGs2becKcBa2IGI50tMhPB5ALlpQIPADryOPSkYJL9S+oEPFQz2Ay8cbV2ubdRlXEUrurjSGb4AiZ2mLcLDYZhGKLWZx2Or80n8CyGS7MZ5L9HPtiHCH1aqHZd15c5R3/VY9XMJikZ8OY5TSplG0Gb9g+r6xihyq0qqrgkiWQxiOD4zZM/PXX8TlzNBl3rgUziEMYUDyN0U4zW4XHIJjsb3lcK+b7ZTNw7ugR6Y8hl4t0GPpAGyBW54GbhF1WMNXnhFeJfbKRHMxR5zbTAmYinI8zhejgaonSjFZSADDHgwSji1eDAvCIQxQbA+BtZojP+FRQ/wkYJgqYjPVDAbGktI2p7DHhQCjmrIgt3dn+Io0mnjQfRXqWtTuIAVD0fgSeOyASEx/NpPwZ0W2vrf+ajyXOuRSQcepU/zMC3MoUJ7sasZeriAAjsrWfd1fPTNWPg6cQAup8YN+GniCeJz4cM0MbCEKNJYcqAEJRQsXEEKWlHnZi35UQ7BdZClYfIAuLfYoBeh2T3Kl+NpqNzAZaSvb811rnlVLN/IkBcZ7PlFBg5wrPvgT4QCdwubA18JwZaYMq1JwVY35dUssMKnhdnjVSzw8bUAuyETpFVQE7djg1fhA/UwRNEA+5hBBk+lM07uiUDCNo4B6oQTeguW6ZKl7bx3cZRFIa1QbeHcO4qXIw25eNwbhfkEbdPkLhvocmuiF1hTPNDpCSwlywuEznC1MzvHbmboRV1yRqyBmzpSFb0gU3gCvfL4DG3X8tu11DY1cYJ63BcUwjk2p9fgyKGCVWNscyM6n4dvCyMwl4ff1YBeUapFs72jchWHYsTvTEZ3my4DpkMDxgi4C6woJsT4PrNZ8MB/cJ+IAMI5Z0TIpV7DX+w16HLwHsbRaAF+RvnObczB+HAVEB/eBIS4OhAy16tCOAkKTpnrZHlMuApMijIWcEkJhu2S5MptyyHOy8AXABPnvvKNw1+CkliMErkMpTzP8sWO/eEcQrtHL/UR+dsqONVN3pHBTYXwKoLX59FvDBfzOJYACSTIkH0pEYhqf4Wpj30RKKmkDwnaLdjU4t1uY1LWwSZhqZ81LvkZpF9ryGTUzyok1pDD/Bk0W0NV4eHh4Rr63Aaoidyku52mci92701Nke213Qv6PTKHf5NcvmpWTdwcuOwc2n/muLXitvwmNuVvI40HhgZMEKIgjYfoynwpHQ+5Z2M0gXwuoJjK6nQEQrQICKT3BLJ/JfCy/filace7Dd9PwvPZY7fKGTj34mi433+2g375xzcI8sg1BAQBRh1OKDXHE72cJzkMWnNAvyccMVs6wSXmDBy+glwei/rMhvrg9xnGHAusuDseXQ88iBZK8MCHXaDP8ZU2eneTI4tSPD2H+e5KEecOnNi4CL5+3UPZS09sbiQW3dyx+vzpzN5KifmqyMH2MYqdCs2r2KrNvT3wJ/8yfuQ++uXv36HGvdine31bi13dvZ++v6fh7t8umpn4dNQ/vH//ZplxO29VmHl/S0iAFYN/qajOKKgHkAcCMkcIIpL5t/NOJTmH+H7BgYA7DtiFC6sY0LbmcXj0MsrjKg6ETrzrxHtwgZ1qdBlv3PiNzTddXugILzu8fve7wWl1X/JO4tbS6Xce3IgHPktIAYTGgiiyLLapKVu5C6FtOWjd9wk05glqXt1R8CVCchzwak+qFKQevs8kZK8BJy5rlR4NiDLnSQFmUij5qwGt9x6Bhj3GFSGSAg4CthDK2dm67zGFMYDoQ8ZISHVGTImxS4wBNxlQEWDxqwEteo9AYx5jFEMyT7lSivv2Cy37WpbAhpExA6nPqEk6ADSAkmBowH2GAymx/x5h1s4g7Hdhs9vDJorPpgw//8/lCj//4JKFn1+5bOHnH5fnCfYbogZ36MX0CzMc1+ctsAk3uTPhnAWKN+/MrnuuOL9rJFdkztynaYv2cosRDfPeVF5XUzBJstMnup/oM6vyq9rUjOZ++E1zb6i5V7Oag0ycEamIwAEJCIPc/d1obmq76otlHxHdUcX+eFcVeyc0dzbKYRizw2zeer08GHdhzwVVZlfW3oFvXPrOzLW+kQ067LlvYo++YJNuTlEH7tJ1lzd41U+Wvepnq+TQt7w/h9HCkdWuLdtbHnH3+zPhtv3FTXOiD/rdPTyc6BvK9w5d+N3vT14A2KN8B+JU0d7hGlok9c1EatdIQff/mWnYltoxs1hDv/tqnJV/fBzmYaKTbJCHw8wVXT5O1QNINbQBiX9OVjXp337oG0ZV13Xpk2zYnYw2VRZHuiqeP56uBY5e2rtL3pWV+mxiY3NN54yt/aX4W0tj7c85Cp3H/clPH+z3+7xTZ4+1qy3DvLQng8h9UEYVZLC+EAqbhLWOM17AJDdZrcRQ3n6xuQKBp3Gt2Vqz67uGzHvt2p0Jly+UsOxc1Ptew6mfvt/TfSiKns3CdkXOPQFEq2/O27RbTPYFo7g6yLxHuhfXki4/nprAbnsCexdQudXdiymKzzG8nt/Ry3roVUi+qPX7x/MZ9z+1JXq7FrBAm9YJLqKGJfW9RbzcnrOZOdbed0bT7hfNcbhh3+oTa70itrJ1ycSkp2T22jJukrM2gfaL16+KHqizqFm+YGLzFIeqo5cjvQqvmya/kflCMs8npbvQv06qnNRBVHHiD6jWKNxO1yzKVVtIVH2umKm+Pyisg759qYRPA3M2hFUFg+8RiQ0SnApOfBZczae4rztnPylx5r7t7Hn+U63Bcsuwn3U2uh682c9j3u2XnBd9F/12vuSUHiG+YOZDEEDY53zmQ05s3p1wzDjBEsxOScNR8yUnkAMMEbYafsA5EQGmi0/7zC954z6A9Mbc2L2IG8ercOP4N25ckxviMmpcxAzir0aNee8Nbveot9h534McYGAj9HGzyap+WNnONz+b/OKySjjvr+rw3TSu4O/naEQxnyKSIHfKzzPP5wE1P8wKBAnMm1Dj5aXH7JsBRalSgbrYy29M/87V/hq9+r+nfPx/UEsHCBRRTq8mDgAA2kUAAFBLAQIUABQACAAIABM150Dd2rSMiQEAAIQBAAAtAAAAAAAAAAAAAAAAAAAAAAAxZmU0Y2UzMjc2MDUyMmMzMDMxNzZiMzNjNTBkNzkyNlxBQlNUUjE4Qi5QTkdQSwECFAAUAAgACAATNedAhegym/YDAACUBAAALQAAAAAAAAAAAAAAAADkAQAAMTcxNzEzZjM4NzE4MmEzMjgxY2E5MTEyNThhZGU4OTlcQUJTVFJDMTMuSlBHUEsBAhQAFAAIAAgAEzXnQKC02fBjCgAAsUgAABIAAAAAAAAAAAAAAAAANQYAAGdlb2dlYnJhX21hY3JvLnhtbFBLAQIUABQACAAIABM150BFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAANgQAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAEzXnQBRRTq8mDgAA2kUAAAwAAAAAAAAAAAAAAAAANhEAAGdlb2dlYnJhLnhtbFBLBQYAAAAABQAFAHQBAACWHwAAAAA=" language=es /> </center>
| |
| − | | |
| − | ====Ciclando en Lógicas Implicaciones====
| |
| − | En el recíproco escenario dinámico, desarrollado para otro de los talleres de ''Centro Babbage'', se controla recíprocamente, a partir de la condición de cíclico del cuadrado, qué otras variantes de cuadriláteros cumplen condiciones que pueden encontrarse '''''lógicamente vinculadas''''':
| |
| − | | |
| − | <center><ggb_applet width="500" height="600" version="4.4" ggbBase64="UEsDBBQACAgIAHWNfkQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAB1jX5EAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1d247bRpq+zjxFQQMEk101u4p1IJm0M5DbnYkD54B0drDYhtGgqJKaMUXKJGV32zGwl7tPMTMXi72Zvdo3mDzAvMM8yf5VRUqkRB2oVrdbXhuxSyTr+H//uYrMye+vxxF6JdMsTOJHHWLhDpJxkAzCePSoM82HR27n91/+5mQkk5Hspz4aJunYzx91mMU683ZwZdlMNQ4HjzpDNpQBo/TIsyk5YoOhf+QGHj+SmLhyaAfMl34Hoess/DxOvvPHMpv4gTwPruTYf5YEfq77vMrzyefHx69fv7bK0a0kHR2PRn3rOht0EMw8zh51ih+fQ3e1Rq+prm5jTI7/9dtnpvujMM5yPw5kB6lVTcMvf/PJyeswHiSv0etwkF/BWhyng65kOLqCZToUlnmsKk1grRMZ5OErmUHTyqVecz6edHQ1P1bPPzG/UDRbTgcNwlfhQKaPOthixPY8x8OUC+oxQjsoSUMZ50VdUox5XPZ28iqUr0236pcekQgAIMzCfiSB5H6UwZrCeJgCPWfXWX4Tyb4PY+bpFK7n0yFdGx6Hb6AuwYCbocGjzhHrwn8udrvcKZZeHbMypOmxxYjleEx48/Fg8K76K+AvUxNZGBHmkCdJpHvE6JdfkI1tjLqqIKawoRDCPMLmHqamsE3BTMFNHWaaM1OVmTrM1GG0DU2LGw1LJKTFEu3b4EhnQ3rO8pA2bx7SrVCVKKr9gogily4oUoQimmCqYMWlMJeOLgg2BSkeuuofT12sY0sz+60oyCtMCavQ/+m/S4uh6wi4OOJKrmwxoGD3vUSGFbp7XqRrd0ENdV3CGsd0cKPomZIUZRvS706Jk+NS/50UM0LZlapb6KBcjjM1R+ohrnmQIA5MzRHxkHCQoxjbRoQjBrdckHQHUcXGDFHkIg9uEIq0CuDqKXN0HwJxggRDDkbCiAKiDHGKiFYdDAEBkFY/QA6bQg3OEYdWjurQVn1QgZiAK+oiBnNTmsdRwkahIVzD+DaiBFHVmDjIFkio/ghTGk24atrQpY0ETEGTHJQXKC6jtKC+iyhX6q+DJkkWzqh6JaNJSRxNvzCeTPMazYLxoPyZJ/XKgyR48XhG4gI16Wf57AKqgW2aW8AGe/gsjEI/9lvYRJfynczgLUzSTHkK4R6ESdq0wPdhkZbGrJikBqquMklr3ZmPduOjtrw/bamohfxrmc1QGKU6rplpv200arX23lRqC31qE2LvplEPNbAQ5DC0+PsILHY2jaQpWlulxD+q1I8q9QGr1E9q1xrOyO/LKIxH54pLEHrlR0pu9AjDJM5RySDM3Bul/uQqDLJzmefQKkM/+6/8Z34ur7+C2rPV6aF1dulEToMoHIAv/EfgIE0K6BDNkk1KuspkExfUjBIkSTo4v8mArdD1v8k0gTkRbHnVPx10Y55Q7KjEWxb4SgaYV6+mBOSmeMaxhat/inXKV7PVNCBkyK9+P80eJ9Ecs0kSxvmpP8mnqU4WAuypWkcvHkVSk1PfC65k8KKfXJ8bOlLT1083E7jCZgL90WkSJSkCEbU5mKxRUfZNqeuomc1qYV0H6xq4BCYczJ4Tz9Y1dNk3pa4FSJupFSsl5SoJLocJM61YFEWrnKX5RFnYaRzmz8qLPAxeFEstGnw3HfeBxWZsCxWehCblaNKr9WFI22HIwjBFu8ZxTo4XmO/khUxjGRkWiwHyaTLNDM/P+PaTk2kmf/Dzq148+FGOQKJ/8JU6zWE4U1WvzMigDMIxNKyJja/w/xeYvrk7kKNUFvX9SKdxDQL6Ka4y/NJt3dVXaTJ+Gr/6CZhrYaonx+V6TrIgDSeKh4GC8Wjqj4AKMgPwQdm/kHOmHYSZD7ZiUO0FSJHBmgKlvYCQuSLz0/EkCgM/CH/93xidh/nUH/hIxiiAH2kY/foXIEcC/fvT/CpJZ+EuOvfDgWoykOhUxmmCHvv9PswGRgYlAVgqjRDJMbhkKNcyEE/HMg2DGfR+evk2SN5pRw+WOy0oMmMdrUmT/s+gw2Ym1LSc4wKPlyQKz+QJ+dHkylcuIimkwr+RaY3wusfvh8NM5ugafDcVmt9A6VQef5sMyrkVM4uU64nGYaxHG/vXml39fpZE01yeB8AH8Ty/b+Ze6EGKlQ6DBjYoMKwHo3o/YRhey5kWAlKHb4Bx61w4F+ocVPMLcGxBLsAiGfra2Pz6OhwMZDybrB8D52rEQctOjFxNpDQimRfaCU2ANFq5VcTDn14rsNObujSAsBlclxDWinKG0uPLt12D7mokK6NVocQrgcRrgZwjhbdePGlevBbUTANlUcMT2OJA7DcVFtULVvreDEqrdxdkfFuq9T4Aih3ZlrNnkgXJeOzHAxRrf/eHJLoZJXFn7kz5WJEO+aTkO+TbKvQxhJrmZR1Qa6aWb2r0oaBwGwoGKhwK/qhzCoV41HliJlEM3YCbmUSJjOp6pZSyiqw1CGlrvHXEOyrKlupuAfPVnJnJkbqaa+zdeHP9XNvyZ7NSqrIfLvQqV+UbJcBuzRvEdI063QCUfBmbJpnxUkJtPsN8xmiRkounsXIipDa0y27HCyknyi38Pv4p9eNMbTRvq2EXEekfBiJHrO6rq3Tpjd5MZ9j1bOy5EIAKW5wdkUJdEIvVvfsPBrLgNgq+Gi3cKWCu5brEcRnxHIyBTWwDjdLpM7GyLVLDaCn0OFiMBoeAES/U3CqslBhRix8sKHW/6HQ3SFRWYGSKvinuEBHwFBcNTaHm6EJG446dyCcHQCxwEkXdKKygFr8TB1KRq+4+9pecxbNNDmCV5mf3b4rncSuxNe0IXwvKfoKhJhaH22wtTKIZJns9TOeFXm7088+W8MrX47Wo5fMdEWvIua1DjKzDpCYPXs1tVYbWruuN1arc3pAFuANtXYfqNEyDSG6MyJZBG64HLUjiSs5ouBtks2Qr4UUqdf+abafkjAxHMn4F60jSDKFrXBxMvcFFFPOmvHNNdDStnpHi1htSETcQ7DS8Rr2yfq+s1bNVNsviatdu9gfEvEeLIXpM76HWpVrtL/a4HtL16k+afQO11RAOAam1TNJLgwUOGZayrLmjt8QdfnoZbMEgEz/Nq4nFHZ3sdSnElnzSyA68ZAf6/4gd7kH5NJnzknNq7PTNpd/GpqvquzESZlVGwtu7UpVcNHGLgOuujTq2PEq5EJg5mApquyYJDsEDc5lr247wHBdzZ62F580Wnq5HTkMd+fmi5TgzeuGPWhYutAHpot7zZRftU3+SZF+0ctSKJkvA1nem7tRfO7KZcXb37kQ72/lju7nN34ZpmqQLUJXWnajNoVhe9LrobBmox+2BenwroPaXEd8CBnUIybEJZgSEiKoD4m4hQiA4mDged4XH1Ub0/kGZadVm0/qjf3NRULKLFuVpGac/mFZftwHqD+9BlnaB6Tv/O42KLt+Y8q5C8K93pMn9xuA1vlXBBmfNfHs3QXjTLk4p9QUbmqhhrjzqAV8amnovTL3I7OaMNzFvfeNG9bLSZSMbPPj9+phc7QNH0U+l3b7y8+BKnzPRJzfM9fz4A98LR2yfF31x397QjpsNjdsKN5p/CWNC2K7rcGJT4cIjaqJtqs7luzbm0MbxPCL0o9W+/CbGeGAp7egQoCMKuaraKbYcbAvcUMeF29Qr3FAPHB/HcQQhzAPcXPfDgWp8CFAdLWFlF55nBSrheq6B66iOl2AHhdeCwzVcDjXVSSb06Sj/AmFjkZ4OL57IIaxucAH25XkX0S6ynxsztfSM6GeL1i1db8YWz1OliyepaAn7Kre4mgYja5FvF3org7oceU/aRd6T9xh5s8JcrA/P9nNShtg2RNyCMUJcVkZvwuEY5ARuE2I7dH3kvVtuvTGWU2TX7JsvAfj4krQK3qD6bh5wOwS3zK5ji3pMbZM6xLOZIG5xQIlYQjBPuNyxbZc6+C4o3byLUQmbDRQXoBZKTfKP//wTwl0EcKh/fFAR+bJ+GGxCZGlbuwmTNj5rueVhq22fuzUuhFCXuerTAcRxXWYyUoCigxmnlINrRwEx5hQnfBzhUSzgic1dj607ibApB/tekpUFlHWBayVuG4BtPjLbNgAnjeqy2AK8c2Wp1GINfVowBec1XrmLzNeKWLW2e3Fm2l681WL75B0YdXSEqpb+uYlPl7c5gql/+XaQhoVCkKbDK1M9NIcTf24X1c67XCkKbQ4ltsi56bfhmt2LfZ9IlLtmnjjVU+Vki/3AtSZmQZs1W3liOa4gnGAVk9qEFFmWoyV9pjmXWR6YfwwVMYWqZN2+7wYI7z12uToMQIDwtOZhFVstzGI1d4yUpxHhyhU2YOi5lNziTNW9AxIeBCDUsumix1ucH4eY0SGUQ4gPU8IGENeCWoQCbAwT4bi3ONB774D8fBCArPLA+KLGMolhYRFBXSI8TjzPZYSeHT0wIbmepDC0ckAKMkOgAzeLPasF062dbrDf6XO1SYL+8R//hXS1x2prCy7/G21qdVZp1euix6ZVEQlsGg6c/7LmvC3AeKEzwRdncE9V7CIC4oFd0+J3ICvon9Df//0z80JonQv7SRJJf+4dTBaTBRXC3urlk52P1qxH62WB1m0ouEXbs3rbs1nb32078J/rjT8zrf/218lWsLxchGXutz9EVJL3IEM7INGbI7FfKUoOTIriAq9yB0mBMTQLx5o8swe9VQ/WUH1Fg/mDbUgaP2iS7nTm8XQp3ButD+XqZx5HDzln85CPubmW8ET1LPnGY268OOZGLG/xDHrjxsOqU48N3kaaTJJYXpJCAj99OU3yL1IZIJmh4Nf/CaIwSMzNzrKQ5PJ67kDOu9qaL4ChBqHJvkD174va8Won04iMvtqVZfRHJTKZhsP5R1jCN/LbAiHztQncKUlZ5hxyP811hgyZlA+rvWNUxAXcEqwKHK1mfLYD4m18Sd4tgREnu+NherwlJn/7awMqe9zZa4kKXYEK5jVUWImKqKJir0KlrkULi7KgRt8a4gMa0+JjBP6gAKSLqs8AtvzXv8SjadT8OBn3k3Ag688MznFYba0u6wO9m23lTfQeHfxIusjWP17qHT32vOEIFfR5qV4GXqvjayxUtrhN1u2WVm4J5CNqebX3ZsvjqNgS2wG7Q8507k5sypRaBTi+Uqn6TW79Q73LrX+Afpebd6yaU6bWnnKm27so7VOm8/Q7M68B2mti/haveO+6RfQxo3pXr3gfDCI2XjgtbjZYqRCMUo/b4IwJhxhEOCAC3hkTrvBcxmebR4eASHAYiDCLNAFCLVE/7F+ep8LcJZgTkCqMGTkgPFq5wh9Tqnd0KGrzKfQnoXrR4+K0i4C+ROV3ZgfS1Ve0ip9LR9SfF6emlnfIv9pk3qs75F8dwoFs2wJ5dCAQZZ6wqf5Ys3mbQ+Cqw+3u5w3y5eAo8uPLt7lM6pHRKQQNaRKpbxCCi6w+EBZWvxqWqSupHGqIxyG08CM1gFT/04yBP5Cpj8C3Tj7/9LcEf+F/hs5DGQ8SFIQyzRNkTnabf2VU/+yY6rLq3leqdlGkH+tON/Uxi+cq9XTDfuvZlNFEbSq6r2I+u04l2DCViZ/6kYySUeqPV/bURW3IsoK0W0a9c1ZZr3ubT57cXcxSSwy4rDxATGsJHboyhFmdMbBrMlHECu+KgBL9MyqCOPhlbhV0bMh5NqYP7N1smLJdOoCwb0vLvSRsFAJLn28wuQG+UoO1Oytlsq69NChtxI9JruxKr4uOdCrfAUfTFo4HllaILtK1nje+Pfi0jQF5+iDectrDOSrwQ4TrCuZwmzLH5aT88IYNZsdhDqEekM/ez2dKdsqYP11CKmuTMc92PXlaezXn3j4S8GDS5dgFh5OD/II7qo9gbPlWOMR4HsXM8xjnjuAci3bp8jYyf6pci/QiA4F+2ijT37SR6W8+FJkGvUspgwACdB53bVB9xRdhLA88Std2Qf3agtN7OxpZCnUp0Do1901jOi8wVYdlJm9UZvKuykxeuEsmL1idxLP3ffBxttnWYIbv6OjjcOcD9h9S2LsByXvPRYwOBRVqQZgJ6ssBrYHVoelZvo5D+AnuAXY45tQpXojAlgMTpMJzCFFHINfl6x4aJlcHggkEKbYgHgFZUdbV88ozqRxTF4wqiBDFlOHiXWxhMUBNCE+4BLw25hwQJOHBQMLcuvnULxyIuqnVeDgWSAzF3IUAVDV5WFpri3e/eqve/Oq1/3RHb9WnO/b9LevtP6627y9SH1e/pq+uy/9365f/B1BLBwiwGRY/NhIAAGt2AABQSwECFAAUAAgICAB1jX5ERczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAHWNfkSwGRY/NhIAAGt2AAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAzhIAAAAA" language=es /> </center>
| |
| − | | |
| − | ===Considerando la Construcción de Tangentes a una Circunferencia===
| |
| − | Repasando uno de los métodos para trazar el par de tangentes a una circunferencia desde un punto exterior y teniendo en cuenta que además de las [[Herramientas|herramientas]] disponibles se puede apelar a cualquiera de los [[Comandos|comandos]] que aparecen en el listado que se despliega a la derecha de la [[Barra de Entrada]], es posible encontrar una nueva estrategia para la construcción del cuadrado.
| |
| − | | |
| − | ====Pasos de Construcción====
| |
| − | En esta ocasión, en lugar de hacer uso de las [[Herramientas|herramientas]], se realizará la construcción anotando lo necesario en la [[Barra de Entrada]] como si de tratara de una situación en que, por algún motivo, no se pudiera contar con el ratón o ''mouse''.
| |
| − | | |
| − | {|border="1" cellpadding="15" col width="470"
| |
| − | |1||A_p = (0, 0)||Punto A {{hint|1=El subguión permite establecer a '''''p''''' como subíndice de '''A'''}}
| |
| − | |-
| |
| − | |2||(3, 0)||Punto B_p {{hint|Si no se especifica un nombre para el punto, se irán nominando en orden alfabético.}}
| |
| − | |-
| |
| − | |3||c = Circunferencia[A_p, B_p]||Circunferencia con centro en A_p que pasa por B_p {{hint|La circunferencia es in objeto dependiente}}
| |
| − | |}
| |
| − | | |
| − | {{note|GeoGebra distingue entre [[Objetos libres, dependientes y auxiliares|objetos libres y dependientes]]. Mientras los libres pueden modificarse directamente sea empleando el ratón o '''''mouse''''' o el teclado, los dependientes se adaptan a los cambios que afecten a los objetos de los que se derivan sea que se los afecte o cree a través de uno u otro medio (ratón o teclado).}}
| |
| − | {{OJo|1=Los puntos que se establecen en un objeto, siendo dependientes, conservan el grado de libertad correspondiente y pueden desplazarse con el ratón o ''mouse'' o teclado a lo ''largo'' (si se tratara de una recta, curva, cónica....) y a lo ''ancho'' del ámbito (sea un polígono, región delimitada por inecuaciones, cuadrante, etc.) en que se originen.}}
| |
| − | ===Desafíos sobre los Objetos===
| |
| − | Si se [[Herramienta de Elige y Mueve|selecciona]] un objeto, sea en la [[Vista Gráfica]] o en la [[Vista Algebraica|algebraica]], con un doble ''clic'', se puede modificar, sea su definición o sus datos usando el teclado y finalizando la operación pulsando la tecla {{KeyCode|Enter}} (o {{KeyCode|Intro}} en otros teclados).
| |
| − | Los objetos libres y hasta cierto punto algunos de los dependientes que conservan grados de libertad, se pueden desplazar empleando las teclas de flechas. {{Example|1=Se pueden desplazar los puntos libres hacia arriba y abajo o a izquierda y derecha con las teclas de fecha correspondientes.}}
| |
| − | {|border="1" cellpadding="15"
| |
| − | |4||C_p = (5, 4)||Punto C_p
| |
| − | |-
| |
| − | |5||d = [[Comando Semicircunferencia|Semicircunferencia]][B_p, C_p]||Semicircunferencia entre B_p y C_p
| |
| − | |-
| |
| − | |6||E_p = [[Comando Interseca|Intersecta]][c, d]||Punto E_p de intersección entre la circunferencia y la semicircunferencia
| |
| − | |-
| |
| − | |7||tan_1 = [[Comando Semirrecta|Semirrecta]][C_p, E_p]||Esta es una de las tangentes que desde el punto C_p pasa por el punto E_p de la circunferencia en juego.
| |
| − | |-
| |
| − | |8||sr = [[Comando Semirrecta|Semirrecta]][C_p, A_p]||Esta es la semirrrecta desde el punto exterior al centro de la circunferencia.
| |
| − | |-
| |
| − | |8||[[Comando Refleja|Refleja]][tan_1, sr]||Con esta maniobra de reflexión, queda trazada la otra tangente así como el punto de tangencia sobre la circunferencia.
| |
| − | |}
| |
| − | [[File:Tan 1.PNG|280px]][[File:Tan 2.PNG|220px]]
| |
| − | ===Construcción Controlada y Mejorada===
| |
| − | *Para corroborar, al menos de modo preliminar, que la construcción de sendas tangentes es válida a nivel general, conviene realizar...
| |
| − | **la prueba de arrastre de cada uno de los elementos en juego para verificar que todos mantiene relaciones adecuadas
| |
| − | *Para mejorar el aspecto del boceto, se puede apelar al cambio de propiedades de los objetos a fin establecer...
| |
| − | **con pistas visuales cuáles son los elementos auxiliares y cuáles los que se desea destacar (reservando el punteado para los auxiliares, por ejemplo....)
| |
| − | **empleando el contraste en los colores, grosores de trazo y estilo para mejorar el diseño general
| |
| − | *Para evitar la superabundancia de referencias en la [[Vista Algebraica]], establecer algunos objetos como auxiliares y conservar la opción que fija que no se expongan
| |
| − | *Recurrir a comandos toda vez que esto evite la proliferación de trazados auxiliares con herramientas. {{hint|Hay opciones de comandos que no están disponibles en forma directa con herramientas o que requieren una secuencia de maniobras que pueden, en cambio, sintetizarse a través del ingreso adecuado en la [[Barra de Entrada]].}}
| |
| − | *Para aprovechar el mecanismo de esta construcción, basta con establecer...
| |
| − | **sobre la semirrecta que pasa por el centro de la circunferencia desde el punto exterior original, uno que esté a la distancia necesaria como para que conforme, con los radios que unen el centro con los puntos de tangencia, la diagonal del cuadrado que se procura<br>[[File:Tan3.PNG|450px|center]]
| |
| − | **unir este punto con los respectivos de tangencia y el centro como secuencia de vértices del [[Herramienta de Polígono|cuadrado en marcha]]<br>'''[[File:Tangente 1.PNG|420px|center]]'''
| |
| − | | |
| − | ===Cuadrática Polinomial Deslizada===
| |
| − | Si se ingresa en la [[Barra de Entrada]] '''x^2''' y se pulsa {{KeyCode|Enter}} (o {{KeyCode|Intro}} en otros teclados), aparecerá en la [[Vista Gráfica]] una función cuadrática.
| |
| − | Si se la selecciona, al pulsar las teclas de flecha, podemos notar que se desplaza su representación y se modifica la formulación correspondiente en la [[Vista Algebraica]].
| |
| − | Una exploración sistemática permite esclarecer la relación entre estos intentos y sus consecuencias. Se puede registrar, por ejemplo, el efecto de pulsar:
| |
| − | # {{KeyCode|↑}}
| |
| − | # {{KeyCode|↓}}
| |
| − | # {{KeyCode|← }}
| |
| − | # {{KeyCode|→}}
| |
| − | *El desafío es establecer cuál es el impacto de cada una de estas maniobras sobre...
| |
| − | **el gráfico
| |
| − | **la fórmula
| |
| − | *Redefinir la función ingresada, con un doble ''clic'' sobre su registro en la [[Vista Gráfica]] o en la [[Vista Algebraica|Algebraica]], anotando ahora '''3 x^2''' y reintentando las maniobras previas para re-indagar su efecto.
| |
| − | ====Hacia la Polinómica Deslizada====
| |
| − | Antes de pasar a cambiar el registro algebraico de la representación de la función, pasamos a crear tres deslizadores que harán las veces de coeficientes de la versión polinómica.
| |
| − | {|border="1" cellpadding="15" col width="500"
| |
| − | |1||a =1||Crear la variable a = 1
| |
| − | |-
| |
| − | |2||||Exponer la variable '''a''' como un deslizador en la [[Vista Gráfica]]. {{hint|1=Se puede Con un ''clic'' derecho (en MacOS: {{KeyCode|Ctrl}} + ''clic'') sobre la variable en la [[Vista Algebraica]], se puede seleccionar '''Muestra Objeto''' en el '''Menú Contextual''' que se despliega o pulsar en el redondelito a la derecha del objeto en esa [[Vista Algebraica|cista]].}}
| |
| − | |-
| |
| − | |3||<small><small>a x^2</small></small>||Dar doble ''clic'' sobre la función para redefinirla como '''a x^2''' y pasar al tipo de registro algebraico polinómico. {{hint|La '''a''' y la '''x''' (es decir la expresión '''x^2'''), debe estar separadas por un espacio o por el asterisco '''*'''.}}
| |
| − | |-
| |
| − | |4||[[Image:Mode slider.png]]||Crear un [[Archivo:Mode slider.png|deslizador]] '''b''' con la [[Herramienta de Deslizador|herramienta correspondiente]].{{hint|1=Una vez activada la herramienta basta con un ''clic'' en la [[Vista Gráfica] y, aceptando los valores por omisión, pulsar el botón ''Aplica''.}}
| |
| − | |-
| |
| − | |5||<small><small>a x^2 + b x </small></small>||Dar doble ''clic'' sobre la función para redefinirla como '''a x^2 + b x'''. {{hint|GeoGebra reescribe la función si en lugar de redefinirla se anota la nueva formulación, con el mismo nombre, digamos '''''f''''', en la [[Barra de Entrada]].}}
| |
| − | |-
| |
| − | |6||[[Image:Mode slider.png]]||Crear un [[Archivo:Mode slider.png|deslizador]] '''c''' con la [[Herramienta de Deslizador|herramienta correspondiente]].{{hint|1=Esta vez, conviene pasar a la pestaña '''Deslizador''' de la '''Caja de Diálogo''' de la herramienta para establecer como orientación la '''Vertical''' en lugar de la '''Horizontal'''. Otro tanto puede hacerse con '''a''' y '''b''' además de cambiar sus colores en el [[Cuadro de Propiedades|caja de diálogo de propiedades]] de uno y otro [[Herramienta de Deslizador|deslizador]].}}
| |
| − | |-
| |
| − | |7||<small><small>a x^2 + b x + c</small></small>||Dar doble ''clic'' sobre la función para redefinirla como '''a x^2 + b x + c'''.
| |
| − | |-
| |
| − | |8||<small><small>a x^2 + b x + c</small></small>||Arrastrar, desde la [[Vista Algebraica]] el registro de la fórmula de la función hacia la [[Vista Gráfica]] como para acomodarla bajo cada uno de los deslizadores, tal como se ilustra en la figura.
| |
| − | |-
| |
| − | |9||<small><small>a x^2 + b x + c</small></small>||Llevar adelante las maniobras que permitan establecer las raíces reales en el gráfico (de tener raíces reales la polinómica), el vértice, la tangente en el vértice y en cuadrilátero conformado por estos puntos, tal como se ilustra en la figura.
| |
| − | |-
| |
| − | |10||<small><small>a x^2 + b x + c</small></small>||El desafío es encontrar los valores de los coeficientes de la polinómica de modo tal que el cuadrilátero determinada sea el dibujo representativo del cuadrado.
| |
| − | |}
| |
| − | | |
| − | '''[[File:Cuadri cuadrática.PNG|center]]'''
| |
| − | | |
| − | ===Cuadrileteando===
| |
| − | <table border="1">
| |
| − | <tr>
| |
| − | <th>Nº</th>
| |
| − | <th>Nombre</th>
| |
| − | <th>Herramientas</th>
| |
| − | <th>Definición</th>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">1</span></td>
| |
| − | <td><span style="color:#006400">Punto A</span></td>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">2</span></td>
| |
| − | <td><span style="color:#006400">Punto B</span></td>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#FF7F00">3</span></td>
| |
| − | <td><span style="color:#FF7F00">Punto C<sub><font size="-1">a</font></sub></span></td>
| |
| − | <td><span style="color:#FF7F00">[[Archivo:Mode point.png]]</span></td>
| |
| − | <td><span style="color:#FF7F00">Punto sobre Segmento[A, B]</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#FF7F00">4</span></td>
| |
| − | <td><span style="color:#FF7F00">Punto C'<sub><font size="-1">a</font></sub></span></td>
| |
| − | <td><span style="color:#FF7F00">[[Archivo:Tool Rotate Object around Point by Angle.gif]]</span></td>
| |
| − | <td><span style="color:#FF7F00">C<sub><font size="-1">a</font></sub> rotado por el ángulo 90°</span></td>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#000000">5</span></td>
| |
| − | <td><span style="color:#000000">Arco arc</span></td>
| |
| − | <td><span style="color:#000000">[[Archivo:Tool Circle Arc Center 2Points.gif]]</span></td>
| |
| − | <td><span style="color:#000000">ArcoCircunferencia[A, C<sub><font size="-1">a</font></sub>, C'<sub><font size="-1">a</font></sub>]</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#FF7F00">6</span></td>
| |
| − | <td><span style="color:#FF7F00">Punto D<sub><font size="-1">arc</font></sub></span></td>
| |
| − | <td><span style="color:#FF7F00">[[Archivo:Mode point.png]]</span></td>
| |
| − | <td><span style="color:#FF7F00">Punto sobre arc</span></td>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#000000">7</span>
| |
| − | <td><span style="color:#000000">Semirrecta e</span>
| |
| − | <td><span style="color:#000000">[[Archivo:Tool Ray through Two Points.gif]]</span></td>
| |
| − | <td><span style="color:#000000">Semirrecta que pasa por D<sub><font size="-1">arc</font></sub> con dirección Vector[B, D<sub><font size="-1">arc</font></sub>]</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">8</span>
| |
| − | <td><span style="color:#006400">Punto D</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]</span>
| |
| − | <td><span style="color:#006400">Punto sobre e</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#FF7F00">9</span>
| |
| − | <td><span style="color:#FF7F00">Punto D<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#FF7F00">[[Archivo:Tool Midpoint or Center.gif]]</span>
| |
| − | <td><span style="color:#FF7F00">Punto Medio de B, D<sub><font size="-1">arc</font></sub></span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#FF7F00">10</span>
| |
| − | <td><span style="color:#FF7F00">Punto A'</span>
| |
| − | <td><span style="color:#FF7F00">[[Archivo:Tool Reflect Object in Point.gif]]</span>
| |
| − | <td><span style="color:#FF7F00">A reflejado en D<sub><font size="-1">a</font></sub></span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#000000">11</span>
| |
| − | <td><span style="color:#000000">Semirrecta b<sub><font size="-1">2</font></sub></span>
| |
| − | <td><span style="color:#000000">[[Archivo:Tool Ray through Two Points.gif]]</span>
| |
| − | <td><span style="color:#000000">Semirrecta que pasa por A' con dirección Vector[A, B]</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">12</span>
| |
| − | <td><span style="color:#006400">Punto C</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]</span>
| |
| − | <td><span style="color:#006400">Punto sobre b<sub><font size="-1">2</font></sub></span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006666">13</span>
| |
| − | <td><span style="color:#006666">Cuadrilátero cuad</span>
| |
| − | <td><span style="color:#006666">[[Archivo:Tool Polygon.gif]]</span>
| |
| − | <td><span style="color:#006666">Polígono A, B, C, D</span>
| |
| − | <tr valign="baseline">
| |
| − | ;
| |
| − | <table border="1">
| |
| − | ====Chiquicientos_1====
| |
| − | <small>Liliana Saidón de Cenro Babbage</small>
| |
| − | <tr>
| |
| − | <th>Nº</th>
| |
| − | <th>Nombre</th>
| |
| − | <th>Herramienta</th>
| |
| − | <th>Definición</th>
| |
| − | </tr>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">1</span></td>
| |
| − | <td><span style="color:#006400">Punto A<sub><font size="-1">a</font></sub></span></td>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]
| |
| − | <td>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">2</span>
| |
| − | <td><span style="color:#006400">Punto B<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]
| |
| − | <td>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">3</span>
| |
| − | <td><span style="color:#006400">Recta r<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Line through Two Points.gif]]
| |
| − | <td><span style="color:#006400">Recta que pasa por A<sub><font size="-1">a</font></sub>, B<sub><font size="-1">a</font></sub></span> sobre la que se trazará el primer lado del cuadrilátero en marcha
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#993300">4</span>
| |
| − | <td><span style="color:#993300">Punto A</span>
| |
| − | <td><span style="color:#993300">[[Archivo:Mode point.png]]
| |
| − | <td><span style="color:#993300">Punto sobre r<sub><font size="-1">a</font></sub></span> que será el primer vértice del cuadrilátero en marcha
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#CC6600">5</span>
| |
| − | <td><span style="color:#CC6600">Número l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub></span>
| |
| − | <td><span style="color:#CC6600">[[Archivo:Mode slider.png]]
| |
| − | <td><span style="color:#993300">Número expuesto como deslizador que establecerá las unidades de longitud del primer lado
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">6</span>
| |
| − | <td><span style="color:#006400">CajaDeEntrada Longirud</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Insert Textfield.gif]]
| |
| − | <td><span style="color:#006400">CasillaEntrada[l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub>] en que se puede ingresar el valor que tomará el número y determinará la longitud del primer lado,
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#993300">7</span>
| |
| − | <td><span style="color:#993300">Punto B</span>
| |
| − | <td><span style="color:#993300">[[Archivo:Mode point.png]]
| |
| − | <td><span style="color:#993300">Traslada A por l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub> VectorUnitario[r<sub><font size="-1">a</font></sub>]</span> de modo de establecer el segundo vértice del cuadrilátero en marcha al fijar una distancia desde el primero...
| |
| − | * acorde a la longitud que se ingresara en el campo de la casilla de entrada...
| |
| − | * entrada que da valor al número correspondiente l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">8</span>
| |
| − | <td><span style="color:#006400">Semirrecta a<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Ray through Two Points.gif]]
| |
| − | <td><span style="color:#006400">Semirrecta que pasa por Traslada[A, Vector[l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub> VectorUnitarioPerpendicular[r<sub><font size="-1">a</font></sub>]]] con dirección VectorUnitarioPerpendicular[r<sub><font size="-1">a</font></sub>].
| |
| − | Esta semirrecta parte del punto que se traslada sobre el vector perpendicular al primer lado una distancia igual a l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub> con la dirección y orientación de tal vector. Esto permitirá colocar la semirrecta del lado opuesto al primero, a una distancia tal que permita un cuadrado o, mayor, para un rectángulo, por ejemplo.
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">9</span>
| |
| − | <td><span style="color:#006400">Punto C<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]
| |
| − | <td><span style="color:#006400">Punto sobre a<sub><font size="-1">a</font></sub>. Es decir, sobre la semirrecta recién trazada, </span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">10</span>
| |
| − | <td><span style="color:#006400">Arco e</span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Circle Arc Center 2Points.gif]]
| |
| − | <td><span style="color:#006400">
| |
| − | ArcoCircunferencia[A, A + Distancia[A, C<sub><font size="-1">a</font></sub>] VectorUnitario[r<sub><font size="-1">a</font></sub>], C<sub><font size="-1">a</font></sub>]
| |
| − | | |
| − | Es el arco que permite colocar un punto para '''''inclinar''''' la semirrecta sobre la que se quiera establecer el tercer vértice del cuadrilátero en marcha.</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">11</span>
| |
| − | <td><span style="color:#006400">Punto D<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#006400">[[Archivo:Mode point.png]]
| |
| − | <td><span style="color:#006400">Punto sobre e.
| |
| − | | |
| − | Este será el punto para '''''inclinar''''' la semirrecta en que se ubicará el tercer vértice del cuadrilátero en marcha.</span>
| |
| − | | |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006400">12</span>
| |
| − | <td><span style="color:#006400">Semirrecta b<sub><font size="-1">a</font></sub></span>
| |
| − | <td><span style="color:#006400">[[Archivo:Tool Ray through Two Points.gif]]
| |
| − | <td><span style="color:#006400">Semirrecta que pasa por D<sub><font size="-1">a</font></sub> + l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub> con dirección VectorUnitario[r<sub><font size="-1">a</font></sub>]
| |
| − | | |
| − | Esta es la semirrecta que puede '''''inclinarse''''' y sobre la que puede deslizarse luego el tercer vértice del cuadrilátero en marcha.
| |
| − | </span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#993300">13</span>
| |
| − | <td><span style="color:#993300">Punto C</span>
| |
| − | <td><span style="color:#993300">[[Archivo:Mode point.png]]
| |
| − | <td><span style="color:#993300">Punto sobre b<sub><font size="-1">a</font></sub>
| |
| − | Este es el punto que determina el tercer vértice del cuadrilátero en marcha,</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#993300">14</span>
| |
| − | <td><span style="color:#993300">Punto D</span>
| |
| − | <td><span style="color:#993300">[[Archivo:Mode point.png]]
| |
| − | <td><span style="color:#993300">Punto sobre Segmento[C<sub><font size="-1">a</font></sub>, Traslada[C, Vector[-l<sub><font size="-1">ado<sub><font size="-1">1</font></sub></font></sub> VectorUnitario[r<sub><font size="-1">a</font></sub>]]]],
| |
| − | Este es el punto en el segmento sobre el que se ubica como cuarto punto vértice del cuadrilátero en marcha, de modo que...
| |
| − | * en uno de los extremos establece un lado igual al opuesto, el primero, de longitud fijada por el número-''deslizador'' acorde al valor ingresado en el campo de texto
| |
| − | * en el otro, coincide y se superpone a D<sub><font size="-1">a</font></sub>.</span>
| |
| − | <tr valign="baseline">
| |
| − | <td><span style="color:#006666">16</span>
| |
| − | <td><span style="color:#006666">Cuadrilátero cua</span>
| |
| − | <td><span style="color:#006666">[[Archivo:Tool Polygon.gif]]
| |
| − | <td><span style="color:#006666">Polígono A, B, C, D.
| |
| − | <h4>¡Este es el cuadrilátero, finalmente!</h4>
| |
| − | <h4>''''' ¿Cómo lograr que resulte cuadrado... '''''</h4>
| |
| − | '''''.... el dibujo representativo? ¿o rectángulo, o rombo, o trapecio o trapezoide, desplazando los puntos adecuados?'''''</span>
| |
| − | <tr valign="baseline">
| |
| − | ;
| |
| − | | |
| − | === Variante con Transformaciones ===
| |
| − | <center><ggb_applet width="500" height="273" version="4.4" ggbBase64="UEsDBBQACAAIAO8j4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAO8j4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VvrbtvIFf6dfYqBfvRHYUtzJ5nKWcgOFg3g7C7qdFF0UQQjcizPmiK1JGVL6fadCvQN2hfrmQslSlbkyEk2TpDAMsmZM3Nmzvedy1DO8NvFNEc3uqpNWZz0SB/3kC7SMjPF5KQ3by6P4963z74ZTnQ50eNKocuymqrmpMetpMlOepeCEozx+JgTfHnMxWV6PNYkPqYJHccq4SxLsh5Ci9o8Lcrv1VTXM5Xqi/RKT9V5marGKb5qmtnTweD29rbfquqX1WQwmYz7ixomgGUW9Ukv3DyF6TYG3TInTjEmg7+9PPfTH5uiblSR6h6yW5ibZ988Gd6aIitv0a3JmquTXozjHrrSZnIFexIR76GBFZqBQWY6bcyNrmFo59HtuZnOek5MFbb/ib9D+Wo7PZSZG5Pp6qSH+0RGOEpo+yE9VFZGF02QJUHnoJ1teGP0rZ/W3jmNRPbQjanNONdgcpXXsCdTXFZgz9Vz3SxzPVags6nm8LxeDjmi0G3egCxg1UPeBie9Y34EP2CDo9XWuzo7Kv2MB2hs9UnZ0QfKj+xHwofbhWxphDU0ZZm7GTH67TdEMcXoyF6Iv1C4SOm7sG/DzF+ov3B/EV6G++Hci3Ivw70MZ4fYNDTs2CIhybtvkb6HUdlKIxN3NVKxWyOje7bpVbwDjkR0cARN7sd97iiU/ACFe8x6j8bhoPWTYSANqq+sbDBro6e1pRFLkEgsGwgSQBmBSIJkhCKKgCCICMShKQZGRIhF0MYRQzFKoIEw5KgibC+P3BwSCYIkRxFGEjiGCCjgSDBEHMU4AmIhR1OgLGUgIQQSMCqyE1I7B5OIS3hiMeKwNsvQiIAgg4HwDPopYgQxO5hEiEok7XyEW+bL2C4bpqRIwhKInRBIDgT35Ab5GDFh3SSYyRSzebNhmnSatbdNOVthANIQhNahbkfgOze5UYU6IPjFlqoPiHcfwk2kjD+L2HPfBj9C6Dk83K2DT7LDqm8LPnvz1oeLBV/D3ddwF8xkjYLUQtcrY08qV6eugtyHD4kHxENKCH1YRPxsK0DyeUThz6sClDs0fq0Av4bETxASn2w8OzhyNda5KSYXFmWEblRuee8UXZZFg1qAuW+bVGp2ZdL6QjcNjKrRL+pGnatGL74D6dWynWxaFvWPVdmclfl8WtQIpWWOV2suc9K5p6tVwwPrdPBuh+h0yM59tFNvCT1oXmvQX1Z1K66y7IWVWPswWPKHIl+eVlpdz0qzuY3hwL2NGOp5mpsMSuqfgMgOKrALal9OuLNz+3KCxaxdSFllF8sa2I0Wf9dVCabFsp90/0U9tAxdSWzf1NSpsr7Ik025GCiyDH0Cg6DToG9WQOxgjd+wvX9Rn5b5mkdul2dq1swr9/YI/Liyax8Vk1w7Jri29Eqn1+NycRGOsn6uV8sZPIUFjCfOugiiAxWQLSfhOvZXJ2NXtpLCTgY7CdxyymSrfpJQJ+GuY391UkBSv7SwU9LukuBWjaldTMO94B1tvLIUt8l9XpjmvH1oTHodthoGfD+fjvWaKFbgufGvpfz7tk015FA1ZEtNGLdTz3CwRbjhta4KnQd+A+Tzcl57d+1QP9OpmcLjhh8ri+pfYVG+NdOTSgd5lbsXeN6urhd3qXun2U31XVVOXxQ3r4AyWwsYDtpVDuu0MjPLTLBLMZmrCexN1wApZI9rvaZiZmoFySfrzmLdEzBIbZIB8zTWeGdzlVUmh0ijIMuAG8+bq7JanXPRhTLZ//5ToEyjM11UJTpV4zFoBQ0wBpCwPpzrKdRyqHEMdk6wgu20t4q/5fgXCJCr/Or7O0aG/i06u0LNERqpfHalbPkYLJarpa42bOgmfFlm25YF4NyGIVzMPFlmWnue+QXDzQymcx67Ee4AqhotoEQk/QTy+dKyyBahbzq0dbu1juy1im7rGmYauOcNdY/JRl+CyVjfHpLBZLRvi68PYLK0nE6Bo6hwNdSPzmTrvK0gA17oiZX9eXSETv8RDDRv2t6z18pPGSa6BwUr/iAc2nhNaPQokLAASCJYzMNvGqjMokREkYwiSnnEJNmLktyNEtmP0l9KOOHpLZisZZGCKiXBf/zvv+GWWs7fgesPalbWfzoQtNWgTw3dhitgtmFp5gAAD4nWoMDv/ZGF7QaA7wfgzFRprkdVuoXByCPgoaBb1t7AQcHYvQhAVjHpTFVrFFRQ98AQ9v4BbL6w2ata+laneavWaaDYvi50Xdv4EzZCsb/7s8kyXQRuQy1oJrq4gT1AsYvQAofvCJfYrwy9aVsWYNBj17QkoekN6QAKrlyZBRq18qNWagQAkKgvMSNJHAlOGaeWJCMWVIy4owsE1JEIHh3W9mvh91P7UshMZ7lJTbNCMbeR4UXRQGGkXd6/W9tcaz2ztecPxatKFbX9enPTbocF4cCXDQ49f/1PaP7XIZ7cDvnUfvyBQnBESIIZFpFggC6LQgSAAEDB+SWPBImojD5GCFbLLYRa07oI8JMj9s+nRyg0302cej9uFSho8dCP0+83oBDRhs2lgwL8Noo2IIodFse8T7DkIIxpHOP2BPqwQPL4nFXfddWDnPTLqFRxAmtJIkkZwVHCfHoWfYy5kJxwkYhEko9RxL402WwHKqfeNTtRcyuaHlQTPX9c1ZBNXmBRImgcSQkeGE4JnCcEMh/4XiRiyfhHKIZemqoqq92V0PMdpc/IF0WHGLsd8ogMjvtyI7JxEiy+GQj3556HGfxu7mnt0809u49r49f03fOOFX7kmce/OnCGx7zNLTzGNGFEJkxICDdfVnIJCG6e6g46zT2y9IL7D0kwuM8ElwKKe/A3bNNJOH8nCRcipgA9TSLKPspLknw5KYvdEe80nPzgwkLe34AqnavMS4Yz4thLpnCB80h2H5JedYuVm+2t7OatNXeT+8EUCO+67XVFAnIICd7+zq72L5vWh95PTdYHhSAwBxHd70Ok3BOE7oHpd49B+xEZP35Eju2fh21FAYcPTbohQ7b5gtojSAQjoEyFXvHFYPVeL4x+J6zgoGD/zlvAaYHRJI59HIdmDucESN8xJgwnLPGuFfUTjrFMKKcR5xGPvxisssePFe3LeOvw5g/5McCWYDhjyDihuH3hQvuRPeBTKcAPY/pZ+dWg+62e+149/O+BZ/8HUEsHCH5TiVE2CQAA2jAAAFBLAQIUABQACAAIAO8j4UDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA7yPhQH5TiVE2CQAA2jAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADNCQAAAAA=" language=es /> </center>
| |
| | | | |
| − | ===Variante de Construcción Dinámica=== | + | {{Note|1=Se recomiendan los tutoriales [[Tutorial:Preparaciones Espiraladas|Preparaciones Espiraladas]] y [[Tutorial:Resolver Problemas Ilustrándolos|Resolver Problemas Ilustrándolos]] <small>(diseños de Centro Babbage</small>) }} |
| − | <center> | |
| − | <ggb_applet width="530" height="373" version="4.4" ggbBase64="UEsDBBQACAgIAE6nsUQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICABOp7FEAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1bbXPbNhL+3P4KjD6ld5ZEEOCLMnI6sjPtZcZtMnWuc3OZTAYkIQk1RbIkZUu53K+6n3B/7BYASZEiJVuyE8fXKrZBkIuX3Wf3wQJixt+vFiG65mkm4ui0hwdGD/HIjwMRzU57y3zad3vfv/h2POPxjHspQ9M4XbD8tEcHtLdpB7UBsWRjEZz2LOxjYnnTPguo16eYO32PUda3KbGDKbVMgv0eQqtMPI/in9mCZwnz+aU/5wt2EfssV33O8zx5Phze3NwMytEHcTobzmbeYJUFPQQzj7LTXnHxHLprNLohStw0DDz8x08Xuvu+iLKcRT7vIanVUrz49pvxjYiC+AbdiCCfgy6G3UNzLmZzqaY76qGhFEpA14T7ubjmGTStVZXO+SLpKTEWyeff6CsUVur0UCCuRcDT054xoCPTxoZLHEpcahLb6qE4FTzKC2FcDDosuxtfC36j+5VXakhqjBzAQGTCC/lpb8rCDNQS0TQFk8KM0iVUs3wdco+lZX0zIXwC/0BAfOSyL8BO20FWTrBtnTiGcWJZhp5KfdweyuM4VJ0a6NMnZBqmgU5kgXVhQmHb+pGh7xlEF6YuqC4sLUN1c6pFqZahWoaSPToW9Y2SxY2GlqWOpK4jBuXkrw2/SvktJd2aklgq8QlhOXtVECTnjdX8ZUGLqq2rjiqwoQtcPHTln5GsgGlsV13cUzVylGr4oGHbbmOWo+L6qH16Aj+u4Z5YDm2PWRtS93jAiJWWI/fuWpr3sm1lWbPLsqbVPSYxd6t5azhWVrVaVsUGMU8carYGtOkBBNB2oM4hQTf1o35bIzpGZ/TrEhflPtsfZ4eOSY2HJSeOiwmhbC5lC8PnfJHJKZIRslTYYWRBHNsO0IqF8AgKR8azibCFqAVV7CJblg4iMoQpIshFUg4TpNjIcuEPdVRnNrKgM3nX0YGOCEUWQViRGEVgB6SIEKxiEpCwLGRBIzk8NmUXxEbUhhpxEYU5Sg50JM8QaAh1GN5EBCMiG2MHmcAasj9MSwJBJnRpIttAtrI80ChQqKZPkHcRkdpAtCdxJirrznmYlEZSdhRRsswL2xVo+YugFMnjpnQQ+1dnla0Lec6yvKqAGCxcm/WxY7W8EKFgETtgxXTJUWvkfXin4gDbPoB3HnF1vE3BPQSAR1+cWXEXm+9i1r1r1mchOvJFSOzLc/mRtKkYE7izQZnYPZQtgStt62nTpbQWYiueVSjMUonfhv2alKqbbjNqXfrBKPUAPjUxNo9j1KeaPdr4abD4ERuBe9P40UsjtjtGvFN6/Cel/kmpXxelftOoKzhD5vFQRLNL6SUIXbNQxo0aYRpHOSodhOp7s5Qlc+FnlzzPoVWGfmPX7ILlfPUDSFfaKVk/jrI3aZyfx+FyEWUI+XFoVKrFIa5dm7VrUrumm4Q9Dq16xa5XnM6BY3iClhmHCcRpVvbKguCVlNiQAFjwdRSuz1LOrpJYKD2UrLKgOkIb86UfigBS+l8hEBSiYBdUnqipfXt5okaoW84jToPLdQbRgVb/5GkMdnTowKh/gGfW+hHBTvMROFXmMxnYdDQY1T8uPFoXzyxju0M1Nr+uIOpwO20Jef0qO4vDjSMq9c9Zki9TdT4KvpxKrSbRLOTKR9Q9f879Ky9eXWrnILqvt+sEaoaegDdTZkfAO6YF6/CsKD1dKhk5s0rKUDKGkjBKbxNB9RyPTCWhSk+XSgrcV0+t0BSXWmKjHEZkii2NXjNclPPLtGEZifyirOTCvypULRr8vFx4PN0YUUq8FPqYVR8pN8fBh46DDxhnPNzyxfEVTyMeFp4PmC/jZaYjuRYUEAdvWD6fRMEvfAY89YbJRSKH4bRo6fDALNwXC2jYIAMmHeDvMH19N+CzlBfyLFRH1xoC9dSo+3/rturqhzRevIqu34J3bU11PCz1GWd+KhLpxGDBaLZkM7ACzwB9WMKu+MZrA5ExWAGDei8yxEEnX3IyGDKXZj6fi9+XwpcJYZx9AKOzZT6P02q3ji6ZCP77nwgFHJ3zKI3RGfM8GBaGAI4D0CQThHwBHaBcebsKmArhyQe941d0H3u/AdFW67yWqCECz7ecXyWMyv0RC5M5k2lsYbSQrXnaMKPq8Kc42DYuYKd0BtpJZAfStxLOtVvqScNFAh2qCK9NiC1X0g7petsjvIoZt58oiDO0gvyWyC9H1sU3LB9rYaEaSqbQja363Y1zkMK3tXVvsfPZH9fO9IHN7MeLBYsCFKmU8QK4tLdJRpihfRoxrI2uDbrMy4epvjceFt20cJPkXIGSPj5s9zG9UZjeKUzfd6rhqyUoh+zoCvaWmdp+FG5g6Ku/iSDgKkHUS/TvkW6T6UVALJIQyCnfj9AbFQhNiNIOZCb7cdnireNgwRZRwFj4ocPp7sF0J24yBnbj49wnhMz9TBUtFzwVfmW78MO/WBB/wP9WNoYelmU/5bC77b5Rpm522E4X8WC27I732v31dJrxXJnEVSbo425Yim6yUJ6moIWI1CgLtpJWQczLIKfP+aUPSUC0+UJbz73IiUcqXFbSS0rOstStqVjV1m5Yf8VHSFua2HUGVBlH0gKdEXUnUjYO86PdkfiWr/Kp4GGwFY0bwLdj8iKOZiJdBvtDM6/6Ld2ganeMtxzLnRtfMYlCT34Fe78Q3mH6I0gZ/AMSwB95jPgqaZk85NEsnzeC2Ic9jZybugd5bMACnsk8T9k2XwZwHaIL1cstsKcsykJIB7fXSb1K/gq4xOm7Z9WU0F+QzJuL+0DV77973/KMs0PY+uyx2founIsHpPl5UMptQvILW2+BUYH0bnKCdkHyOoXsfxZHLGyA874B5E7BNojstmQohXmWILGnnQv1ccHpRpkMtdfY3Uzu3CM1UiYPJYm8iuT2lastXnvDe8V5Ik8kXkfKGeRrXXdl9q4ci3XkWOe3Ad6M2/PHh/zoNOt+ztKdf9GB/Cbkwfcw5yL1Qz5J/W6CnqC/omflqYqkB4DlfQdJg7RZQdyAne8H3Y8j4Scs3QDPHxv2oxbYdthapZOQHWErZjy6VjbMEFoZBd+vjZImyjsrrJxCPsPlooBrfgBOmooVmpTyk1JqYkrqMQcWJdiqPpDLTkgxxoTKi5a7TayCs75WfuEtN3t5GLu8/KOyC8zTsfDIcUeY2BYdjahb0IttW7ZL7JFrYey6+DNwTTvzABgkwexL/1r5xd6swjskq/COdYJqTymTxK/gjKVMFPttFO+SVlhPJa3wutKKg5KKx94MfN6jGzLATnsb8SChfcumogutSz6Tsu8gyE/QZo9xvtljPOtXkf9dM/Q9vbloB/jLg1j+/xtu/Ihwh2vY4nXnjGdFMggFKQBrQOgvizNypgU9LehDAenILec9STFyCaHsbCfF0dpZSgfDHb34F9+pynLjGdbDHAvsPivNdDxtNsWPncE0l67GOwXbK5RZrlDVOe4xgH3xJWk/AN4TAKBP2nSgMgaXNN6SGCl4yMCgjuW4pk1t17SMvecSTwss/wmAVUZLvwyX0YAQyNMdMnIMkzh26yWOJwvHbcfzXwMc3aHT3xE7dGC6RO2rTEJx9drOk8BqWH8BRL3HVfwXyxf/A1BLBwgD6APqhgoAABI6AABQSwECFAAUAAgICABOp7FERczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAE6nsUQD6APqhgoAABI6AAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAHgsAAAAA" language=es /></center>
| |
| | | | |
| − | {{Tutorial
| |
| − | |title=De diagonales en el cuadrado a la Calculadora de Probabilidades <small>Diseño de un Taller de LMS</small>
| |
| − | }}
| |
| | =Hacia un Tutorial= | | =Hacia un Tutorial= |
| | ==Cuadradeando== | | ==Cuadradeando== |
Tutorial: ¿Cómo sumar Comandos a la Construcción? ¿Cómo calcular Probabilidades?
¡Tantas formas de Trazar un Cuadrado!
Acaso un inicio "cuadrado" permita considerar modalidades y variantes de trazado hacia el dominio de comandos y herramientas. su empleo:
Estrellas Fraccionadas a Polígonos y...¿Cuadrados?
En el desarrollo de un escenario "estelar" se construyen alternativas de exploración, a partir de una circunferencia en que se gira una fracción de vuelta un segmento de radio para unir los vértices.
Nota: Son ilustrativos también los diversos tutoriales en "barra" a rediseñar y explorar.
El desafío plantea, tras una serie de exploraciones más o menos libres que lleven a encontrar las relaciones causales entre los valores de los deslizadores y el resultado gráfico, sería:
- establecer los distintos valores de la fracción expuesta que permita obtener el dibujo representativo del cuadrado. Sea...
- directamente dado que lo que se evidencia es el dibujo de una figura de cuatro lados, por lo pronto
- indirectamente dado que lo que se evidencia es un dibujo tal que uniendo algunos de los puntos que quedan expuestos con la Herramienta de Polígono lleva a la representación de un cuadrado
Finalmente, es posible ampliar la experimentación al circunscribir e inscribir figuras de análisis.
Hacia un Tutorial
Cuadradeando
Planteo
Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del  Polígono regular?
Polígono regular?
En este tutorial, se compara el cuadrado que puede crearse con la  Polígono regular con el de una
Polígono regular con el de una  herramienta personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
herramienta personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
1 Seleccionar una adecuada del Menú Apariencias y activar la Barra de Estilo en la Vista Gráfica para completar los preparativos.
Preparativos
Ocultar los ejes coordenados, exponer la cuadrícula y optar por la alternativa con la que se Ajusta a Cuadrícula' en la Barra de Estilo.
Paso a Paso
2 Marcar dos  puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
3 Trazar...
- el
 punto medio y la
punto medio y la  mediatriz entre estos puntos
mediatriz entre estos puntos
- la
 circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
- los
 puntos de intersección entre la mediatriz y la circunferencia
puntos de intersección entre la mediatriz y la circunferencia
- la
 semicricunferencia que se extiende entre uno y otro punto de intersección
semicricunferencia que se extiende entre uno y otro punto de intersección
- un
 punto sobre esta semicircunferencia
punto sobre esta semicircunferencia
- el punto que
 refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia
refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia
- las
 rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente.
rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente.
4 Construir el polígono que tiene como vértices:
- el punto sobre la semicircunferencia,
- uno de los extremos de la diagonal del cuadrado en marcha,
- el punto reflejado,
- el otro extremo de la diagonal
5 Desplazar el punto que se trazó sobre la semicircunferencia hasta que ocupe la posición en que parece un cuadrado.
Justificaciones y Controles
El boceto se traza de modo tal que el punto que se desplaza sobre la semicircunferencia, su reflejado y los contiguos - vértices de la diagonal - conformen...
- un rectángulo
- que deviene cuadrado cuando se lo lleva hasta uno de los de intersección - ambos son extremos del recorrido por el que hasta se lo podría animar.
Conviene controlar...
- de modo más certero este comportamiento, empleando las herramientas adecuadas para contar con información sobre valores y relaciones
- las argumentaciones respecto a las vinculaciones entre el resultado de los ensayos y lo que la construcción desencadena en todos los casos.
Un Quehacer a Proyectar y Compartir
Pese a que lo más evidente - desde la óptica docente - es que la primera de las actividades depende directamente del empleo de herramientas con las que es preciso familiarizarse, ambas se entrecruzan con operaciones sobre la construcción dinámica:
- en exploraciones - guiadas por un propósito - que van dando entidad a...
- justificaciones causales de los efectos de ciertas maniobras - ¿es rectángulo? - ¿siempre? - ¿cómo hacemos para asegurarlo? - ¿cuándo parece pasar a cuadrado? - ....
- las relaciones entre los elementos que es preciso develar para respaldar la cadena de causalidades
- las correlaciones entre efectos, trazado y propiedades en juego que requieren un estudio conceptual
- ... de hecho, es la necesidad de validar estas presunciones lo que da razón de ser a su estudio.
Este recorrido expone un modelo de quehacer matemático que, escasamente transitado en términos generales frente a los estudiantes y con ellos, permite proyectarlo como medio de formación que puede completarse en intercambios virtuales.
Herramientas para el Control de Ensayos y Presunciones
6 Emplear las herramientas necesarias para controlar qué tipo de cuadrilátero se ha construido. Por ejemplo:
- la que traza y mide sus
 ángulos para corroborar que, tal como parece, son rectos
ángulos para corroborar que, tal como parece, son rectos
- la que
 mide la longitud de cada lado
mide la longitud de cada lado
- la que informa sobre la
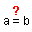 relación entre los segmentos de los lados y de las correspondientes rectas.
relación entre los segmentos de los lados y de las correspondientes rectas.
7 Procurar descripciones argumentadas sobre el tipo de cuadrilátero que se establece a medida que se desplaza el punto sobre la semicircunferencia.
Herramientas Propias para Completar las Disponibles
8 - Opción más Avanzada Dirigirse al manual para conocer la serie de pasos a partir de los cuáles, seleccionando el cuadrilátero creado como objeto de salida en la Nueva herramienta de la opción Creación de Herramienta Nueva del Menú de Herramientas, se puede crear la propia.
- En este caso, la que traza rectángulos (que pueden establecerse como cuadrados), dada su diagonal, como ilustra la siguiente figura.
- Habría que incluirlos en el listado correspondiente, si además del cuadrilátero (polígono), se deseara que otros elementos se expusieran en la salida (como los puntos vértices adicionales a los dados, los segmentos de lado, las rectas que los contienen, la semicircunferencia por la que se desplaza uno de los puntos de entrada, etc.).
- Una vez creada la herramienta, es posible cambiar el ícono que la acompaña así como otros detalles - nombre, ayuda -.
Tutorial: Diagonal de un Cuadrado
Basado en Diseño de un Taller de Centro Babbage
|
Calculadora de Probabilidades: Pestaña Distribución
|
Calculadora de Probabilidades
Calculadora
Con la  Calculadora de Probabilidades, una de las vistas principales de GeoGebra, se calculan y grafican distribuciones de probabilidad y realizan pruebas estadísticas.
Calculadora de Probabilidades, una de las vistas principales de GeoGebra, se calculan y grafican distribuciones de probabilidad y realizan pruebas estadísticas.
 (código 66)
(código 66)
Esta herramienta solo es accesible cuando:
A este instrumento  (código 66) se accede desde la caja de Herramientas que, por omisión, la encabeza:
(código 66) se accede desde la caja de Herramientas que, por omisión, la encabeza:
El Cálculo de Probabilidades es una de las perspectivas principales de GeoGebra , asociada a una herramienta que puede emplearse para calcular y graficar distribuciones de probabilidades así como realizar pruebas estadísticas.
|
Cálculo de probabilidades:
Pestaña Distribución
|
Pestaña:
Estadísticas
|
Distribuciones
La correspondiente pestaña de la herramienta despliega una lista de selección de diversas distribuciones de probabilidad a calcular y graficar:(Pascal, Binomial, ChiCuadrada ...).
Se pueden emplear los botones para establecer condiciones adicionales del gráfico. Botones como los siguientes:
 alterna entre la posibilidad acumulativa o no de la función de distribución
alterna entre la posibilidad acumulativa o no de la función de distribución

 modifican el gráfico para calcular una probabilidad acumulada. Por ejemplo:
modifican el gráfico para calcular una probabilidad acumulada. Por ejemplo:
. P(x ≤ X), P(x ≥ X)).
Basta seleccionar el tipo de intervalo usando los botones ofrecidos.
Luego, se debe ajustar el intervalo en las casillas de entrada de texto adyacentes o deslizar los marcadores correspondientes a lo largo del eje x en el mismo gráfico.
Estadísticas
La pestaña Estadísticas habilita a una variedad de pruebas y test.
Basta con indicar con cuál de la lista que despliega los disponibles.
Una vez realizada la selección, se deben ajustar los parámetros correspondientes.
GeoGebra automáticamente presentará los resultados del test estadístico.
Barra de Estilo Probable y Estadística
La Barra de Estilo presenta opciones para cambiar las características del gráfico, su configuración y hasta la posibilidad de  superponer la Curva Normal a la distribución que se va a
superponer la Curva Normal a la distribución que se va a  exportar.
exportar.
Distribuciones de Probabilidad
Entre las diversas distribuciones de probabilidad se cuenta la de Pascal, Binomial, ChiCuadrada y otras que, además, cuentan con el comando correspondiente.
Así, para...
- cambiar la distribución, basta un clic para escogerla, de entre las desplegadas y pasar a las casillas adyacentes para fijar sus parámetros
- calcular la probabilidad, basta un clic para indicar, entre los desplegados, el tipo de intervalo y ajustarlo en las casillas de texto
 Atención: También puede desplazarse directamente los puntos del eje x del gráfico para determinar el intervalo.
Atención: También puede desplazarse directamente los puntos del eje x del gráfico para determinar el intervalo. Nota: Como se aprecia en las casillas disponibles para los ajustes, se puede indicar que se quiere...
- calcular la probabilidad de obtener un valor...
- contenido dentro de cierto intervalo
- menor o mayor que el que se fijara como término de comparación
- indicar el Intervalo del rango de análisis, recurriendo a los iconos de Lado Izquierdo o Lado Derecho, bajo la representación gráfica del encuadre de esta herramienta.
La flechita  Barra de Estilo (In)Activa en extremo izquierdo de la caja de esta herramienta, abre y cierra esta Barra.
Barra de Estilo (In)Activa en extremo izquierdo de la caja de esta herramienta, abre y cierra esta Barra.
Activada, desde sus iconos se puede configurar el gráfico seleccionado e Indicar la modalidad en que se lo Exporta.
El último, está siempre disponible y los restantes dependerán del tipo de gráfico estadístico seleccionado. Los ilustrados se vinculan al Binomial:
Nota: A la izquierda del visor que indica el tipo de gráfico elegido de la lista desplegable, aparece el botón del ícono que establece si se va a optar o no por el Acumulado, tal como lo ilustra la figura.
Opciones de Estilo y de Probabilidad en Barra
La Barra de Estilo presenta opciones para cambiar las características del gráfico, su configuración y la modalidad en que se lo Exporta.
Nota: Además de las posibilidades que se sintetizan en la imagen, como el estilo de representación y la modalidad para exportar esos gráficos, pueden modificarse también, desde la Barra de Estilo, alternativas a las que puede accederse desde la pestaña Estadística.
Alternativas Estadísticas
Algunas de las opciones disponibles pueden apreciarse en la imagen ilustrativa.
Arrastrar y Desplazar
Cuando el ratón o mouse se ubica en la zona superior de la zona del gráfico, el cursor aparece como manito para arrastrar el boceto a la Vista Gráfica 1 o a la 2 y/o crear un nuevo gráfico.
Con las maniobras adecuadas, incluso se puede arrastrar el gráfico a cualquier aplicación que admita imágenes. Sea el documento de un procesador de textos en que se inserte o una producción diferente de otro utilitario que la acepte como tal.
 Atención: Para exportar se ofrecen alternativas en la Barra de Estilo de esta herramienta.
Atención: Para exportar se ofrecen alternativas en la Barra de Estilo de esta herramienta.
La Copia puede facilitar algunas de estas maniobras.
Lo que se Exporta como Imagen Gráfica puede adoptar diversos formatos a escoger de la correspondiente lista desplegable.Alternativas Gráficas y sus Intervalos
Según el tipo de gráfico, aparecen diversos recursos para configurarlo y, para cada uno de ellos, los intervalos o rango de valores a exponer, como sintetiza la figura
Ejemplos:
X sigue una distribución normal de media 2 y desviación estándar 0.7
Los gráficos pueden emplearse para...
- Representar la función de densidad.
- Calcular la probabilidad del suceso "1 ≤ X ≤ 3".
Basta con elegir Normal en la lista desplegable, anotando en los correspondientes campos, 2 en μ y 0.7 para σ
Un clic en  para completar con
para completar con 1 y 3los campos de la cota inferior y de la superior, respectivamente.
La respuesta a la segunda parte de esta pregunta es P ("1 ≤ X ≤ 3") = 0.85redondeo a 2 decimales
- Determinar el intervalo centrado en 2 en que X cuenta con probabilidad 0.95.
Se empieza por...
- clic en
 anotando '='
anotando '=' 0.025 ( \frac{1 - 0.95}{2} )
- clic en
 anotando '='
anotando '=' 0.025,
- clic en
 anotando '='
anotando '=' 0.975
... y se puede encontrar la otra por simetría con respecto a 2.
 ->
->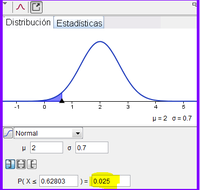
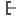 ->
->
 ->
->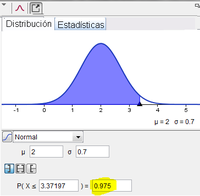
- La respuesta a esta pregunta es el intervalo [0.628, 3.372]redondeo a 3 decimales
Finalmente, para verificar...
- clic en
 anotando como límite inferior
anotando como límite inferior 0.628 y superior 3.372
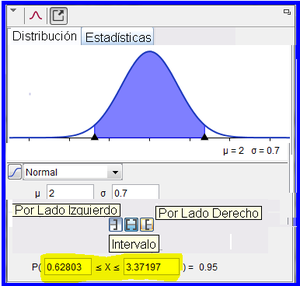
Barra de estilo de la Calculadora de Probabilidades
La Barra de estilo de la Calculadora de Probabilidades provee opciones para  superponer tu distribución con la Curva Normal y para
superponer tu distribución con la Curva Normal y para  exportar el gráfico.
exportar el gráfico.
Nota: Se puede exportar la distribución como una imagen (.png), copiarla al portapapeles (solo para GeoGebra Escritorio) o copiarla en la  Vista Gráfica.
Vista Gráfica.
Arrastrar y soltar: En la versión de GeoGebra Escritorio, se puede Arrastrar y soltar para transferir el gráfico de la distribución tanto a la  Vista Gráfica como a otra aplicación que acepte imágenes.
Basta ubicar el cursor en la parte superior de la pantalla de la
Vista Gráfica como a otra aplicación que acepte imágenes.
Basta ubicar el cursor en la parte superior de la pantalla de la  Calculadora de Probabilidades y, cuando pase a aparecer como una man, arrastrar el gráfico a la
Calculadora de Probabilidades y, cuando pase a aparecer como una man, arrastrar el gráfico a la  Vista Gráfica 1 o 2. Se crea así un nuevo gráfico o se arrastra su imagen a otra aplicación.
Vista Gráfica 1 o 2. Se crea así un nuevo gráfico o se arrastra su imagen a otra aplicación.
Estadísticas en breve
La pestaña Estadística permite realizar una variedad de pruebas estadísticas.
Basta seleccionar la prueba a realizar del menú desplegable (por ejemplo, Test Z de una media) y especificar tu Hipótesis Nula, así como tu Hipótesis Alternativa. A continuación, se pueden ajustar los parámetros de la prueba desde las cajas de texto para que GeoGebra proporcione los resultados automáticamente.

![]() Polígono regular?
Polígono regular?
![]() Polígono regular con el de una
Polígono regular con el de una ![]() herramienta personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
herramienta personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
![]() puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
 punto medio y la
punto medio y la  mediatriz entre estos puntos
mediatriz entre estos puntos circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos. puntos de intersección entre la mediatriz y la circunferencia
puntos de intersección entre la mediatriz y la circunferencia semicricunferencia que se extiende entre uno y otro punto de intersección
semicricunferencia que se extiende entre uno y otro punto de intersección punto sobre esta semicircunferencia
punto sobre esta semicircunferencia refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia
refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente.
rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente. ángulos para corroborar que, tal como parece, son rectos
ángulos para corroborar que, tal como parece, son rectos mide la longitud de cada lado
mide la longitud de cada lado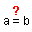 relación entre los segmentos de los lados y de las correspondientes rectas.
relación entre los segmentos de los lados y de las correspondientes rectas.
![]() Calculadora de Probabilidades, una de las vistas principales de GeoGebra, se calculan y grafican distribuciones de probabilidad y realizan pruebas estadísticas.
Calculadora de Probabilidades, una de las vistas principales de GeoGebra, se calculan y grafican distribuciones de probabilidad y realizan pruebas estadísticas.
 Hoja de Cálculo o la vista
Hoja de Cálculo o la vista  CAS. o
CAS. o![]() (código 66) se accede desde la caja de Herramientas que, por omisión, la encabeza:
(código 66) se accede desde la caja de Herramientas que, por omisión, la encabeza:
 de la
de la  Hoja de Cálculo
Hoja de Cálculo de la
de la  Vista CAS
Vista CAS
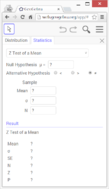
 alterna entre la posibilidad acumulativa o no de la función de distribución
alterna entre la posibilidad acumulativa o no de la función de distribución

 modifican el gráfico para calcular una probabilidad acumulada. Por ejemplo:
modifican el gráfico para calcular una probabilidad acumulada. Por ejemplo:![]() superponer la Curva Normal a la distribución que se va a
superponer la Curva Normal a la distribución que se va a ![]() exportar.
exportar.
 Barra de Estilo Calculada
Barra de Estilo Calculada![]() Barra de Estilo (In)Activa en extremo izquierdo de la caja de esta herramienta, abre y cierra esta Barra.
Barra de Estilo (In)Activa en extremo izquierdo de la caja de esta herramienta, abre y cierra esta Barra. Barra de Estilo para Optar
Barra de Estilo para Optar para completar con
para completar con 



![]() superponer tu distribución con la Curva Normal y para
superponer tu distribución con la Curva Normal y para ![]() exportar el gráfico.
exportar el gráfico.
![]() Vista Gráfica como a otra aplicación que acepte imágenes.
Basta ubicar el cursor en la parte superior de la pantalla de la
Vista Gráfica como a otra aplicación que acepte imágenes.
Basta ubicar el cursor en la parte superior de la pantalla de la ![]() Calculadora de Probabilidades y, cuando pase a aparecer como una man, arrastrar el gráfico a la
Calculadora de Probabilidades y, cuando pase a aparecer como una man, arrastrar el gráfico a la ![]() Vista Gráfica 1 o 2. Se crea así un nuevo gráfico o se arrastra su imagen a otra aplicación.
Vista Gráfica 1 o 2. Se crea así un nuevo gráfico o se arrastra su imagen a otra aplicación.