Tutorial:Cuadrilátero EquiDiagonal
Trazando Dinámicamente una Construcción Geométrica
Propuesta Inicial
La propuesta se abre en dos alternativas:
- Crear el escenario de trabajo desde el que se van plantear, a posteriori, desafíos diversos para destinatarios que no tengan, así, necesidad de llevar adelante todas las maniobras de partida
- Encarar los preparativos junto a los destinatarios y frente a ellos para que, mientras sigan la ilación de pasos vayan discerniendo cuáles son las relaciones entre los elementos en juego y los mecanismos operativos básicos de GeoGebra.
Sea cual fuera la modalidad adoptada, es aconsejable anticipar qué cuestión que provoca a este boceto, planteada según criterio de quien mediará la actividad que se espera desencadene. Por ejemplo:
- Dicen algunos por allí que para que un cuadrilátero resulte paralelogramo...
- deben ser iguales sus diagonales.
- Otros sostienen que esta...
- es condición necesaria pero no suficiente
- Los que no guardan desconcertado silencio exponen su desacuerdo. Rebaten señalando que...
- no se requiere tal igualdad. Igualdad que se registra en algunos paralelogramos (pero no en todos) así como en cuadriláteros que no son.
Idea: Para saldar con algunos datos este debate, se propone la siguiente figura de análisis que se invita a trazar y/o a explorar cuando esté lista.Apariencia Conveniente
1 Seleccionando del Menú Apariencias la que resulte conveniente para esta construcción geométrica, se encaran a continuación los preparativos.
Preparativos
2 Conviene dejar abierta exclusivamente la Vista Gráfica y...
- Activar la Barra de Estilo
- Ocultar los Ejes Coordenados
- Exponer la Cuadrícula
- Optar por la alternativa que Ajusta a Cuadrícula los puntos o elementos durante los desplazamientos, para facilitar la precisión de ciertos ensayos.
Dibujos de Figuras... con GeoGebra
Punto a Punto
3 Se pasan a emplear las diversas herramientas geométricas básicas para operar sobre la 
Vista Gráfica.
La siguiente tabla señala la secuencia del trazado:
| Nº | Nombre | Icono | Definición | Valor |
|---|---|---|---|---|
| 1 | Punto A |  |
A = (0, 3) | |
| 2 | Punto C | |
C = (3, 1) | |
| 3 | Punto M |  |
Punto Medio de A, C | M = (1.5, 2) |
| 4 | Segmento b |  |
Segmento [A, M] | b = 1.8 |
Puntales del Cuadrilátero en Marcha
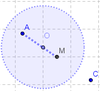
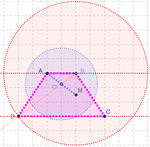
3 Se controla que todos los elementos básicos estén convenientemente vinculados. Hasta aquí, simplemente se crearon:
- los puntos libres A y C, vértices opuestos de una de las diagonales del futuro cuadrilátero
- el punto medio M entre A y C que permiten establecer la longitud del radio de la circunferencia cuyo diámetro - en torno al punto que será el de cruce las diagonales - fijará la distancia entre el otro par de vértices.
- el segmento entre A y M sobre el que se desplazará el punto O de cruce con la otra diagonal del cuadrilátero en marcha.
La ilustración expone este primer conjunto de elementos.
Avanzando en las Condiciones del Cuadrilátero
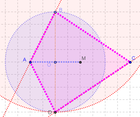
El área en que se van a ubicar uno de los dos vértices de la otra diagonal, de la misma longitud que la primera, se establece con el Compás con centro en O y radio igual a la longitud entre A y C, como se ilustra.
| Nº | Nombre | Icono | Definición | Valor |
|---|---|---|---|---|
| 5 | Punto O | |
Punto sobre b | O = (0.9, 2.4) |
| 6 | Circunferencia c |  |
Circunferencia con centro O y radio Segmento[A, M] | c: (x - 0.9)² + (y - 2.4)² = 3.25 |
| 7 | Punto B |  |
Punto en c | B = (1.83, 3.11) |
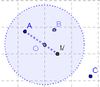
4 Se emplea la correspondiente herramienta para ubicar en ese círculo - dentro de c y hasta la circunferencia que lo rodea - al punto B, como se ilustra
B es uno de los extremos de la segunda diagonal en marcha.
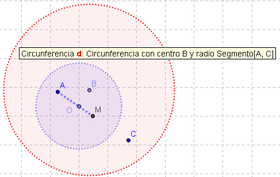
5 Para establecer la distancia a la que se encuentra, desde B el vértice opuesto de esa segunda diagonal en marcha, se traza con el compás, la circunferencia con un radio cuya longitud es igual a la de la primera diagonal - distancia de A a C - y tiene centro en B.
6 La 
semirrecta con origen en B, 
intereseca a la circunferencia recién trazada con el compás - con centro en B y radio de longitud y igual a la distancia entre A y C- , en el punto D.
Este punto de intersección, D, será el vértice opuesto a B en esta segunda diagonal.
Punteando el Cuadrilátero Equidiagonal
7 Las últimas maniobras de trazado se completan creando el polígono ABCD con la 
correspondiente herramienta, pulsando punto por punto - A, B, C, D y nuevamente A para cerrarlo.
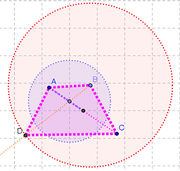
Cerrando el Cuadrilátero
En la tabla siguiente se ilustran los pasos finales de la construcción.
| Nº | Nombre | Icono | Definición | Valor |
|---|---|---|---|---|
| 8 | Circunferencia d | |
Circunferencia con centro B y radio Segmento[A, C] | d: (x - 1.83)² + (y - 3.11)² = 13 |
| 9 | Semirrecta e |  |
Semirrecta que pasa por B, O | e: 0.72x - 0.93y = -1.58 |
| 10 | Punto D | |
Punto de intersección de d, e | D = (-1.02, 0.91) |
| 11 | Cuadrilátero cua | |
Polígono A, B, C, D | cua = 6.16 |
Ajustes en pro de Datos Ilustrativos
Sin ser necesarias para llevar adelante la construcción, es conveniente:
- trazar también
sendas diagonales
uno de los ángulos entre las diagonales y los del cuadrilátero.
establecer las distancias entre los vértices del cuadrilátero, así como otros datos que permitan tener información sobre medidas.- cambiarle el nombre cuadrilátero por uno representativo y acaso más breve.
8 Desde la opción Renombra del Menú Contextual que se despliega con un clic derecho del ratón o mouse sobre el polígono, se le puede asignar un nombre más propicio que el de polígono1 que tiene de origen. Por ejemplo, cua.
Explorando el Cuadrilátero
9 Se pueden realizar ahora todas las maniobras necesarias para controlar que las diagonales del cuadrilátero sean iguales y hasta indagar qué condiciones de construcción así lo garantizan. Esto implica una justificación en términos matemáticos aunque no necesariamente rigurosa al punto de detener a los destinatarios en sus primeros intentos de argumentación.
Ensayos sobre el Cuadrilátero
La alternativa que se abre cuando se ha completado el trazado del polígono, es la que lleva a explorar qué condiciones deben procurarse para...
- lograr que se convierta en cuadriláteros de distinto tipo - desde trapecios a rombos, los que no resulten ni siquiera trapecios... etc. -
- controlar que lo que parece ser cierto tipo de cuadrilátero cumpla con las condiciones que así lo garantizan
Herramienta de Relación puede ser muy útil en esta última etapa. Ajuste a Cuadrícula Facilitando Ensayos
La construcción se ideó para facilitar ciertos ensayos. Como los que requieren que uno de los topes para ubicar...
- el punto de cruce de las diagonales sea el punto medio de la primera
- el extremo de la segunda diagonal tenga como límite la distancia equivalente a la mitad.
Para establecer otras relaciones específicas entre medidas conviene apelar a la cuadrícula como guía. Por ejemplo, para que las diagonales se crucen de modo consistente con las del...
- trapecio isósceles o
- romboide
... las maniobras se agilizan acudiendo a estas posiciones que se ajustan a la cuadrícula,
Medir para Controlar Relaciones
La Herramienta de Relación permite determinar, por ejemplo, igualdad de longitudes entre segmentos o de paralelismo entre rectas.
Atención: 
herramienta pertinente.
Con las Mediciones se puede controlar si son iguales...
- un par de ángulos o si alguno resulta recto.
- las longitudes de lados, diagonales y/o semidiagonales.
10 Una actividad pautada para guiar los ensayos puede llevar a una síntesis sobre una tabla que resuma las conclusiones a las que lleguen los participantes.
Reglas de Juego para Ensayar y Argumentar
Posiblemente, durante la mediación docente resulte necesario recordar que si bien un solo contraejemplo basta para descartar una teoría, multiplicidad de ejemplos no alcanzan para garantizarla (aunque la convicción ganada impulse a creerlo).
