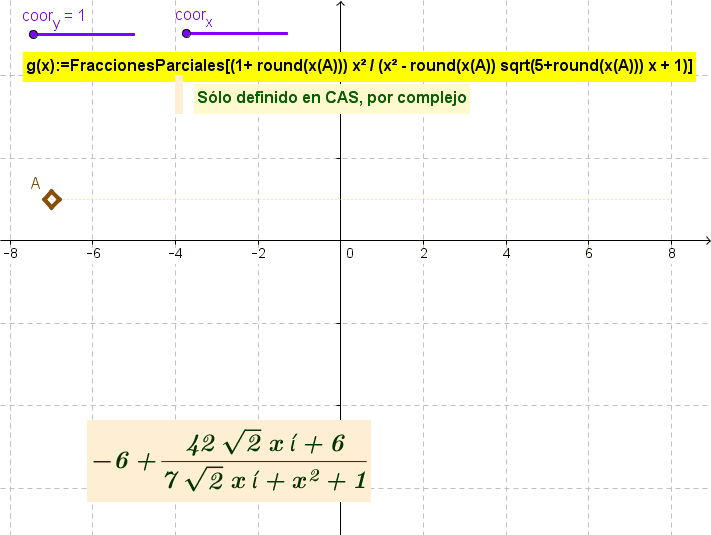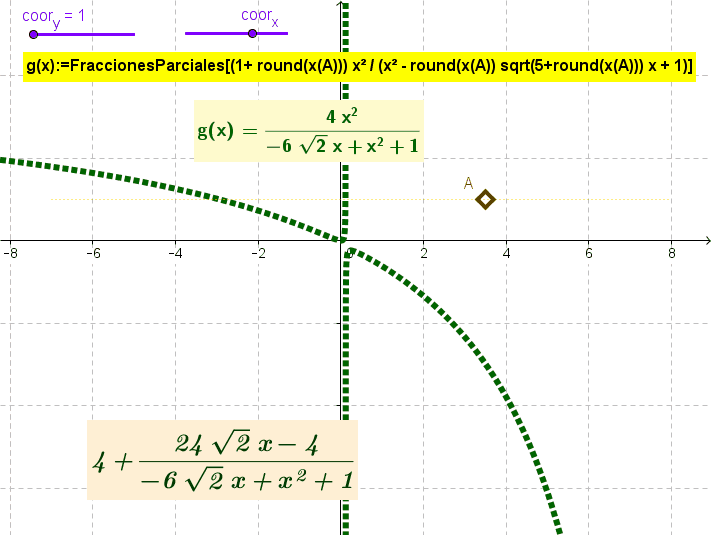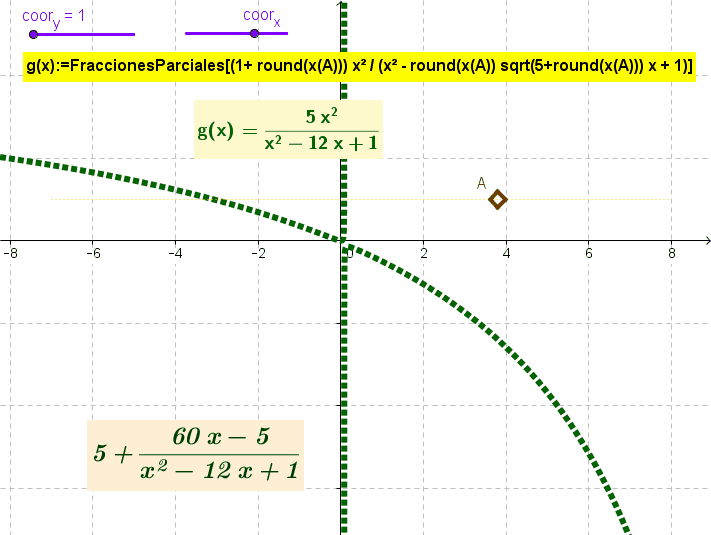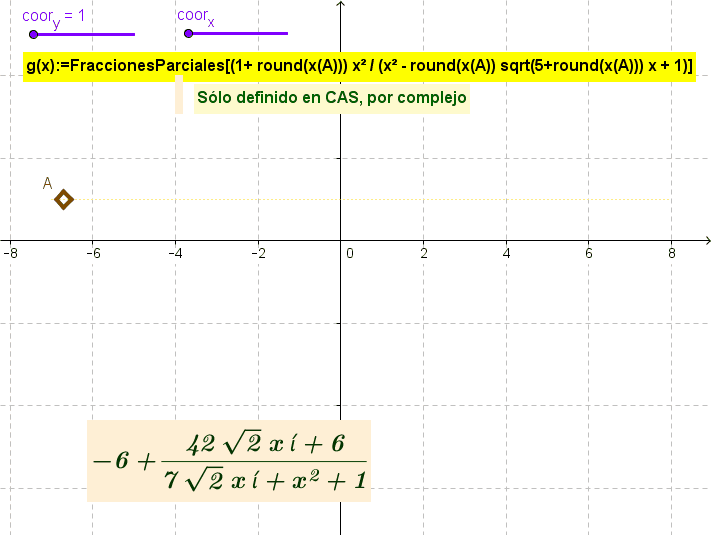
Comando FraccionesParciales

De GeoGebra Manual
| Página en proceso de traducción. |
FraccionesParciales
Categorías de Comandos (todos)
- FraccionesParciales( <Función> )
- Establece y grafica, de ser posible, el resultado de aplicarle a la función el caso de factoreo denominado de fracciones parciales (en inglés, partial fraction), respecto de la variable principal.
- Nota: En la Vista Gráfica activa se ilustra su representación.
- Ejemplos:
FraccionesParciales[x^2 / (x^2 - 2x + 1)]da por resultado 1 + \frac{2}{x - 1} + \frac{1}{(x -1)^2}FraccionesParciales[(3x - 2) (3x + 2) / (1 + x)]da 9 x - 9 + \frac{5}{x + 1}
- Nota: Desde la version 4.2, factoriza también denominadores y admite como variable, además de
x, tambiényy hastaz.
 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
Este comando admite literales en esta vista y suma a la previa, la siguiente sintaxis con exclusividad.
- FraccionesParciales( <Función>, <Variable> )
- Establece, de ser posible, la fracción parcial de la función en la variable especificada.
- Ejemplos:
FraccionesParciales[ñ^2 / (ñ^2 - 2ñ + 1), ñ]da 1 + \frac{2}{ñ - 1} + \frac{1}{(ñ-1)²}FraccionesParciales[k x^2 / (x^2 - 2 k x + ñ), x]da por resultado la siguente expresión k + \frac{2 k² x - k ñ }{x² + ñ - 2 k x }
- Nota:
Cuando la función incluye literales se establece la correspondiente fórmula. - FraccionesParciales( <Función> )
- Establece y grafica, de ser posible, el resultado de aplicarle a la función el caso de factoreo denominado de fracciones parciales (en inglés, partial fraction), respecto de la variable principal.
- Ejemplos:
FraccionesParciales[3 t^2 / (t^2 - 2 t + 1)]da, siendo en este casotla variable principal, 3 + \frac{6}{(t - 1)} + \frac{3}{(t - 1)²}FraccionesParciales[k x^2 / (x^2 - 2 k x + ñ)]da:-\frac{x}{2} + \frac{x^3 + x ñ}{2 (x^2 + ñ)- 4 k x}
- Nota: Cuando es viable, al tildar el redondelito que encabeza la fila correspondiente, la función resultante cobra entidad algebraica y gráfica como es la del siguiente caso.
- Ejemplo:
q(x):=FraccionesParciales[3x² / (x² - 2sqrt(7) x + 1)]establece y grafica la siguiente función q(x) = \frac{3 x²}{x² + 1 - 2 \sqrt{7} x } - Nota: Ver también el comando MCM