Diferencia entre revisiones de «Comando Factoriza»

De GeoGebra Manual
m (pendiente de traducción) |
|||
| Línea 1: | Línea 1: | ||
| − | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|cas=true|algebra|Factoriza}};Factoriza[ <Polinomio> ]:Crea y [[Vista Gráfica|grafica]] cuando es posible, la [[Funciones|función]] resultante de factorizar el ''[[:w:es:Polinomio#Operaciones_con_polinomios|polinomio]]'' de entrada. | + | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|cas=true|algebra|Factoriza}} |
| + | {{revisar}} | ||
| + | ;Factoriza[ <Polinomio> ]:Crea y [[Vista Gráfica|grafica]] cuando es posible, la [[Funciones|función]] resultante de factorizar el ''[[:w:es:Polinomio#Operaciones_con_polinomios|polinomio]]'' de entrada. | ||
:{{Examples|1=<br>'''<code><nowiki>Factoriza[x^2 + x - 6]</nowiki></code>''' crea y [[Vista Gráfica|grafica]] la [[Funciones|función]] ''(x - 2) (x + 3)''<br>'''<code><nowiki>Factoriza[x³+1.5 x²-1/3x-1/2]</nowiki></code>''' crea y [[Vista Gráfica|grafica]] la [[Funciones|función]] ''<math> (2 x + 3) \frac{ (3 x^2 - 1)}{6} </math>''<br><br>'''<code>Factoriza[x³ + 1 / 2 sqrt(3) x² - 1 / 3 sqrt(7) x - 1 / 6 sqrt(21)]</code>''' da <math>{\frac{1}{6} \left( -3 x^{2} + \sqrt{7} \right) \left( -2 x - \sqrt{3} \right)}</math> el resultado de factorizar <math>x³ + \frac{1}{2} \sqrt{3} x² - \frac{1}{3} \sqrt{7} x - \frac{1}{6} \sqrt{21}</math> | :{{Examples|1=<br>'''<code><nowiki>Factoriza[x^2 + x - 6]</nowiki></code>''' crea y [[Vista Gráfica|grafica]] la [[Funciones|función]] ''(x - 2) (x + 3)''<br>'''<code><nowiki>Factoriza[x³+1.5 x²-1/3x-1/2]</nowiki></code>''' crea y [[Vista Gráfica|grafica]] la [[Funciones|función]] ''<math> (2 x + 3) \frac{ (3 x^2 - 1)}{6} </math>''<br><br>'''<code>Factoriza[x³ + 1 / 2 sqrt(3) x² - 1 / 3 sqrt(7) x - 1 / 6 sqrt(21)]</code>''' da <math>{\frac{1}{6} \left( -3 x^{2} + \sqrt{7} \right) \left( -2 x - \sqrt{3} \right)}</math> el resultado de factorizar <math>x³ + \frac{1}{2} \sqrt{3} x² - \frac{1}{3} \sqrt{7} x - \frac{1}{6} \sqrt{21}</math> | ||
}} | }} | ||
Revisión del 20:18 31 jul 2017
Factoriza
Categorías de Comandos (todos)
| Página en proceso de traducción. |
- Factoriza[ <Polinomio> ]
- Crea y grafica cuando es posible, la función resultante de factorizar el polinomio de entrada.
- Ejemplos:
Factoriza[x^2 + x - 6]crea y grafica la función (x - 2) (x + 3)Factoriza[x³+1.5 x²-1/3x-1/2]crea y grafica la función (2 x + 3) \frac{ (3 x^2 - 1)}{6}Factoriza[x³ + 1 / 2 sqrt(3) x² - 1 / 3 sqrt(7) x - 1 / 6 sqrt(21)]da {\frac{1}{6} \left( -3 x^{2} + \sqrt{7} \right) \left( -2 x - \sqrt{3} \right)} el resultado de factorizar x³ + \frac{1}{2} \sqrt{3} x² - \frac{1}{3} \sqrt{7} x - \frac{1}{6} \sqrt{21}
- Nota: Las variables admitidas son
x,zey - Ejemplos:
Factoriza[x³-y³]resulta (x²+x y+y²) (x-y)Factoriza[y²- z²]crea la función multivariable (y + z) (y - z)
- Nota: Operando en línea, este comando requiere de la carga del Sistema CAS de Álgebra. Esta maniobra puede resultar lenta en ocasiones y/o en ciertos equipos.
 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
A la previa se suma exclusividades de esta vista: indicar la variable de factorización y/o incluir literales para operar simbólicamente.
- Factoriza[ <Expresión>, <Variable> ]
- Factoriza la expresión respecto de la variable dada
- Ejemplos:
Factoriza[v^(2 k/ñ) - y^(2 k/ñ), k]da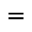 { \left( v^{\frac{k}{ñ} } + y^{\frac{k}{ñ} } \right) \left( v^{\frac{k}{ñ} } - y^{\frac{k}{ñ} } \right)}, factorización de:
{ \left( v^{\frac{k}{ñ} } + y^{\frac{k}{ñ} } \right) \left( v^{\frac{k}{ñ} } - y^{\frac{k}{ñ} } \right)}, factorización de:
v2 k/ñ - y2 k/ñ respecto de k.Factoriza[w^2 - y^2, y]da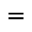 (-y - w) (y - w), factorización de w2 - y2 respecto de y
(-y - w) (y - w), factorización de w2 - y2 respecto de yFactoriza[w^2 - y^2, w]da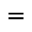 (y + w) (-y + w), factorización de w2 - y2 con respecto a w
(y + w) (-y + w), factorización de w2 - y2 con respecto a w
Factoriza[z³ + 1 / 2 sqrt(3) z² - 1 / 3 sqrt(7) z - 1 / 6 sqrt(21)]da como resultado aproximado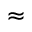 (z + 0.58) (z + 1.5) (z - 0.58) y es evaluado como
(z + 0.58) (z + 1.5) (z - 0.58) y es evaluado como 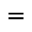 {\frac{1}{6} \left( -3 z^{2} + \sqrt{7} \right) \left( -2 z - \sqrt{3} \right)}
{\frac{1}{6} \left( -3 z^{2} + \sqrt{7} \right) \left( -2 z - \sqrt{3} \right)}
- Factoriza[ <Expresión> ]
- Crea. y grafica cuando es posible, la función resultante de factorizar la entrada. La expresión puede ser un polinomio y, en cualquier caso, incluir literales.
- Ejemplos:
Factoriza[ñ^2 + 2 ñ ü + ü^2]da por resultado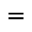 { \left( ñ + ü \right)^{2} }
{ \left( ñ + ü \right)^{2} } Factoriza[x^(3n/2) - y^(3n/2)]da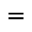 { \left( \sqrt{y^{n} } \sqrt{x^{n} } + x^{n} + y^{n} \right) \left( \sqrt{x^{n} } - \sqrt{y^{n} } \right)}
{ \left( \sqrt{y^{n} } \sqrt{x^{n} } + x^{n} + y^{n} \right) \left( \sqrt{x^{n} } - \sqrt{y^{n} } \right)}Factoriza[-6 k^3 x ñ^2 - 3k^2 x^2 ñ - 2k^2 ñ^3 + 3k x^3 - k x ñ^2 + x^2 ñ]da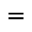 (3x k + ñ) (x + k ñ) (x-2k ñ)
(3x k + ñ) (x + k ñ) (x-2k ñ)Factoriza[y^(3k)+z^(3k)]da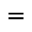 (y2k - zk yk + z2k) (yk + zk)
(y2k - zk yk + z2k) (yk + zk)
- Notas:
Este comando opera sobre el conjunto ℚ de los Números Racionales
Las versiones más recientes se extienden al conjunto ℝ de los reales
Para obrar con el conjunto ℂ de los complejos, ver el comando FactorC
Para factorizar sobre el conjunto ℂ de los complejos irracionales ver el comando FactorizaCI y para los irracionales, FactorizaI




