Ableitung (Befehl)

Aus GeoGebra Manual
- Ableitung( <Funktion> )
- Liefert die Ableitung der Funktion.
- Beispiel:
Ableitung[x^3 + x^2 + x]liefert 3x² + 2x + 1. - Ableitung( <Funktion>, <Grad der Ableitung> )
- Liefert die n-te Ableitung der Funktion, wobei n gleich <Grad der Ableitung> ist.
- Beispiel:
Ableitung[x^3 + x^2 + x, 2]liefert 6x + 2. - Ableitung( <Funktion>, <Variable> )
- Liefert die partielle Ableitung der Funktion nach der gegebenen Variable.
- Beispiel:
Ableitung[x^3 y^2 + y^2 + x y, y]liefert 2x³y + x + 2y. - Ableitung( <Funktion>, <Variable>, <Grad der Ableitung> )
- Liefert die n-te partielle Ableitung der Funktion nach der gegebenen Variable, wobei n gleich <Grad der Ableitung> ist.
- Beispiel:
Ableitung[x^3 + 3x y, x, 2]liefert 6x. - Ableitung( <Kurve> )
- Liefert die Ableitung der Kurve.
- Beispiel:
Ableitung[Kurve[cos(t), t sin(t), t, 0, π]]liefert die Kurve x = -sin(t), y = sin(t) + t cos(t). - Anmerkung: Die Kurve muss in parametrischer Form gegeben sein.
- Ableitung( <Kurve>, <Grad der Ableitung> )
- Liefert die n-te Ableitung der Kurve, wobei n gleich <Grad der Ableitung> ist.
- Beispiel:
Ableitung[Kurve[cos(t), t sin(t), t, 0, π], 2]liefert die Kurve x = -cos(t), y = 2cos(t) - t sin(t). - Anmerkung: Die Kurve muss in parametrischer Form gegeben sein.
Anmerkung: Sie können
f'(x) statt Ableitung[f] schreiben, oder f''(x) statt Ableitung[f, 2] und so weiter.CAS-Ansicht
- Ableitung( <Ausdruck> )
- Liefert die Ableitung der Funktion/des Ausdrucks nach der Hauptvariable.
- Beispiel:
Ableitung[x^2]liefert 2x. - Ableitung( <Ausdruck>, <Variable> )
- Liefert die Ableitung der Funktion/des Ausdrucks nach der gegebenen Variable.
- Beispiel:
Ableitung[a x^3, a]liefert x³. - Ableitung( <Ausdruck>, <Variable>, <Grad der Ableitung> )
- Liefert die n-te Ableitung der Funktion/des Ausdrucks nach einer Variable, wobei n gleich <Grad der Ableitung> ist.
- Beispiel:
Ableitung[y x^3, x, 2]liefert 6xy.Ableitung[x³ + 3x y, x, 2]liefert 6x.
Kommentare
Weitere Tipps[Bearbeiten]
- Den Ausdruck
f'(x)kann man auch verwenden um die Ableitung an einer bestimmten Stelle zu berechnen. So gibtf'(2)den Ableitungswert an der Stelle 2 als Zahl aus. - Hat man eine Kurve
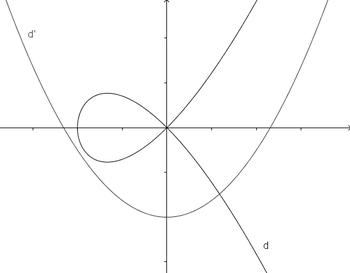
dmitKurve[t² - 1, t (t² - 1), t, -5, 5]erstellt und bestimmt dazu die AbleitungAbleitung[d]so erhält man die Ableitungskurved'(t) = (2 t, 3 t² – 1), welche die Form einer Parabel hat.
- Anmerkung: x- und y-Koordinaten werden getrennt nach t abgeleitet!
- Man darf die Kurve und ihre Ableitungskurve nicht in dem Zusammenhang sehen, wie man es bei einem Funktionsgraphen und dem Graphen der Ableitungsfunktion kennt. Im Grunde genommen muss man zum einen die Ableitung in Abhängigkeit vom Parameter t sehen (und nicht x) und dann steht
d'(t)für den Richtungsvektor (vom Ursprung aus) in einem Punktd(t).
Anwendungsbeispiele[Bearbeiten]
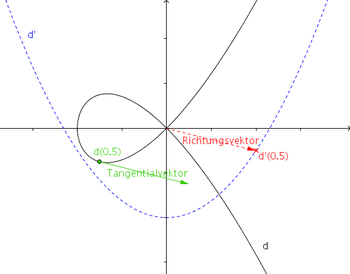
- Einzeichnen des Tangentialvektors an eine gegebene Kurve. Betrachten wir als Beispiel die schon verwendete Kurve:
d = Kurve[t² - 1, t (t² - 1), t, -5, 5]Ableitung[d]t=0.5... als Schieberegler sichtbar machen und Wertebereich -3 bis 3 einstellenP=d(t)... also hier zunächstd(0.5)⇒P = (-0.75, -0.38)Q=d'(t)Richtungsvektor=Vektor[(0, 0), Q]... siehe auch VektorTangentialvektor=Vektor[C,C+Richtungsvektor]
- Bewegt man nun den Schieberegler t, so wandert der Punkt auf der Kurve entlang und dazu der Tangentialvektor. Der Richtungsvektor und der Punkt Q können versteckt werden (siehe Sichtbarkeit).
- Vergleich der Tangentensteigung mit dem Ableitungswert um zu zeigen, dass die Ableitungsfunktion immer den Steigungswert der Tangenten an einer bestimmten Stelle liefert.
f(x)=x^2-2*xAbleitung[f]P=Punkt[f]a=Tangente[P,f]... siehe auch TangenteSteigung[a]x=x(P)... ergibt eine Senkrechte c durch den Punkt PS=Schneide[f',c]... unter Einstellungen als Beschriftung „Name & Wert“ auswählen.
- Man sollte noch die Farben etwas anpassen, damit man die Unterschiede besser erkennen kann, etwa die Ableitung rot einzeichnen und den Punkt S ebenso. Die Tangente sollte eine eigene Farbe bekommen. Bewegt man nun den Punkt P, so kann man erkennen, dass der y-Wert von S immer der Steigung der Tangenten entspricht.




