Diferencia entre revisiones de «Comando Superficie»

De GeoGebra Manual
m (Texto reemplazado: «;([a-zA-Z0-9]*)\[(.*)\]» por «;$1($2)») |
|||
| Línea 1: | Línea 1: | ||
<noinclude>{{Manual Page|version=5.0}}</noinclude><small>{{betamanual|version=5.0}}</small>{{Command|3D|Superficie}}{{GGb5D|1=<div> | <noinclude>{{Manual Page|version=5.0}}</noinclude><small>{{betamanual|version=5.0}}</small>{{Command|3D|Superficie}}{{GGb5D|1=<div> | ||
| − | ;Superficie | + | ;Superficie( <Ex<sub>pre<sub><small>sión</small></sub>></sub>, <Ex<sub>pre<sub><small>sión</small></sub></sub>>, <Ex<sub>pre<sub><small>sión</small></sub></sub>>, <Pará<sub><small>metro</small><sub><small>Variable 1</small></sub>></sub>, <Valor<sub><small>Inicial 1</small></sub>>, <Valor<sub><small>Final 1</small></sub>>, <Pará<sub><small>metro</small><sub><small>Variable 2</small></sub>></sub>, <Valor<sub><small>Inicial 2</small></sub>>, <Valor<sub><small>Final 2</small></sub>> ):Crea una superficie acorde a los valores indicados.<br>Establece la superficie Cartesiana '''3D'''(''imencional'') paramétrica para;<br>-la primera expresión en ''x'';<br>-la segunda, en ''y'';<br>-la tercera, en ''z''<br>... empleando sendas variables paramétricas dentro de los respectivos intervalos. Intervalos indicados entre uno y otro ''valor inicial'' y ''final''.</div>}} |
{{Examples|1=<br> | {{Examples|1=<br> | ||
:*<code><nowiki>Superficie[2 sen(t) * sen(v), sen(v), cos(v), t, 0, 2π, v, -π, π]</nowiki></code> crea la superficie asociada en la [[Vista 3D]]. | :*<code><nowiki>Superficie[2 sen(t) * sen(v), sen(v), cos(v), t, 0, 2π, v, -π, π]</nowiki></code> crea la superficie asociada en la [[Vista 3D]]. | ||
Revisión del 20:04 8 oct 2017
Superficie
Categorías de Comandos (todos)
- Superficie( <Expresión>, <Expresión>, <Expresión>, <ParámetroVariable 1>, <ValorInicial 1>, <ValorFinal 1>, <ParámetroVariable 2>, <ValorInicial 2>, <ValorFinal 2> )
- Crea una superficie acorde a los valores indicados.
Establece la superficie Cartesiana 3D(imencional) paramétrica para;
-la primera expresión en x;
-la segunda, en y;
-la tercera, en z
... empleando sendas variables paramétricas dentro de los respectivos intervalos. Intervalos indicados entre uno y otro valor inicial y final.
Ejemplos:
Superficie[2 sen(t) * sen(v), sen(v), cos(v), t, 0, 2π, v, -π, π]crea la superficie asociada en la Vista 3D.- Siendo r y R dos números de valores positivos reales:
Superficie[(R + r cos( u)) cos(v) , (R + r cos( u)) sen(v) , r sen(u ), u, 0, 2 π , v, 0, 2 π]crea el toro generado por un círculo de radio r cuyo centro rota en torno al EjeZ a la distancia R - Siendo desliz un deslizador entre 0 y 2 π, se puede ir desenvolviendo la construcción acorde al ritmo del cambio que se le imprima a
Superficie[(R + r cos( u)) cos(v) , (R + r cos( u)) sen(v) , r sen(u ),u,0,2 π , v,0, desliz]
Nota:
- El valor final debe ser mayor que el final y ambos deben ser finitos.
- ni x, ni y ni z se admiten como variables paramétricas.
Ejemplo:
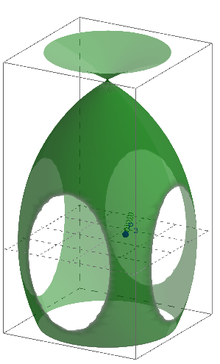
En la imagen puede apreciarse la superficie lateral derivada de uno de los ejemplos previos:
En la imagen puede apreciarse la superficie lateral derivada de uno de los ejemplos previos:
Superficie[(R + r cos( u)) cos(v) , (R + r cos( u)) sen(v) , r sen(u ),u,0,2 π , v,0, desliz]