Diferencia entre revisiones de «Comando Primero»

De GeoGebra Manual
| Línea 1: | Línea 1: | ||
| − | <noinclude>{{Manual Page|version= | + | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|cas=true|list|Primero}};Primero[ <Lista> ]:Da por resultado una nueva lista que solo contiene el primer elemento de la indicada. |
:{{Example|1='''<code>Primero[{1, 4, 3}]</code>''' da por resultado {1}.}} | :{{Example|1='''<code>Primero[{1, 4, 3}]</code>''' da por resultado {1}.}} | ||
:{{Note|1=Para obtener el primer elemento específicamente (el ''1'' y no la lista que lo contiene), puede emplearse el comando '''<code><nowiki>Elemento[{1, 4, 3}, 1]</nowiki></code>'''.}} | :{{Note|1=Para obtener el primer elemento específicamente (el ''1'' y no la lista que lo contiene), puede emplearse el comando '''<code><nowiki>Elemento[{1, 4, 3}, 1]</nowiki></code>'''.}} | ||
| Línea 15: | Línea 15: | ||
Las variantes '''aplicadas a listas''', que obran del modo ya descripto, admiten literales para operar simbólicamente. | Las variantes '''aplicadas a listas''', que obran del modo ya descripto, admiten literales para operar simbólicamente. | ||
:{{Example|1=Sin admitirlos directamente, el comando puede incorporar literales en la composición de operaciones simbólicas como en...<br><code>Primero[Último'''['''[[Comando Secuencia|Secuencia]]'''['''round(random()) [[Comando Exponencial|Exponencial]]'''['''round(random()),φ''']''' [[Comando PolinomioAleatorio|PolinomioAleatorio]]'''['''ñ-1,-3, 4''']''', ñ,3,5 ''']''',3''']''',2 ''']'''</code> da por resultado una lista aleatoria como, entre otras, la siguiente:<br><center><math>{ \left\{ \frac{-12 \textit{e}^{\varphi} x^{2} - 6 \textit{e}^{\varphi} x + 12 \textit{e}^{\varphi} + 12 x^{2} + 6 x - 12}{\textit{e}^{\varphi} }, 0 \right\} }</math></center>}} | :{{Example|1=Sin admitirlos directamente, el comando puede incorporar literales en la composición de operaciones simbólicas como en...<br><code>Primero[Último'''['''[[Comando Secuencia|Secuencia]]'''['''round(random()) [[Comando Exponencial|Exponencial]]'''['''round(random()),φ''']''' [[Comando PolinomioAleatorio|PolinomioAleatorio]]'''['''ñ-1,-3, 4''']''', ñ,3,5 ''']''',3''']''',2 ''']'''</code> da por resultado una lista aleatoria como, entre otras, la siguiente:<br><center><math>{ \left\{ \frac{-12 \textit{e}^{\varphi} x^{2} - 6 \textit{e}^{\varphi} x + 12 \textit{e}^{\varphi} + 12 x^{2} + 6 x - 12}{\textit{e}^{\varphi} }, 0 \right\} }</math></center>}} | ||
| − | + | ====Primeros Puntos en Ajuste==== | |
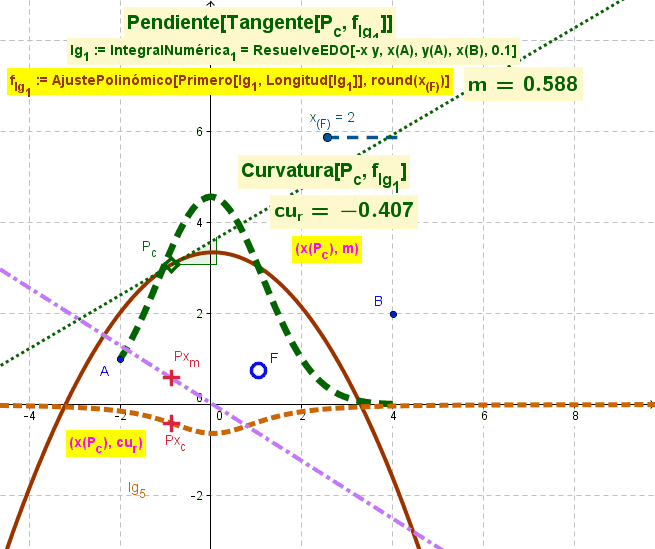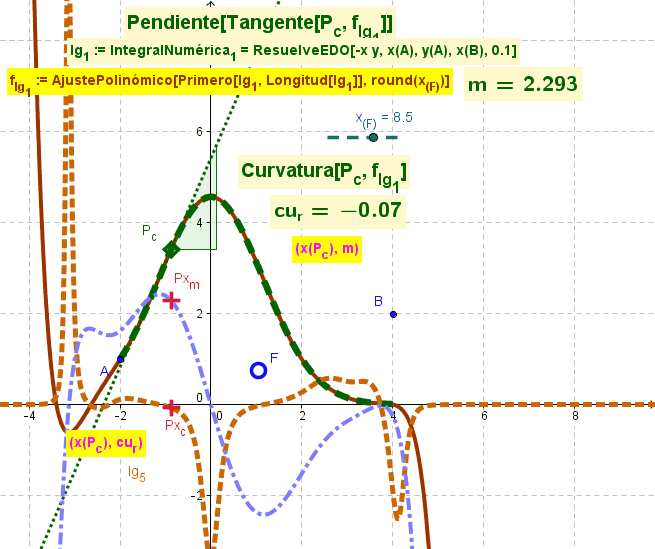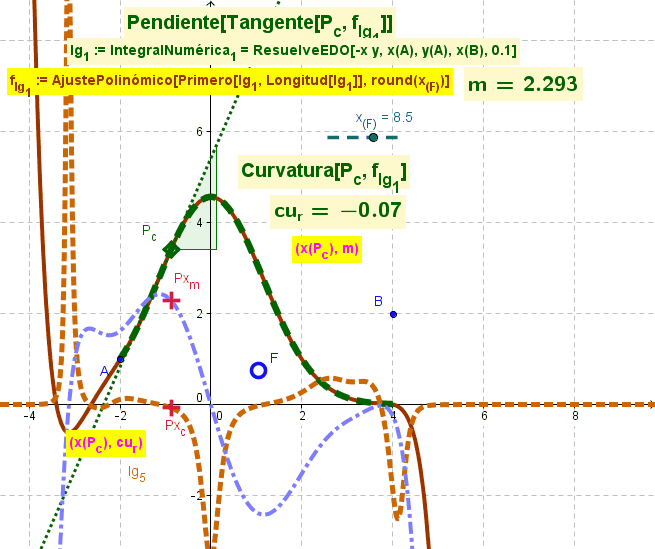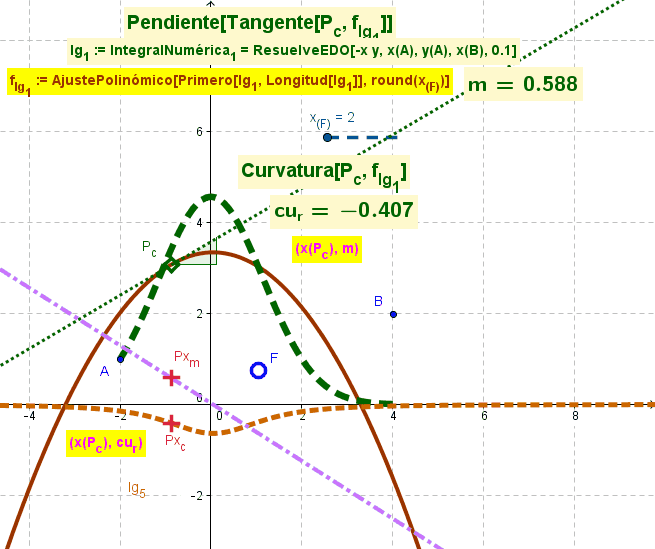
<hr><small>Se parte de una función surgida de un [[Comando AjustePolinómico|AjustePolinómico]] acotado por el valor del deslizador en marcha para tomar solo los '''''Primero'''s'' x_F puntos en ese [[Comando AjustePolinómico|AjustePolinómico]].<hr> | <hr><small>Se parte de una función surgida de un [[Comando AjustePolinómico|AjustePolinómico]] acotado por el valor del deslizador en marcha para tomar solo los '''''Primero'''s'' x_F puntos en ese [[Comando AjustePolinómico|AjustePolinómico]].<hr> | ||
[[Archivo:Curvatura y Pendiente lgs.gif|right]] | [[Archivo:Curvatura y Pendiente lgs.gif|right]] | ||
[[Comando AjustePolinómico|AjustePolinómico]] desde los puntos de un ''lugar geométrico'' representativo del [[Comando ResuelveEDO|ResuelveEDO]] (resolución de la ''ecuación diferencial ordinaria'');<br>'''<code>f_{lg_1} := AjustePolinómico[Primero[lg_1, Longitud[lg_1]], round(x_{(F)})]</code>'''<br></small><hr> | [[Comando AjustePolinómico|AjustePolinómico]] desde los puntos de un ''lugar geométrico'' representativo del [[Comando ResuelveEDO|ResuelveEDO]] (resolución de la ''ecuación diferencial ordinaria'');<br>'''<code>f_{lg_1} := AjustePolinómico[Primero[lg_1, Longitud[lg_1]], round(x_{(F)})]</code>'''<br></small><hr> | ||
:{{Note|1=Ver también el comando [[Comando Último|Último]].}} | :{{Note|1=Ver también el comando [[Comando Último|Último]].}} | ||
Revisión del 01:50 8 nov 2014
Primero
Categorías de Comandos (todos)
- Primero[ <Lista> ]
- Da por resultado una nueva lista que solo contiene el primer elemento de la indicada.
- Ejemplo:
Primero[{1, 4, 3}]da por resultado {1}. - Nota: Para obtener el primer elemento específicamente (el 1 y no la lista que lo contiene), puede emplearse el comando
Elemento[{1, 4, 3}, 1]. - Primero[ <Lista>, <número de los primeros n elementos> ]
- Da por resultado una lista que contiene exclusivamente los primerosn elementos de la dada.
- Ejemplos:
Primero[{1, 4, 3}, 2]establece la lista {1, 4}.
- Primero[ <Texto> ]
- Da por resultado el primer carácter del texto.
- Primero[ <Texto>, <Los n primeros elementos (número)> ]
- Da por resultado los n primeros caracteres del texto.
- Ejemplos:
Primero["yeso"]da por resultado el texto "y" que aparece en el centro de la Vista GráficaPrimero["Vela", 2]da por resultado el texto "Ve" que aparece en el centro de la Vista Gráfica.
- Primero[ <Lugar Geométrico>, <Los n primeros elementos (número)> ]
- Esta variante del comando resulta útil y adecuada para lugares geométricos generados por comandos como:
- ResuelveEDO - Da por resultado la lista de puntos que fueran creados en los n primeros pasos del algoritmo de resolución numérica EDO.
- MenorDistancia; Viajante u otros de trazados análogos (como Voronoi, ÁrbolRecubridorMínimo, CierreConvexo y Cierre) - Da por resultado la lista de los n primeros puntos vértices del correspondiente grafo.
- Ejemplo:
f_{lg_1} := AjustePolinómico[Primero[lg_1, Longitud[lg_1]], round(x_{(F)}) ]permite el AjustePolinómico de un lugar geométrico tomando sus primerosx_Fpuntos, acorde al valor de ese deslizador.
La figura al pie ilustra animadamente los resultados de ese ajuste de un lugar geométrico que provino del ResuelveEDO de una ecuación.
 En la Vista ComputaciónAlgebraicaSimbólica
En la Vista ComputaciónAlgebraicaSimbólica
Las variantes aplicadas a listas, que obran del modo ya descripto, admiten literales para operar simbólicamente.
- Ejemplo: Sin admitirlos directamente, el comando puede incorporar literales en la composición de operaciones simbólicas como en...
Primero[Último[Secuencia[round(random()) Exponencial[round(random()),φ] PolinomioAleatorio[ñ-1,-3, 4], ñ,3,5 ],3],2 ]da por resultado una lista aleatoria como, entre otras, la siguiente:{ \left\{ \frac{-12 \textit{e}^{\varphi} x^{2} - 6 \textit{e}^{\varphi} x + 12 \textit{e}^{\varphi} + 12 x^{2} + 6 x - 12}{\textit{e}^{\varphi} }, 0 \right\} }
Primeros Puntos en Ajuste
Se parte de una función surgida de un AjustePolinómico acotado por el valor del deslizador en marcha para tomar solo los Primeros x_F puntos en ese AjustePolinómico.
AjustePolinómico desde los puntos de un lugar geométrico representativo del ResuelveEDO (resolución de la ecuación diferencial ordinaria);f_{lg_1} := AjustePolinómico[Primero[lg_1, Longitud[lg_1]], round(x_{(F)})]
- Nota: Ver también el comando Último.