Diferencia entre revisiones de «Comando Weibull»

De GeoGebra Manual
m (Texto reemplazado: «;([a-zA-Z0-9]*)\[(.*)\]» por «;$1($2)») |
|||
| Línea 1: | Línea 1: | ||
<noinclude>{{Manual Page|version=5.0}}</noinclude>{{Command|cas=true|probability|Weibull}} | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{Command|cas=true|probability|Weibull}} | ||
| − | ;Weibull | + | ;Weibull( <Figura<sub>k</sub>>, <Escala<sub>λ</sub>>, x ):Establece y [[Vista Gráfica|grafica]], para los parámetros dados, la [[:w:es:Función_de_densidad_de_probabilidad|'''''fdp''''', <big>'''''f'''''</big>unción de '''''<big>d</big>'''''ensidad de <big>'''''p'''''</big>robabilidad]] (en inglés, [[:en:w:Probability_density_function|'''''p'''''robabilty '''''d'''''ensity '''''f'''''unction<sup><small>'''''pdf'''''</small></sup>)]] de la [[:w:es:Distribuci%C3%B3n_de_Weibull|''Distribución Weibull'']] ([[w:Weibull distribution|''Weibull distribution'']] en inglés) .<br>Así, '''Weibull[k, λ, x ]''' crea la ''fdp'' de una distribución de Weibull con parámetro de forma '''k''' y de escala '''λ'''. |
| − | ;Weibull | + | ;Weibull( <Figura<sub>k</sub>>, <Escala<sub>λ</sub>>, x, <Booleana<sub>Acumulativa</sub>> ):Si el valor ''booleano'' es falso<sup>''false''</sup>, establece y [[Vista Gráfica|grafica]], tomando '''x''' como variable, la <big>'''''f'''''</big>unción de '''''<big>d</big>'''''ensidad de <big>'''''p'''''</big>robabilidad de la distribución de Weibull y la acumulativa correspondiente en caso contrario. |
| − | ;Weibull | + | ;Weibull( <Figura<sub>k</sub>>, <Escala<sub>λ</sub>>, <Valor Variable> ):Calcula, para el valor asignado a la variable, el de la [[:w:es:Función de distribución_acumulada|'''''fda''''', función de distribución acumulativa]] de Weibull. |
:Así, '''Weibull[k, λ, v]''' establece la probabilidad ''P(X ≤ v)'' siendo ''X'' la [[:w:es:Variable_aleatoria|variable aleatoria]] de una distribución de Weibmull, con ''k'' y ''λ'' como parámetros y '''''v''''' el valor de la variable. | :Así, '''Weibull[k, λ, v]''' establece la probabilidad ''P(X ≤ v)'' siendo ''X'' la [[:w:es:Variable_aleatoria|variable aleatoria]] de una distribución de Weibmull, con ''k'' y ''λ'' como parámetros y '''''v''''' el valor de la variable. | ||
Revisión del 20:04 8 oct 2017
Weibull
Categorías de Comandos (todos)
- Weibull( <Figurak>, <Escalaλ>, x )
- Establece y grafica, para los parámetros dados, la fdp, función de densidad de probabilidad (en inglés, probabilty density functionpdf) de la Distribución Weibull (Weibull distribution en inglés) .
Así, Weibull[k, λ, x ] crea la fdp de una distribución de Weibull con parámetro de forma k y de escala λ.
- Weibull( <Figurak>, <Escalaλ>, x, <BooleanaAcumulativa> )
- Si el valor booleano es falsofalse, establece y grafica, tomando x como variable, la función de densidad de probabilidad de la distribución de Weibull y la acumulativa correspondiente en caso contrario.
- Weibull( <Figurak>, <Escalaλ>, <Valor Variable> )
- Calcula, para el valor asignado a la variable, el de la fda, función de distribución acumulativa de Weibull.
- Así, Weibull[k, λ, v] establece la probabilidad P(X ≤ v) siendo X la variable aleatoria de una distribución de Weibmull, con k y λ como parámetros y v el valor de la variable.
- Nota: Da por resultado la probabilidad para el valor de coordenada dada: área bajo la curva de la Distribución de Weibull, a la izquierda de la coordenada v dada.
 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
En esta vista obran de modo análogo al descripto ciertas variantes de sintaxisexcepto las de booleanas y se admiten literales para operar simbólicamente.
- Ejemplos:
Weibull[ 0.5, 1, 0]da 0Weibull[ 0.5, 1, 1]...
... desde la Barra de Entrada, establece en la Vista Algebraica 0.63 como resultado
... ingresado en la Vista CAS, da el valor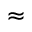 0.63decimales según Redondeo fijado y al evaluarlo
0.63decimales según Redondeo fijado y al evaluarlo 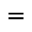 1 - \frac{ 1} { e } .
1 - \frac{ 1} { e } .Weibull[0.5, 1, x]da 0 parax < 0y en caso contrario, establece el siguiente resultado\frac{ ℯ^{\sqrt{x} } - 1 }{ℯ^{\sqrt{x} } } Weibull[0.5, 1, x, false]da 0 parax < 0y en caso contrario, establece el siguiente resultado\frac{ 1 }{2 \sqrt{x} ℯ^{\sqrt{x} } } Weibull[0.5, 1, x, x(A) > 0]desde la Barra de Entrada, establece en la Vista Algebraica, uno de los siguientes resultados.Resultado cuando la abscisa de A es menor o igual que 0
Abscisa de A mayor que 0
- Nota: Ver también el comando WeibullInversa
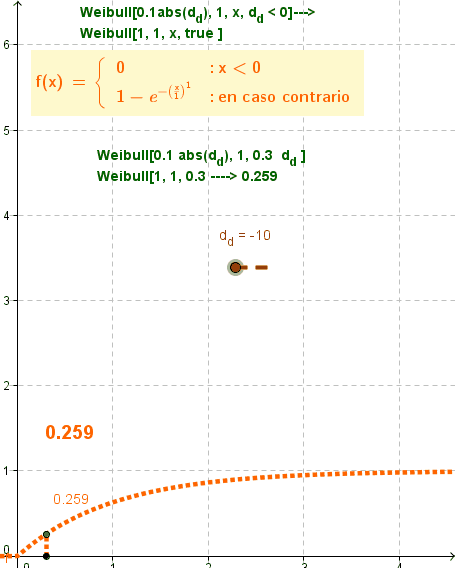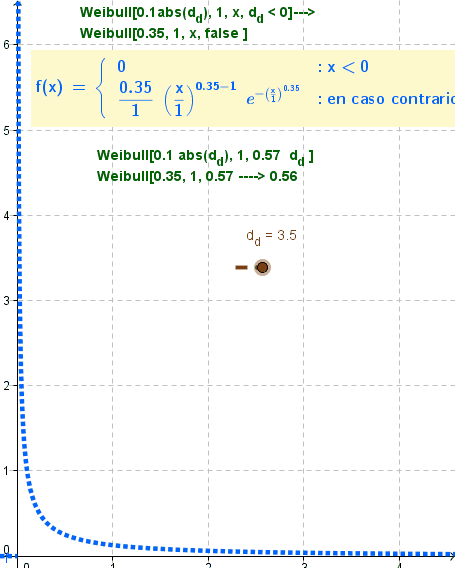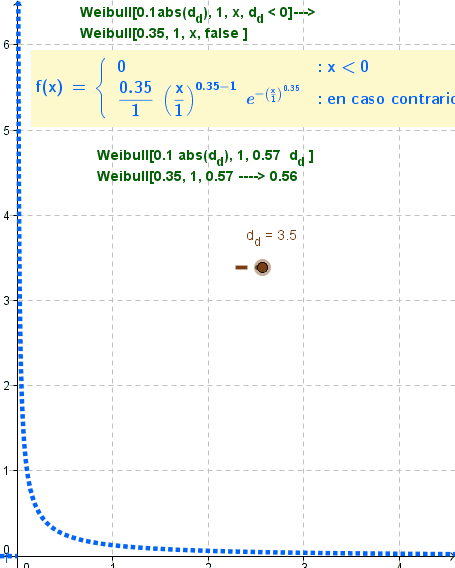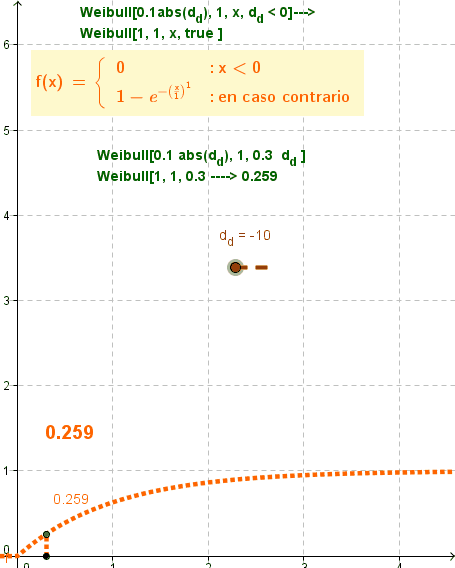
El boceto ilustra animadamente el comportamiento del comando a medida que cambian el valor booleano y el de un parámetro vinculado al deslizador.
Además del desenvolvimiento de la función, aparece el valor derivado del comando al que se le asignaran parámetros dependientes de los cambios del deslizador que, por otro lado, se ilustra como ordenada de la función, indicado en color naranja.