Comando Normal

De GeoGebra Manual
Normal
Categorías de Comandos (todos)
- Normal( <Media>, <Desviación estándar>, x )
- Crea la función de distribución acumulada de la distribución normal.
- Normal( <Media μ>, <Desviación estándar σ>, x, <Acumulada (true/false)> )
- Si Acumulada es verdadero, crea la función de distribución acumulada de la distribución normal de media μ y desviación σ, de lo contrario crea su función de densidad de probabilidad.
- Normal( <Media μ>, <Desviación estándar σ>, <Variable v> )
- Evalúa la función \Phi \left(\frac{x- \mu}{\sigma} \right) en v donde Φ es la función de distribución acumulada N(0,1) de media μ y desviación estándar σ.
- Nota: Devuelve la probabilidad para un valor dado de x (o el área bajo la curva de la distribución normal a la izquierda del valor dado de x).
- Ejemplo:
Normal(2, 0.5, 1)devuelve 0.02 en la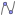 Vista Algebraica y \frac{erf(-\sqrt{2})+1}{2} en la
Vista Algebraica y \frac{erf(-\sqrt{2})+1}{2} en la  Vista CAS.
Vista CAS.




