Diferencia entre revisiones de «Comando CentroTriángulo»

De GeoGebra Manual
| Línea 1: | Línea 1: | ||
| − | <noinclude>{{Manual Page|version=4. | + | <noinclude>{{Manual Page|version=4.2}}</noinclude> {{command|cas=true|geometry|CentroTriángulo}} |
;CentroTriángulo[<Punto A>, <Punto B>, <Punto C>, <Indice n>]:Establece el e''n''ésimo [http://faculty.evansville.edu/ck6/encyclopedia/ETC.html centro triangular] del triángulo ''ABC''. Opera para n < 3054. | ;CentroTriángulo[<Punto A>, <Punto B>, <Punto C>, <Indice n>]:Establece el e''n''ésimo [http://faculty.evansville.edu/ck6/encyclopedia/ETC.html centro triangular] del triángulo ''ABC''. Opera para n < 3054. | ||
:{{Note|1=La numeración de los centros sigue el índice que puede consultarse, en inglés, en la [http://faculty.evansville.edu/ck6/encyclopedia/ETC.htm enciclopedia ETC referida], siendo el primero el ''incentro'', como se expone en la tabla que aparece a continuación.}} | :{{Note|1=La numeración de los centros sigue el índice que puede consultarse, en inglés, en la [http://faculty.evansville.edu/ck6/encyclopedia/ETC.htm enciclopedia ETC referida], siendo el primero el ''incentro'', como se expone en la tabla que aparece a continuación.}} | ||
Revisión del 21:45 1 may 2013
CentroTriángulo
Categorías de Comandos (todos)
- CentroTriángulo[<Punto A>, <Punto B>, <Punto C>, <Indice n>]
- Establece el enésimo centro triangular del triángulo ABC. Opera para n < 3054.
- Nota: La numeración de los centros sigue el índice que puede consultarse, en inglés, en la enciclopedia ETC referida, siendo el primero el incentro, como se expone en la tabla que aparece a continuación.
Algunos Centros Usuales
| Índice n | Centro |
|---|---|
| 1 | Incentro |
| 2 | Centroide |
| 3 | Circuncentro |
| 4 | Ortocentro |
| 5 | Centro en de la Circunferencia de Eulerde los nueve puntos |
| 6 | Punto de Symmedian |
| 7 | Punto de Gergonne |
| 8 | Punto de Nagel |
| 13 | Punto de Fermat |
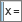 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
En esta vista, el comando obra del modo ya descripto.
- Ejemplo:
Secuencia[CentroTriángulo[M,N,Ñ,ñ], ñ, 1, 9]da por resultado la lista de los correspondientes primeros nueve puntos.
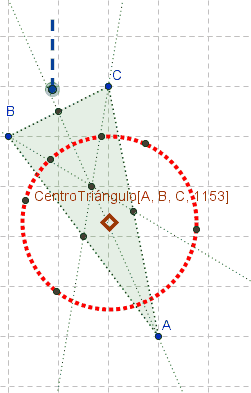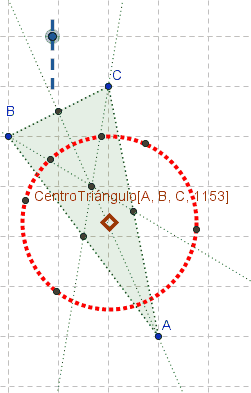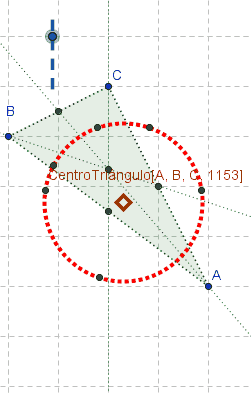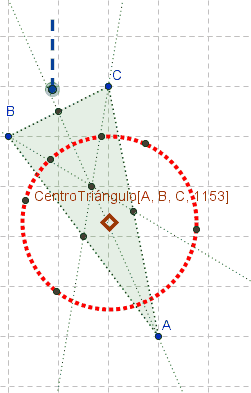
Al tildar el redondelito que encabeza la fila, cobra entidad algebraica y gráfica tal listado de puntos.  Atención: Las tres medianas de un triángulo ABC, lo dividen en seis triángulos con circuncentros cocíclicos en una circunferencia cuyo centro, como puede apreciarse animadamente en el boceto, se establece mediante:
Atención: Las tres medianas de un triángulo ABC, lo dividen en seis triángulos con circuncentros cocíclicos en una circunferencia cuyo centro, como puede apreciarse animadamente en el boceto, se establece mediante:CentroTriángulo[A, B, C, 1153]
- Nota: Ver también los comandos Trilineal, Cúbica y CurvaTriangular.