Visibilidad: de Condicional a Cuadrilateral

Visibilidad Condicional y Secuencias
Saltando de la Recta Numérica al Ámbito del Producto
El desafío de esta propuesta es tender un escenario para poder operar gráficamente desde las adiciones al producto. Como se emplearán una serie de herramientas y algunos comandos, es conveniente familiarizarse con su empleo antes de empezar.
Herramientas a tener a mano
| Deslizador | |
| Punto | |
| Vector | |
| Elige y Mueve | |
| Segmento | |
| Texto | |
| Casilla de Control |
Pasos de Construcción
1. Empezar por los ajustes iniciales:
- Desde el Menú Archivo, abrir una
 Nueva Ventana de GeoGebra.
Nueva Ventana de GeoGebra. - Escoger, en el Menú Apariencias alguna adecuada, como la de Álgebra y Gráficos o, si se va a simplificar el planteo, la de Geometría.
- Activar la Barra de Estilo de la
 Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
2. Un clic derecho sobre cualquier área libre de la ![]() Vista Gráfica para desplegar el Menú Contextual y pasar a abrir el Cuadro de Propiedades, dirigirse a la pestaña EjeY para fijar la Distancia en 1 (otro tanto, para el EjeX) y en Básico, fijar el mínimo de EjeX en -21 y el máximo en 21.
Vista Gráfica para desplegar el Menú Contextual y pasar a abrir el Cuadro de Propiedades, dirigirse a la pestaña EjeY para fijar la Distancia en 1 (otro tanto, para el EjeX) y en Básico, fijar el mínimo de EjeX en -21 y el máximo en 21.
3. Crear...
- los deslizadores a y b (de intervalos entre -10 y 10 e incremento 1) de modo que se exponga en cada caso un rotulado de su Valor respectivo en lugar de sus nombres (acudiendo al Cuadro de Propiedades).
- con la
 herramienta correspondiente, el punto A sobre el EjeX y ubicarlo, inicialmente en el origen de coordenadas.
herramienta correspondiente, el punto A sobre el EjeX y ubicarlo, inicialmente en el origen de coordenadas. - anotándolos en la Barra de Entrada...
- los vectores
- u = Vector((x(A), y(A) + 1), (x(A) + a, y(A) + 1)) que tendrá longitud a
- v = Vector((x(A) + a, y(A) + 2), (x(A) + a + b, y(A) + 2)) que tendrá longitud b
- los segmentos:
- Segmento(A, (x(A), y(A) + 1));
- Segmento((x(A) + a, y(A)), (x(A) + a, y(A) + 1));
- Segmento((x(A) + a, y(A)), (x(A) + a, y(A) + 2)),
- Segmento((x(A) + a + b, y(A)), (x(A) + a + b, y(A) + 2)) asignándoles estilo punteado y los mismos colores de los vectores cuyos extremos señalan.
- el punto B = A + u + v
 Aviso: x(A) es la abscisa del punto A e y(A). su ordenada por lo que el punto B, en que interviene vectores que se definen sumando los valores de b y/o a' a x(A) tendrá una abscisa acorde al resultado de la suma, como se puede corroborar tras el análisis correspondiente.
Aviso: x(A) es la abscisa del punto A e y(A). su ordenada por lo que el punto B, en que interviene vectores que se definen sumando los valores de b y/o a' a x(A) tendrá una abscisa acorde al resultado de la suma, como se puede corroborar tras el análisis correspondiente.
- los vectores
4. Abrir el Cuadro de Propiedades para ajustar la construcción (cambiando los colores, estilos, ancho de los deslizadores, ocultado o exponiendo rótulos, por ejemplo).
Un toque de texto dinámico
Para realzar el escenario interactivo, se le suma, con la correspondiente herramienta ![]() , texto dinámico que ilustre los cálculos de sumas.
, texto dinámico que ilustre los cálculos de sumas.
4. Calcular el resultado del cálculo de la suma: r = a + b e ilustrarlo con colores diferentes y contrastantes para lo que es preciso insertar, uno a uno con la ![]() adecuada, cada componente de la suma:
adecuada, cada componente de la suma:
- Seleccionándolos desde Objetos...
- a (que devendrá texto_1), al que posteriormente, con la correspondiente
 , se le copiará el estilo visual de a - para asignarle el mismo color -
, se le copiará el estilo visual de a - para asignarle el mismo color - - b y r que establecerán un texto independiente y a los que se los someterá a la misma maniobra que al anterior pero asociados a b y r respectivamente.
- a (que devendrá texto_1), al que posteriormente, con la correspondiente
 Atención:
Atención:
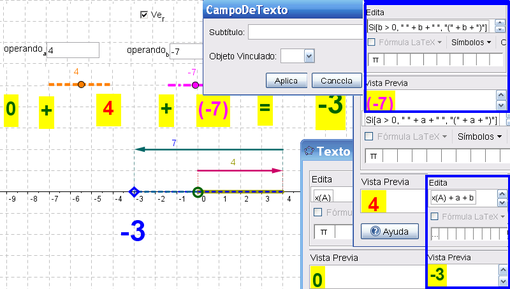
Si se quisiera evitar la creación del nuevo objeto, r, es posible resolverlo sobre la misma edición del texto a insertar.
Basta con anotar en tercer lugar nuevamente el objeto a o el b y luego, ingresar con el cursor dentro del recuadro punteado que lo enmarca y a continuación de la a o antes de la b, añadir + b o a + según sea el caso.
Otra alternativa sería ingresar como objeto indicador del resultado al punto B y editarlo para que pase a ser x(B).
Si se quisiera tomar en cuenta el valor de la posición de partida en esta operación, como se verá más adelante, también habrá que anteponer x(A) +.
- Anotándolos directamente:
- entre el texto de a y el de b, el signo +
- el = entre el de b y el del resultado.
5. Dar a los textos la medida de tipografía adecuada, desde la Barra de Estilo de la ![]() Vista Gráfica y, de ser preciso, acudir al Cuadro de Propiedades para fijar los textos y establecer que el Rotulado de cada deslizador se limite a su Valor.
Vista Gráfica y, de ser preciso, acudir al Cuadro de Propiedades para fijar los textos y establecer que el Rotulado de cada deslizador se limite a su Valor.
Ajustes y Contrastes Ilustrativos
6. Ajustar algunos detalles revisando que...
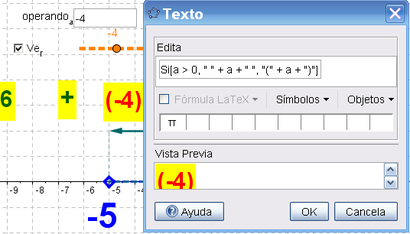
- cuando tanto a como b son negativos, el aspecto de la operación cuyo texto dinámico se expone resulta inadecuado.
 Atención: En tanto requiere de paréntesis en tales casos, conviene convertir el objeto a ser expuesto de numérico a textual con una maniobra como la que se ilustra a continuación.
Atención: En tanto requiere de paréntesis en tales casos, conviene convertir el objeto a ser expuesto de numérico a textual con una maniobra como la que se ilustra a continuación.
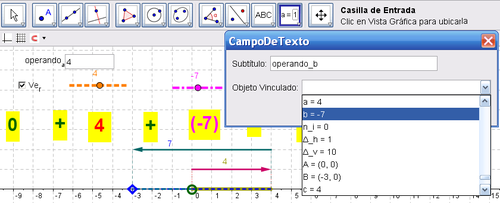
- puede ser más cómodo anotar los valores de cada operando desde casillas de entrada a crear con la herramienta
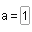 de Casilla de Entrada y asociarse a a y b, respectivamente.
de Casilla de Entrada y asociarse a a y b, respectivamente.  Atención: Es conveniente ajustarle a ambas cada Longitud de la Casilla de Entrada en la pestaña Estilo del Cuadro de Propiedades
Atención: Es conveniente ajustarle a ambas cada Longitud de la Casilla de Entrada en la pestaña Estilo del Cuadro de Propiedades
- cuando el punto A se desplaza, el valor del resultado de la operación no concuerda con r
- es conveniente que cada operador contraste con el color que se le puede adjudicar al fondo con una simple maniobra en la Barra de Estilo, como se expone en la figura que aparece en la sección posterior.
7. Exportar este escenario dinámico e interactivo.
Al ver... verás
¡Verás!
Es conveniente incluir un recurso de control para que sea el resultado o uno u otro de los operandos resulte visible o se oculte, acorde se tilde o no la ![]() casilla a tal efecto creada con la herramienta correspondiente.
casilla a tal efecto creada con la herramienta correspondiente.
Condicional para Ocultar/Mostrar vía Casillas de Control
Pasos de Construcción
Para insertar una ![]() Casilla de Control para Ocultar/Mostrar Objetos en la
Casilla de Control para Ocultar/Mostrar Objetos en la ![]() Vista Gráfica que permita controlar si va a mostrarse o no el resultado y los indicios o indicadores asociados, tendrá que afectar a todos los componentes:
Vista Gráfica que permita controlar si va a mostrarse o no el resultado y los indicios o indicadores asociados, tendrá que afectar a todos los componentes:
- el texto del resultado
- el punto cuya abscisa corresponde al resultado
- el segmento que ilustra el tramo asociado al resultado
Para lograrlo, basta con:
- Apelar a la herramienta
 Casilla de Control para Ocultar/Mostrar Objetos, seleccionándola y señalando con un clic en la
Casilla de Control para Ocultar/Mostrar Objetos, seleccionándola y señalando con un clic en la  Vista Gráfica, la posición en que quedará ubicada
Vista Gráfica, la posición en que quedará ubicada - Anotarle un adecuado Subtítulo, como Ver_r
- Seleccionar los objetos a afectar, sea en la
 Vista Gráfica. con un clic, o indicándolos en la lista desplegable que permite escogerlos.
Vista Gráfica. con un clic, o indicándolos en la lista desplegable que permite escogerlos. - Confirmar pulsando sobre 'Aplica que se completó la maniobra
- Controlar, tildando la casilla y des-tildando' la casilla, que responden a la maniobra todos los objetos que deben afectarse
- Fijar la casilla si se lo considera preciso, desde el Cuadro de Propiedades
- Subsanar alguna posible omisión de alguno de los objetos que debieran afectarse, seleccionándolos y anotando el nombre - no el Subtítulo - de la casilla en el campo Condición para Exponer el Objeto de la pestaña Avanzado' del correspondiente Cuadro de Propiedades.
- Revisando el comportamiento adecuado.
- Añadir algunos deslizadores para asignar objetivos en desafíos por llegar, de distintos modos a tal resultado, que es un reto de mayor nivel que el de calcularlo.
- Concluir, exportando el boceto resultante añadiendo, acaso, otros desafíos exploratorios.
Variables Booleanas
El ![]() casillero de control para mostrar u ocultar Objetos no es sino una representación gráfica de una variable lógica o Booleana que, como tal, puede tener dos valores de verdad:
casillero de control para mostrar u ocultar Objetos no es sino una representación gráfica de una variable lógica o Booleana que, como tal, puede tener dos valores de verdad:
- cierto (true en inglés), cuando la casilla está tildada o
- falso (false en inglés) cuando no lo está.
Cada uno de los objetos afectados por este control, mostrará en el campo Condiciones para Exponer el Objeto de la pestaña Avanzado del Cuadro de Propiedades, el nombre asignado a la casilla - no su Subtítulo - que es el de la variable Booleana.
Si los segmentos punteados que evidencian los extremos del segmento de resultado no hubieran sido incluidos inicialmente, pueden serlo ahora, a través de la maniobra de anotar el nombre de la variable en tal campo.
Se podría hacer más compleja la condición en situaciones en que se deseara que un objeto de texto - como "Resultado Negativo" por ejemplo - quedara o no expuesto. En este caso, se anotaría algo como esto en el campo de condición de visibilidad:
x(A) + a + b < 0
El Triángulo de Sierpinski
¿Cómo agilizar la creación de un triángulo como el que se ilustra? ¿Acaso con ayuda de una herramienta propia especialmente preparada para la tarea?
Preparativos
- Desde el Menú Archivo, abrir una
 Nueva Ventana de GeoGebra.
Nueva Ventana de GeoGebra. - Escoger, en el Menú Apariencias alguna adecuada, como la de Álgebra y Gráficos o, si se va a simplificar el planteo, la de Geometría.
- Activar la Barra de Estilo de la
 Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Pasos de Construcción
| 1 | Crear un triángulo cualquiera, ABC. | |
| 2 | Cambiarle el color, con la maniobra adecuada en la Barra de Estilo. | |
| 3 | Establecer el Punto Medio D del lado AB, el E del lado BC y F el de AC. | |
| 4 | Construir el triángulo DEF. | |
| 5 | Cambiarle el color a DEF, con la maniobra adecuada en la Barra de Estilo y con una opacidad del 100%. | |
| 6 | Crear una nueva herramienta denominada Sierpinski.
Los objetos de salida serán los puntos D, E y F, el triángulo DEF, y sus lados Los objetos de entrada serán los puntos A, B y C Nombre: Sierpinski Ayuda de la Herramienta: Clic en tres puntos | |
| 7 | Aplicar la nueva herramienta sobre cada triángulo esbozado recientemente - ADF, DBE y FEC - para avanzar hacia la segunda etapa del triángulo de Sierpinski. | |
| 8 | Avanzar del mismo modo, hacia la tercera etapa. |
Visibilidad Condicional
Crear tres casillas de control de visibilidad para cada una de las etapas de desenvolvimiento del triángulo de Sierpinski.
Introducción a Secuencias
GeoGebra ofrece un comando de gran potencia para producir listas de objetos del mismo tipo, cuya cantidad y 'distanciamiento determinan sus parámetros en adecuada sintaxis:
- Secuencia( <expresión>, <variable>, <desde>, <hasta>, <distanciamiento> ) donde...
- <expresión>: Establece el tipo y proceso de producción de los objetos que compondrán la lista resultante en relación a la variable de evolución, dentro del rango fijado (como (i, 0) siendo la variable i).
- <variable>: Indica el nombre de la variable en juego* <desde>, <hasta>: Establecer el intervalo empleado para el desenvolvimiento de la variable (desde 1 hasta 100, el rango es justamente, el de esa centena).
- <distanciamiento>: Opción que determina la dimensión del paso de una unidad de la variable a la siguiente que, por omisión es 1.
- Secuencia( (n, 0), n, 0, 10)
- Crea, a lo largo del eje-x, una lista de 11 puntos de las siguientes coordenadas (0, 0), (1, 0), (2, 0), …, (10, 0).
- Secuencia(Segmento((a, 0), (0, a)), a, 1, 10, 0.5)
- Crea una lista de segmentos de longitud creciente, separados por 0.5 unidades de distancia.
- Cada segmento une un punto en el eje x con uno del eje y de coordenadas recíprocas como el (1, 0) con (0, 1); (2, 0) con (0, 2)...
- Secuencia((i, i), i, 0, s) - siendo s el valor de un deslizador que opera en el intervalo de 1 a 10 con un incremento igual a 1 -, crea una lista de s + 1 puntos - de coordenadas (0, 0), (1, 1), …, (10, 10)- cuya longitud puede variar dinámicamente cuando se arrastra s.
Producto Visual de Números Naturales
Preparativos
- Desde el Menú Archivo, abrir una
 Nueva Ventana de GeoGebra.
Nueva Ventana de GeoGebra. - Escoger, en el Menú Apariencias alguna adecuada, como la de Álgebra y Gráficos o, si se va a simplificar el planteo, la de Geometría (en ese caso, acudir al Menú Vista para que quede expuesta la Barra de Entrada).
- Activar la Barra de Estilo de la
 Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Pasos de Construcción
| 1 | Establecer los deslizadores numéricos - señalando Entero - de Ancho 300, que opere en el Intervalo de 1 a 10 con un Incremento igual a 1...
| |
| 2 | Crear el punto A, ubicándolo en el origen de coordenadas. | |
| 3 | Determinar cuatro puntos, derivados de A, anotando en la Barra de Entrada:
| |
| 4 | Desplazar el deslizador Columnas y el de Filas para controlar el comportamiento acorde de los puntos recién creados. | |
| 5 | Trazar el polígono ABDC. | |
| 6 | Crear dos listas una de segmentos verticales y otra de horizontales.
Nota: A + k (1, 0) especifica una serie de puntos que empiezan en A con distancia 1 entre uno y otro y C + k (1, 0), la de los que se inician en C y se distribuyen horizontalmente a la misma distancia - B + k (0, 1)] desde B y con distribución vertical -. Segmento[A + k (1, 0), C + k (1, 0)] crea una lista de segmentos entre estos pares de puntos. De modo similar se distribuyen los segmentos determinados por la siguiente Secuencia | |
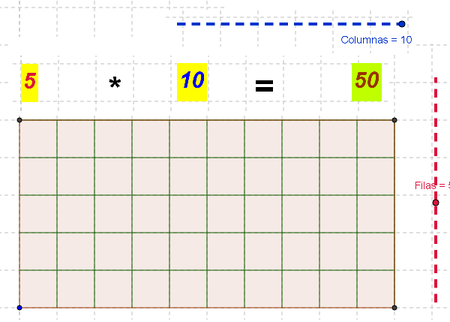
| 7 | Insertar los correspondientes textos, estáticos y dinámicos que ilustran y especifican los cálculos de multiplicación que tienen como factores los valores de los deslizadores Columnas y Filas:
texto1: Columnas texto2: * texto3: Filas texto4: = | |
| 8 | Calcular el resultado del producto de Columnas * Filas | |
| 9 | Inserta el dinámico texto5: resultado | |
| 10 | Ocultar los puntos A, B, C y D. | |
| 11 | Ajustar y mejorar la construcción a partir de las posibilidades que ofrecen la Barra de Estilo o, de ser preciso, el Cuadro de Propiedades |
Reto Artístico vía Curvas de Bézier
Las curvas de Bézier son una de las paramétricas que suelen emplear los utilitarios de graficación para trazar curvas o modificar vectorialmente', la medida de la tipografía. En este escenario, se creará un tendido de hilos para poder trazar curvas de Bézier con fines artístico-ornamentales.
Preparativos
- Desde el Menú Archivo, abrir una
 Nueva Ventana de GeoGebra.
Nueva Ventana de GeoGebra. - Escoger, en el Menú Apariencias alguna adecuada, como la de Álgebra y Gráficos o, si se va a simplificar el planteo, la de Geometría (en ese caso, acudir al Menú Vista para que quede expuesta la Barra de Entrada).
- Activar la Barra de Estilo de la
 Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Vista Gráfica para dar visibilidad a la Cuadrícula' y establecer la condición Ajusta a Cuadricula y en cuanto al Rotulado, limitarlo a Solo puntos nuevos.
Pasos de Construcción
Se detallará la modalidad de construcción paso a paso, si bien es posible crear el diseño partiendo solo de tres puntos - A, B y C -, anotando en la Barra de Entrada el siguiente anidado' de comandos:
- lis_B = Secuencia(Segmento(Elemento(Secuencia(A + k / n (B - A), k, 1, n), i), Elemento(Secuencia(A + k / n (C - A), k, 1, n), n - i)), i, 1, n)
| 1 | Trazar...
| |
| 2 | Crear un deslizador n numérico - Entero - de Ancho 200 con Incremento 1 e intervalo extendido de 0 a 50. | |
| 3 | Establecer, desde la Barra de Entrada las secuencias... | |
| 4 | Ocultar sendas listas de puntos. | |
| 5 | Crear una lista de segmentos...
| |
| 6 | Ajustar y menorar el aspecto de la construcción apelando a los recursos que habilita la Barra de Estilo y/o apelando al Cuadro de Propiedades | |
| 7 | Desplazar los puntos A, B y C para cambiar el aspecto y dorma de la curva de Bézier. | |
| 8 | Modificar el valor que, a expensas del deslizador, establece el de n para cambiar el número de segmentos que crea la curva de Bézier. |
Desafío Adicional
Acaso, podríamos plantear:
- además de encontrar los puntos que en el trazado previo permiten un Ajuste que se acerque al trazado de las curvas que lo inspiraron...
- ...el más abierto a crear más arte hilado empleando secuencias de puntos y segmentos con GeoGebra.
Los puntos de aparente intersección que se podría creer permitirían establecerse para intentar algún tipo de ajuste (como el polinómico, no son objetos accesibles.
No lo son, dado que cada uno de los segmentos trazados no tiene entidad directa sino como elementos de una lista.
Por eso, se requiere una maniobra en que es preciso apelar al comando Elemento para hacer viable la producción de cada intersección.
Cuadrilateando
A lo largo de esta propuesta, clásica de Centro Babbage, conviene ir produciendo, paso a paso, la construcción del planteo en la Ventana de GeoGebra.
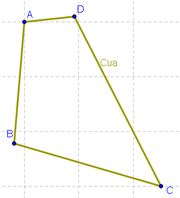
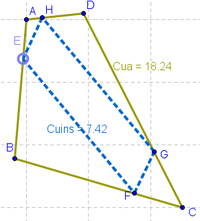
1 Empleando la Herramienta de Polígono, construimos un cuadrilátero cualquiera con vértices en los puntos A, B, C y D respectivamente (recordando volver a dar clic sobre el punto inicial A para "cerrar" el polígono). Para su mejor identificación, se activa el Menú Contextual, apelando a la alternativa desde la que se lo Renombra Cua.
2 Con la Herramienta de Punto, creamos uno, E, sobre el segmento de lado que une los puntos A y B.
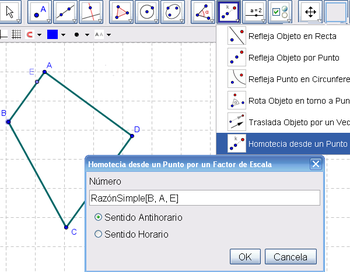
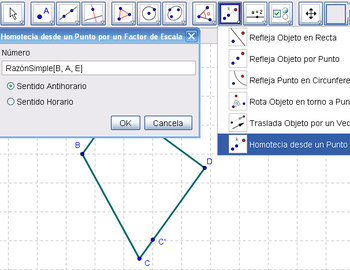
3 Empleando la Herramienta de Homotecia pasamos a crear otro punto en el lado opuesto al que une A y B, el tendido entre C y D, para obtener el resultado de la Homotecia(C, RazónSimple(B, A, E), D).
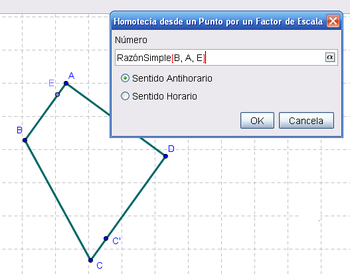
4 Otro tanto para crear la Homotecia(C, RazónSimple(B, A, E), B) sobre el lado que une A y D.
5 Del mismo modo para fijar la Homotecia(A, RazónSimple(B, A, E), D) en el lado que une D y A.
De este modo se completa el trazado de los cuatro puntos en cada lado...
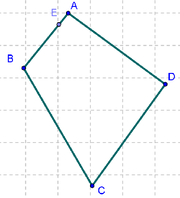
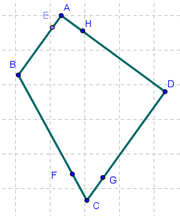
6 Volvemos a apelar a la Herramienta de Polígono para crear el que une cada uno de los puntos recién creados sobre cada lado.
7 Es sencillo notar que todos los vértices del cuadrilátero A, B, C, D son libres y que al desplazarlos se modifica el tipo de cuadrilátero que acabamos de "inscribir" en Cua (el de ABCD).
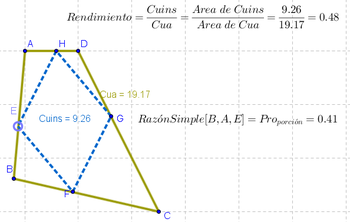
8 Para mayor claridad a este cuadrilátero que une a los vértices EFGH, se lo Renombra Cuins y se destaca con diferente estilo a su único punto desplazable, el E. Apelando al Cuadro de Propiedades, se establece que de sendos cuadriláteros se expondrán tanto sus rótulos como sus valores de modo que se pueda apreciar rápidamente el modo en que se relacionan.
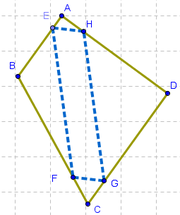
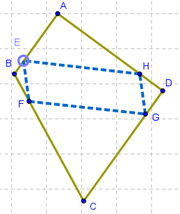
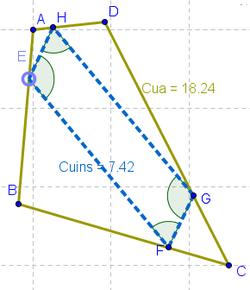
9 Podemos notar que al desplazar el punto E, los que de E dependen, ubicados sobre cada lado de ABCD, concuerdan con su movimiento para seguir ocupando la misma posición proporcional en los correspondientes lados de ABCD.. Si procuramos llevar E al punto medio entre A y B, otro tanto resultará con los vértices del "inscripto" en sus respectivos lados. Si se lo lleva hasta cerca de la novena parte de uno de los vértices del lado que ocupa, otro tanto sucederá con los demás vértices, F, G y H.
Cuadrilátero Cuins cuyos vértices son puntos que ocupan la misma posición proporcional en cada lado de Cua.
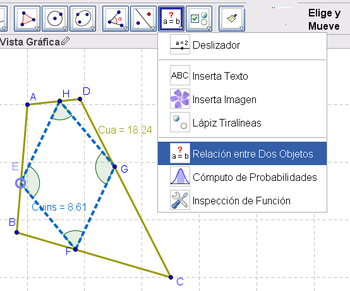
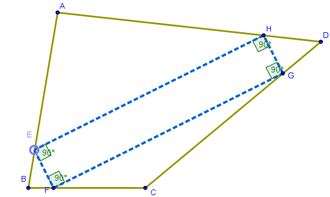
10 Para identificar con mayor facilidad las propiedades del cuadrilátero Cuins, se acude a la Herramienta de Ángulo que se le aplica en una maniobra simple.
11 Para explorar con un propósito guía que conduzca las observaciones, podemos plantearnos y/o plantearles a los estudiantes, una serie de desafíos. Por ejemplo...
- ¿Cómo harían para que el "inscripto" resulte un rombo o un cuadrado, lo primero que puedan lograr? o
- ¿Cómo creen que podría lograrse que llegara a configurar un trapecio o a un rectángulo?.
Algunas de las maniobras podría llevar a algún logro, al menos según se lo pudiera apreciar a simple vista y, en tal caso, sería importante cuestionarse sobre cómo controlar con mayor rigor, acudiendo a la Herramienta de Relación y/o a la información complementaria que ofrece la ![]() Vista Algebraica.
Vista Algebraica.
En cada ocasión, valdría analizar las condiciones que se procuraron para cada logro para poder reproducirlo sin necesidad de volver a tanteos que, en todo caso, se facilitan poniendo a la Vista la Cuadrícula y activando la alternativa Ajusta a Cuadrícula a partir de la Opción que establece la Atracción de Punto a Cuadrícula.
12 Los interrogantes que en el camino de las exploraciones pueden reiterarse apuntan a...
- ¿Cómo controlar que se llega a cada una de las metas propuestas? y
- ¿Qué herramientas conviene emplear y qué relaciones verificar?
- El método que se emplee para lograr cada uno de los cuadriláteros de distinto tipo, ¿será el único?
- ¿Será válido en todos los casos?
- ¿Cómo podríamos asegurarlo?
- ¿Habrá algunas metas imposibles de lograr?
- ¿Cómo podríamos convencernos de esta eventual imposibilidad?
13 Respecto, ya no de las posibles clasificaciones vinculadas a procedimientos acorde a propiedades de Cuins en relación a Cua, sino al régimen de cambio de las relaciones entre sus respectivas áreas, un planteo a indagar podría ser: ¿Cómo conseguir el máximo rendimiento de modo que al recortar el cuadrilátero inscripto Cuins se minimice el desperdicio de los "recortes" sobrantes de Cua?.
Incluso, ¿Cómo conseguir un rendimiento de un tercio del máximo posible?. Este tipo de interrogante incluye la necesidad de establecer, además, cuál es el máximo rendimiento.
Para llevar adelante esta indagación conviene establecer tanto la razón de las áreas como la de la proporción en que cada vértice de Cuins divide al correspondiente lado de Cua.
Además de recurrir a la ![]() Vista Algebraica para ir recabando esa información (una vez que se hizo el ingreso de los cálculos en la Barra de Entrada), es conveniente incluirla en la
Vista Algebraica para ir recabando esa información (una vez que se hizo el ingreso de los cálculos en la Barra de Entrada), es conveniente incluirla en la ![]() Vista Gráfica empleando la Herramienta de Texto.
Vista Gráfica empleando la Herramienta de Texto.
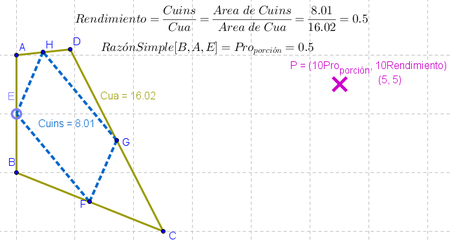
14 Para indagar de modo más completo el posible régimen de relaciones y de cambios entre la RazónSimple en juego y la razón entre sendas áreas, conviene establecer un punto de definición algebraica, ingresando en la Barra de Entrada, los valores variables de sus coordenadas como (10Pro_{porción}, 10Rendimiento) siendo Pro_{porción} la RazónSimple y Rendimiento la que se establece entre las áreas de Cuins a Cua.
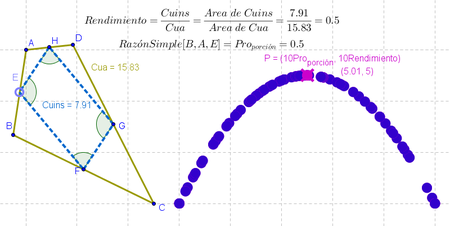
15 El modo preliminar de controlar cómo varía el Rendimiento en función de la Pro_{porción}, sería facilitar el registro en tanto se le Activa Rastro al punto de definición algebraica recién creado, tildando esta alternativa de su Menú Contextual, emergente cuando se lo selecciona y se pulsa el botón derecho del ratón o mouse.
Rastro que aparece a medida que se desplaza el punto E, vértice de Cuins, por el lado que ocupa en Cua.
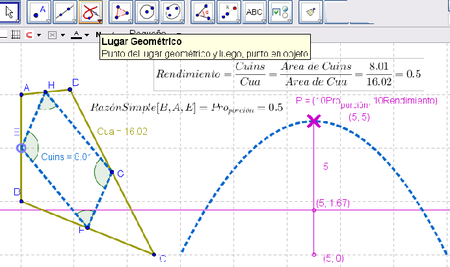
16 Es más perdurable y susceptible de mejor análisis que el rastro del punto de definición algebraica a medida que se desplaza E, el lugar geométrico correspondiente.
Los primeros cálculos pueden operarse sobre el lugar geométrico y, a medida que se progresa en su análisis, se pueda considerar con qué tipo de cónica pudiera tal trazo coincidir, apelando a la correspondiente herramienta y/o recabando los valores del punto en juego en la Hoja de Cálculo.
Esta multiplicidad de representaciones simultáneas permite un estudio de peculiar riqueza del régimen de relaciones y del de variaciones a partir de cada posible "punto de Vista".