Lignes

Les outils "Lignes" sont, par défaut, regroupés sous l'icône ![]() (3ème gauche) dans la Barre_d'outils
(3ème gauche) dans la Barre_d'outils
Ils sont présentés différemment dans la Barre_d'outils suivant que la fenêtre Graphique 3D soit active ou non.
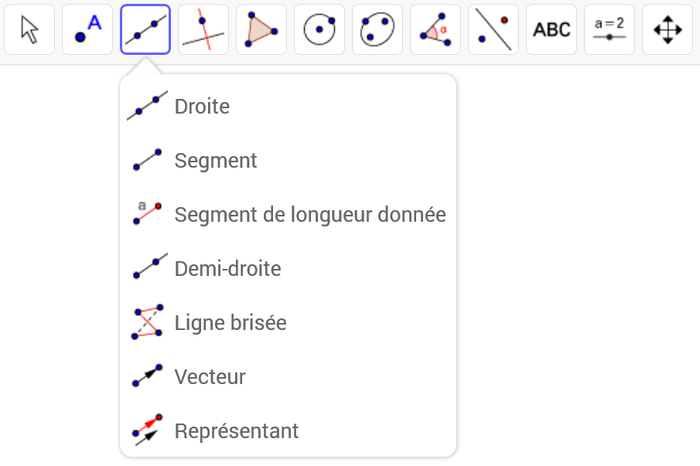
Actuellement, il y a sept outils "Lignes" (mais ![]() Ligne brisée , n'est pas utilisable dans la fenêtre Graphique 3D) :
Ligne brisée , n'est pas utilisable dans la fenêtre Graphique 3D) :
| Graphique (1 ou 2) active | Graphique 3D active | ||
|---|---|---|---|
| Droite | Droite | ||
| Segment | Segment | ||
| Segment de longueur donnée | Segment de longueur donnée | ||
| Demi-droite | Demi-droite | ||
| Ligne brisée | Vecteur | ||
| Vecteur | Représentant | ||
| Représentant | |||
Équations de droites :
Pour l'équation d'une droite
- en Graphique 2D il a 4 écritures possibles :
y = ax + b ;
ax + by = c ;
ax + by + c = 0 et
paramétrique X = A + λ \overrightarrow{AB}
- en Graphique 2D il a 4 écritures possibles :
ainsi les saisies y=2x-3, 2x-y=3, 2x-y-3=0 et X=(0,-3)+λ (1,2) construiront la même droite (bon ... GeoGebra modifiera la dernière équation en X=(1.5,0)+λ (1,2))
 Attention:
Attention: Ne pas oublier de mettre une espace entre λ et le vecteur directeur choisi
- en Graphique 3D il n'y a que l'écriture paramétrique X = A + λ \overrightarrow{AB}.
ainsi la saisie X=(1,1,1)+ λ (1,2,3) construira une droite dans Graphique 3D.
Mais aussi depuis la version 332, avant le brexit, vous pouvez utiliser une syntaxe utilisée de l'autre côté du channel
la saisie x-1=y-2=(z-3)/2 (qui sera transformée en définition en IntersectionChemins[x-1+0z=y-2,x-1=(z-3)/(2)])
construira la droite d'équation f: X = (-0.58, 0.42, -0.17) + λ (0.5, 0.5, 1)
ayant pour description "Droite d'intersection de x-1+0z=y-2 et x-1=(z-3)/2"
la saisie r=(2+3t) (1,0,0)+(4+3t) (0,1,0) +(7+t) (0,0,1) ou plus simplement (2+3t,4+3t,7+t)
construit la droite d'équation paramétrique X = (2, 4, 7) + λ (3, 3, 1)
4 saisies différentes pour une même droite de Graphique 3D
IntersectionChemins[4x+7y=46,y+z=9]
(4x + 7y = 46, y + z = 9)
7y = 46 - 4x = 7(9 - z)
X = (1, 6, 3) + λ (7, -4, 4)