Diferencia entre revisiones de «Tutorial:Tramando Cuadriláteros»

m (title) |
m (link) |
||
| Línea 37: | Línea 37: | ||
* ''¿Cómo harían para encontrar un par de posiciones de '''I''' que hagan que cada correspondiente "inscripto" resulte semejante al otro?'' o | * ''¿Cómo harían para encontrar un par de posiciones de '''I''' que hagan que cada correspondiente "inscripto" resulte semejante al otro?'' o | ||
* ''¿Cómo creen que podría lograrse que la ''familia'' de todos los ''inscriptos'' que se logren al desplazar '''I''' resulten rectángulos, rombos o trapecios?''. | * ''¿Cómo creen que podría lograrse que la ''familia'' de todos los ''inscriptos'' que se logren al desplazar '''I''' resulten rectángulos, rombos o trapecios?''. | ||
| − | Algunas de las maniobras podría llevar a algún logro, al menos según se lo pudiera apreciar a simple vista y, en tal caso, sería importante cuestionarse sobre cómo controlar con mayor rigor, acudiendo a la [[File:Tool Relation between Two Objects.gif]] [[Herramienta de Relación]] y/o a la información complementaria que ofrece la [[Vista Algebraica]]. | + | Algunas de las maniobras podría llevar a algún logro, al menos según se lo pudiera apreciar a simple vista y, en tal caso, sería importante cuestionarse sobre cómo controlar con mayor rigor, acudiendo a la [[File:Tool Relation between Two Objects.gif]] [[Herramienta de Relación]] y/o a la información complementaria que ofrece la [[Comentarios:Vista_Algebraica_CAS|Vista Algebraica]]. |
; | ; | ||
En cada ocasión, valdría analizar las condiciones que se procuraron para cada logro para poder reproducirlo sin necesidad de volver a tanteos que, en todo caso, se facilitan poniendo a la Vista la Cuadrícula y activando la alternativa ''Ajusta a Cuadrícula'' desde la opción de la [[Vista Gráfica#Barra de Estilo|Barra de Estilo]]. | En cada ocasión, valdría analizar las condiciones que se procuraron para cada logro para poder reproducirlo sin necesidad de volver a tanteos que, en todo caso, se facilitan poniendo a la Vista la Cuadrícula y activando la alternativa ''Ajusta a Cuadrícula'' desde la opción de la [[Vista Gráfica#Barra de Estilo|Barra de Estilo]]. | ||
Revisión del 07:09 31 mar 2020
A lo largo de esta propuesta, conviene ir produciendo, paso a paso, la construcción del planteo en la Ventana de GeoGebra.
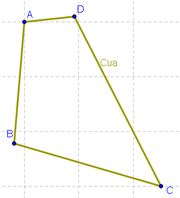
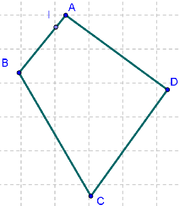
Cuadrilátero de Partida
1 Empleando la ![]() Herramienta de Polígono, construimos un cuadrilátero cualquiera con vértices en los puntos A, B, C y D respectivamente (recordando volver a dar clic sobre el punto inicial A para "cerrar" el polígono). Para su mejor identificación, se activa el Menú Contextual, apelando a la alternativa desde la que se lo Renombra cua.
Herramienta de Polígono, construimos un cuadrilátero cualquiera con vértices en los puntos A, B, C y D respectivamente (recordando volver a dar clic sobre el punto inicial A para "cerrar" el polígono). Para su mejor identificación, se activa el Menú Contextual, apelando a la alternativa desde la que se lo Renombra cua.
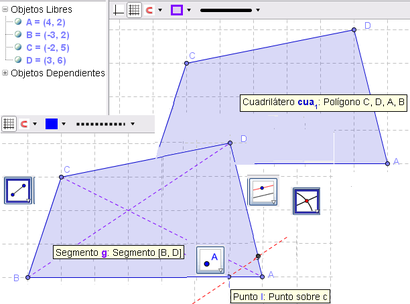
2 Con la Herramienta de Punto, creamos uno, I, sobre el segmento de lado que une los puntos A y B.
3 Se trazan las diagonales de cua con la ![]() Herramienta de Segmento.
Herramienta de Segmento.
Como los puntos vértices de cua son libres, se los puede desplazar hasta quedar conformes con el cuadrilátero resultante.
4 Desde el punto creado sobre el lado entre A y B, se traza una ![]() paralela a la diagonal entre A y C y otra a la que une B y D.
paralela a la diagonal entre A y C y otra a la que une B y D.
5 Con la ![]() herramienta correspondiente, se establecen los puntos de intersección entre cada paralela y los lados que unen A con D y B con C respectivamente.
herramienta correspondiente, se establecen los puntos de intersección entre cada paralela y los lados que unen A con D y B con C respectivamente.
6 Por uno de los recientes puntos de intersección creados - el que está sobre el lado que une A con D-, se traza la ![]() paralela a diagonal entre A y C y se establece su
paralela a diagonal entre A y C y se establece su ![]() punto de intersección con el lado que conecta D con 'C'.
punto de intersección con el lado que conecta D con 'C'.
Cuadrilátero Inscripto
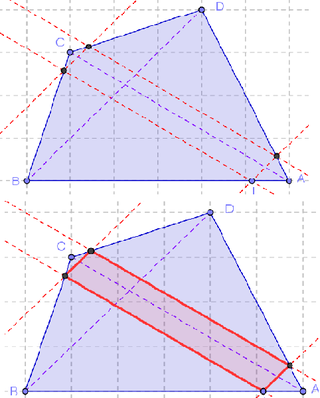
De este modo se completa el trazado de los cuatro puntos en cada lado...
7 Volvemos a apelar a la Herramienta de Polígono para crear el que une cada uno de los puntos recién creados sobre cada lado.
Desplazamientos Libres
8 Es sencillo notar que todos los vértices del cuadrilátero A, B, C, D son libres y que al desplazarlos se modifica el tipo de cuadrilátero que acabamos de "inscribir" en cua (el de ABCD) y que de entre los del inscripto, solo I puede moverse a lo largo del lado de A a B de cua.
Registros de Ensayos
9 Para explorar con un propósito guía que conduzca las observaciones, podemos plantearnos y/o plantearles a los estudiantes, una serie de desafíos. Por ejemplo...
- ¿Cómo harían para encontrar un par de posiciones de I que hagan que cada correspondiente "inscripto" resulte semejante al otro? o
- ¿Cómo creen que podría lograrse que la familia de todos los inscriptos que se logren al desplazar I resulten rectángulos, rombos o trapecios?.
Algunas de las maniobras podría llevar a algún logro, al menos según se lo pudiera apreciar a simple vista y, en tal caso, sería importante cuestionarse sobre cómo controlar con mayor rigor, acudiendo a la ![]() Herramienta de Relación y/o a la información complementaria que ofrece la Vista Algebraica.
Herramienta de Relación y/o a la información complementaria que ofrece la Vista Algebraica.
En cada ocasión, valdría analizar las condiciones que se procuraron para cada logro para poder reproducirlo sin necesidad de volver a tanteos que, en todo caso, se facilitan poniendo a la Vista la Cuadrícula y activando la alternativa Ajusta a Cuadrícula desde la opción de la Barra de Estilo.
Exploraciones con Metas y Controles
10 Los interrogantes que en el camino de las exploraciones pueden reiterarse apuntan a...
- ¿Cómo controlar que se llega a cada una de las metas propuestas? y
- ¿Qué herramientas conviene emplear y qué relaciones verificar?
- El método que se emplee para lograr cada uno de los cuadriláteros de distinto tipo, ¿será el único?
- ¿Será válido en todos los casos?
- ¿Cómo podríamos asegurarlo?
- ¿Habrá algunas metas imposibles de lograr?
- ¿Cómo podríamos convencernos de esta eventual imposibilidad?
Convicciones y Argumentaciones
En el camino de ensayos, controles y debates, posiblemente surja la convicción respecto del tipo de cuadrilátero que resulta el inscripto.
Máxime cuando no se logra un trapecio propiamente dicho sino, paralelogramos en todos los ensayos.
Llegada esta instancia, es conveniente abrir un espacio de argumentaciones que procuren justificar este fenómeno.