Diferencia entre revisiones de «Comando Trilineal»

De GeoGebra Manual
m |
m (Texto reemplazado: «;([a-zA-Z0-9]*)\[(.*)\]» por «;$1($2)») |
||
| Línea 2: | Línea 2: | ||
{{revisar}} | {{revisar}} | ||
| − | ;Trilinear | + | ;Trilinear( <Punto>, <Punto>, <Punto>, <Número>, <Número>, <Número> ):Crea un punto de [[w:Trilinear coordinates|coordenadas trilineales]] correspondientes a la terna de números dados, respecto de un triángulos cuyos vértices son los puntos indicados.<br>Así: '''<code>Trilinear[A, B, C, u, v , w]</code>]''' crea el punto de [[w:Trilinear coordinates|coordenadas trilineales]] ''''u, v, w''''' (terna de números dados) relativas al triángulo '''<code>ABC</code>''' (sus vértices son los tres puntos indicados). |
:{{Example|1='''<code>Trilineal[A, B, C, u, v, w]</code>''' crea un punto cuyas [[w:Trilinear coordinates|coordenadas trilineales]] respecto del triángulo '''<code>ABC</code>''' son ''(u, v, w)''.}}<small><center> | :{{Example|1='''<code>Trilineal[A, B, C, u, v, w]</code>''' crea un punto cuyas [[w:Trilinear coordinates|coordenadas trilineales]] respecto del triángulo '''<code>ABC</code>''' son ''(u, v, w)''.}}<small><center> | ||
:{{Note|1=Las distancias de ese punto a los lados ''a'', ''b'' y ''c'' del triángulo '''<code>ABC</code>''' serán '''<code>(|ku|,|kv|,|kw|)</code>''' siendo<br><big>k = <math>\frac{2 Area(ABC)}{au+bv+cw}</math></big> }}</center></small> | :{{Note|1=Las distancias de ese punto a los lados ''a'', ''b'' y ''c'' del triángulo '''<code>ABC</code>''' serán '''<code>(|ku|,|kv|,|kw|)</code>''' siendo<br><big>k = <math>\frac{2 Area(ABC)}{au+bv+cw}</math></big> }}</center></small> | ||
Revisión del 20:04 8 oct 2017
Trilineal
Categorías de Comandos (todos)
| Página en proceso de traducción. |
- Trilinear( <Punto>, <Punto>, <Punto>, <Número>, <Número>, <Número> )
- Crea un punto de coordenadas trilineales correspondientes a la terna de números dados, respecto de un triángulos cuyos vértices son los puntos indicados.
Así:Trilinear[A, B, C, u, v , w]] crea el punto de coordenadas trilineales 'u, v, w (terna de números dados) relativas al triánguloABC(sus vértices son los tres puntos indicados). - Ejemplo:
Trilineal[A, B, C, u, v, w]crea un punto cuyas coordenadas trilineales respecto del triánguloABCson (u, v, w). - Nota: Las distancias de ese punto a los lados a, b y c del triángulo
ABCserán(|ku|,|kv|,|kw|)siendo
k = \frac{2 Area(ABC)}{au+bv+cw}
Algunos Ejemplos
| Punto | u | v | w |
|---|---|---|---|
| A | 1 | 0 | 0 |
| B | 0 | 1 | 0 |
| C | 0 | 0 | 1 |
| Centrocircuncentro circunferencia circunscripta | cos(\hat{A}) | cos(\hat{B}) | cos(\hat{C}) |
| Centro circunferencia inscriptaIncentro | 1 | 1 | 1 |
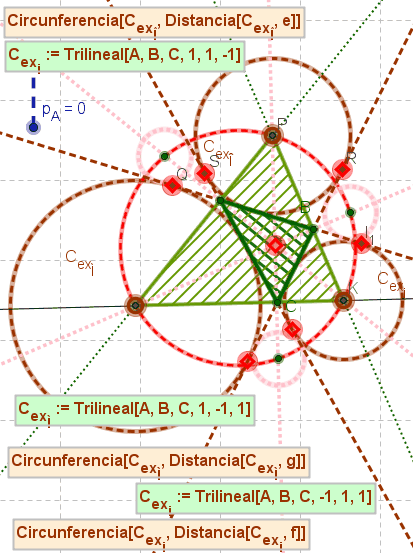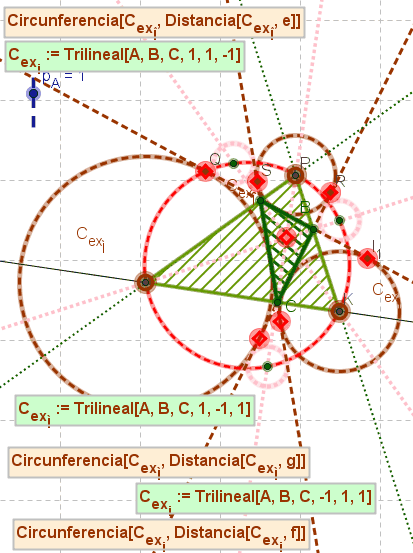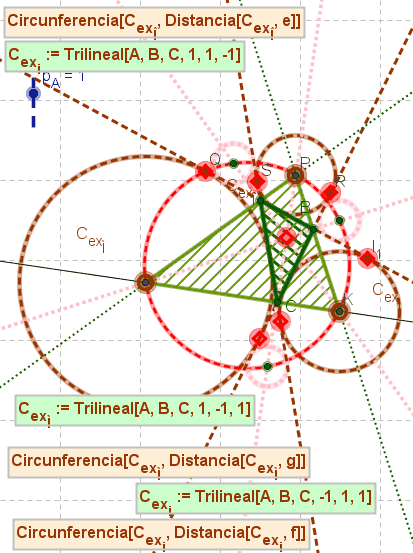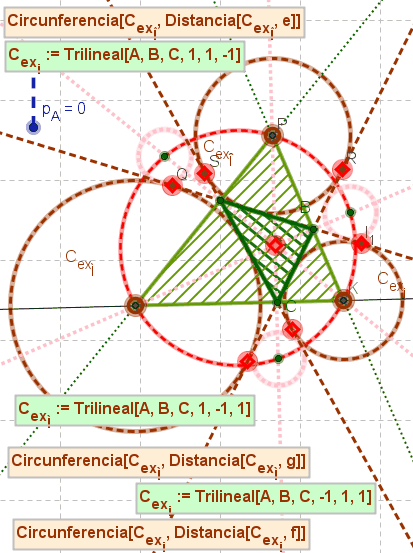
| Centro ex-inscripta tangente a [BC] | -1 | 1 | 1 |
| Centro ex-inscripta tangente a [AC] | 1 | -1 | 1 |
| Centro ex-inscripta tangente a [AB] | 1 | 1 | -1 |
| Centro de gravedad | \frac{1}{a} | \frac{1}{b} | \frac{1}{c} |
| Ortocentro | cos(\hat{B}) cos(\hat{C}) | cos(\hat{A}) cos(\hat{C}) | cos(\hat{A})cos(\hat{B}) |
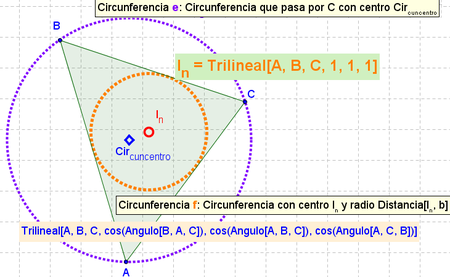
- Ejemplos: La figura ilustra modos de obtener puntos como...
Incentro = Trilineal[A, B, C, 1, 1, 1]desde el que se puede trazar laCircunferencia[Cir_{cuncentro}, Distancia[I_n, b]]Circuncentro = Trilineal[A, B, C, cos(Angulo[B, A, C]), cos(Angulo[A, B, C]), cos(Angulo[A, C, B])]desde el que se puede trazar laCircunferencia[Cir_{cuncentro}, C]
- Nota: Ver también los comandos Cúbica, CentroTriángulo y CurvaTriangular.