Comando PolígonoFrecuencias

| Página en proceso de traducción. |
PolígonoFrecuencias
Categorías de Comandos (todos)
- Nota: El comando traza la poligonal que une cada punto medio del segmento superior de las barras de un histograma por lo que produce un efecto análogo al del comando Histograma.
- PolígonoFrecuencias[ <Lista de Límites de Clase>, <Lista de Alturas> ]
- Crea un Polígono de Frecuencias con vértices en las barras correspondientes. Los extremos del intervalo de clase determinan el ancho y la posición de cada barra. Los límites de clase determinan, así, sus abscisas y las alturas, las ordenadas en el correspondiente histograma cuyas marcas de clase van a unirse para trazar el polígono.
- Ejemplo:
PolígonoFrecuencias[{0, 1, 2, 3, 4, 5}, {2, 6, 8, 3, 1}]crea un Polígono de Frecuencias que une con segmentos las marcas de clase de las 5 barras de las alturas especificadas para el correspondiente histograma. La primera barra estaría ubicada en el intervalo [0, 1] con marca de clase 2, la segunda, en el intervalo [1, 2] con marca de clase 6 y así sucesivamente. - Nota: Por otros ejemplos, ver el comando Histograma.
- PolígonoFrecuencias[ <Lista de Límites de Clase>, <Lista de Datos Brutos>, <Uso de Densidad (true/false)> , <Factor de Escala de Densidad> (opcional) ]
- Crea un Polígono de Frecuencias en que la lista de límites de clase determinan las abscisas de los vértices y las ordenadas, se vinculan a la lista de datos en bruto del siguiente modo:
- Si el parámetro booleano es cierto, será la altura = (Factor de Escala de Densidad) * (frecuencia de clase) / (ancho de clase)
- Si es falso, será la altura = frecuencia de clase
- Por omisión, la densidad es verdadera y el factor de escala, 1.
Los extremos del intervalo de clase determinarían, en el histograma correspondiente, el ancho y la posición de cada barra, así como cuántos elementos de los datos corresponderán a cada clase y, desde ya. las marcas a unir con los segmentos de la poligonal establecida.
- Ejemplo:
PolígonoFrecuencias[{1, 2, 3, 4}, {1.0, 1.1, 1.1, 1.2, 1.7, 2.2, 2.5, 4.0}]crea el polígono de frecuencias correspondiente a un histograma de 3 barras, cada una de las cuales tendrá las siguientes alturas y marcas de clase: 5 (primera barra), 2 (segunda barra) y 1 respectivamente. - PolígonoFrecuencias[ <Acumulada o no (true/false)> , <Lista de Límites de Clase>, <Lista de Datos Brutos>, <Uso de Densidad (true/false)> , <Factor de Escala de Densidad> (opcional) ]
- Si la Acumulada es verdadera se crea un Polígono de Frecuencias sobre la lista de límites de clase, de la lista de datos en bruto. Los extremos del intervalo de clase determinarían Polígono de Frecuencias sobre la lista de límites de clase, de la lista de datos en bruto. Los extremos del intervalo de clase determinarían, en el histograma correspondiente, el ancho y la posición de cada barra, así como cuántos elementos de los datos corresponderán a cada clase y, desde ya. las marcas a unir con los segmentos de la poligonal establecida.
- Si el parámetro booleano es verdadero, se crea un polígono de frecuencias donde cada vértice tiene una ordenada igual a la frecuencia de la clase más la suma de todas las previas.
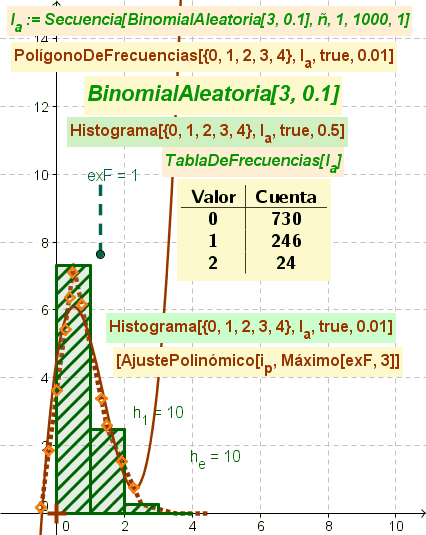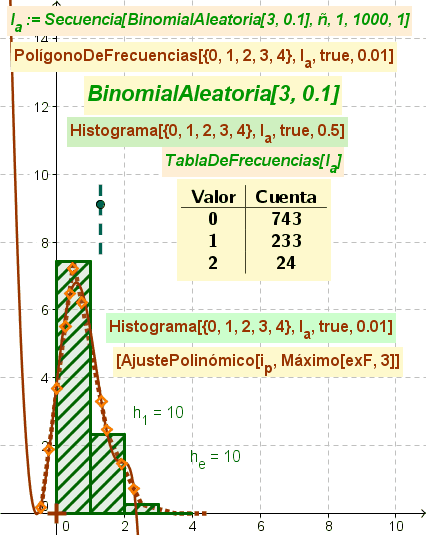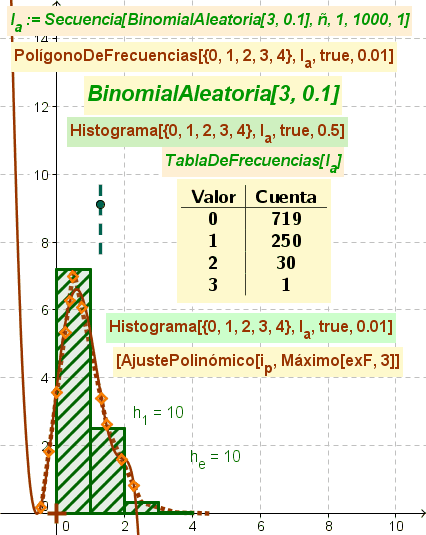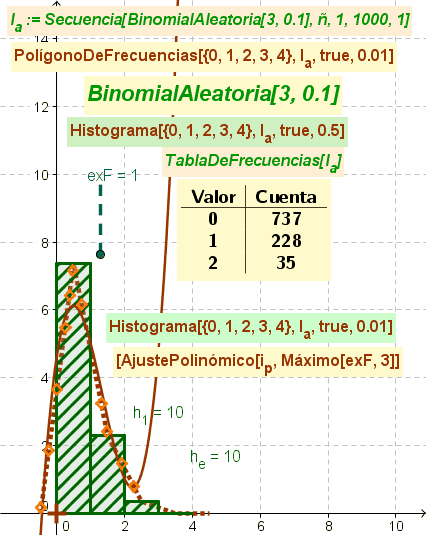
En la figura se ilustra animadamente la producción de una lista de datos en bruto que permite elaborar una Tabla de Frecuencias y un adecuado Polígono de Frecuencias, además del Histograma previo. Se suma un AjustePolinómico con grado acorde al valor del deslizador (3 como mínimo) respecto de puntos aleatoriamente distribuidos sobre el Polígono de Frecuencias creado para completar el estudio del tema.
De hecho, se exponen dos histogramas que contienen la misma información y únicamente se diferencian por el factor de escala dado que solo en el que tiene un valor decimal adecuado permite apreciar claramente la última clase (cuando, eventualmente, se produce).
La producción de valores que incluyan esa última clase tiene escasa probabilidad en tanto deriva de una secuencia en que los datos se producen según una BinomialAleatorio[3, 0.1]




