Diferencia entre revisiones de «Tutorial:Triángulos de Todo Tipo»

m (link) |
m (link) |
||
| Línea 30: | Línea 30: | ||
'''[[File:Preparativos_Tri_0_5.PNG |250px|thumb|center]]''' | '''[[File:Preparativos_Tri_0_5.PNG |250px|thumb|center]]''' | ||
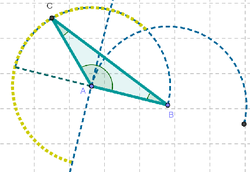
| − | {{step|num=10}}Usando la [[Comentarios: | + | {{step|num=10}}Usando la [[Comentarios:Herramienta_de_Refleja_Objeto_por_Punto|Herramienta de Punto]] trazamos, uno en el segmento que une el centro de la primera semicircunferencia y su extremo izquierdo; otro, sobre la primera semicircunferencia y el tercero, en el arco recientemente trazado.. |
'''[[File:Preparativos_Finales_para_Tri.png |250px|thumb|center]]''' | '''[[File:Preparativos_Finales_para_Tri.png |250px|thumb|center]]''' | ||
Revisión del 23:11 26 mar 2020
¿Cómo construir triángulos de todo tipo en cualquier dispositivo?
Para seguir la tutela de este instructivo de Centro Babbage, conviene abrir la pantalla de Ventana GeoGebra y avanzar paso a paso. En este instructivo, se intentará construir triángulos dinámicos de distinto tipo, empleando las herramientas que ofrece GeoGebra.
La idea es emplear lo menos posible los puntos fijados por las intersecciones sino apelar a los recorridos que dinámicamente lleven a establecer triángulos dinámicos de diverso tipo.
Mientras se construye este triángulo dinámico, se aprenderá cómo emplear una serie de herramientas.
1 En el Menú Vista, destildamos Ejes y controlamos que esté tildado Cuadrícula.
2 Seleccionamos la Herramienta de Semicircunferencia y damos clic en dos posiciones de la Vista Gráfica, una más a la izquierda que la otra, para que quede trazada esta semicircunferencia.
3 Seleccionamos la Herramienta de Medio o Centro, seleccionando los dos puntos extremos de la semicircunferencia recién trazada. Al quedar trazado este .tercer punto, empleamos la Herramienta de Segmento para trazar el que une este tercer punto con el del extremo izquierdo de la semicircunferencia.
4 Seleccionamos la Herramienta de Perpendicular para trazar la que pasa por el punto medio y resulte perpendicular al segmento recién trazado.
5 Pasamos a la Herramienta de Simetría Central para reflejar el punto medio entre los extremos de la semicircunferencia a través del punto del extremo derecho de la semicircunferencia.
6 Empleamos nuevamente la Herramienta de Semicircunferencia para trazar otra semicircunferencia que tenga por extremos el punto medio entre los extremos de la anterior y el punto recientemente reflejado.
7 Seleccionamos la herramienta que interseca dos objetos para encontrar el punto en que se intersecan la perpendicular recién trazada con la semicircunferencia que atraviesa y aquel en que se cruzan ambas semicircunferencias.
8 Pasamos a seleccionar nuevamente la Herramienta de Simetría Central para reflejar el punto en que se interseca la perpendicular trazada con la semicircunferencia por el punto medio entre los extremos de esta semicircunferencia.
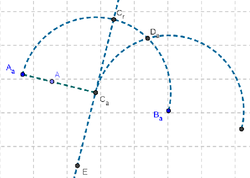
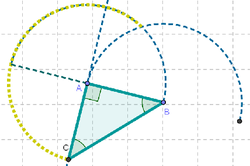
9 Con la Herramienta de Arco de Circunferencia, trazamos el arco que tiene centro en el punto medio entre los extremos de la primera semicircunferencia y extremos en el punto de intersección de ambas semicircunferencias y el reflejado reciente (de la intersección de la perpendicular y la primera semicircunferencia por el c punto central de esta semicircunferencia).
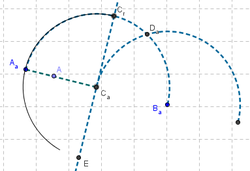
10 Usando la Herramienta de Punto trazamos, uno en el segmento que une el centro de la primera semicircunferencia y su extremo izquierdo; otro, sobre la primera semicircunferencia y el tercero, en el arco recientemente trazado..
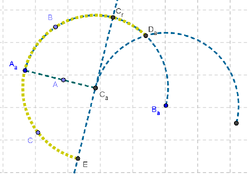
11 Con la Herramienta de Polígono unimos estos tres puntos recientemente creados para obtener un triángulo tal que, cuando...
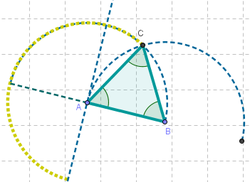
- uno de los vértices (el que se desplaza por el segmento) ocupa el punto central de la primera semicircunferencia
- el segundo se ubica en el extremo derecho de la semicircunferencia y
- el tercero en el punto de intersección de ambas semicircunferencias...
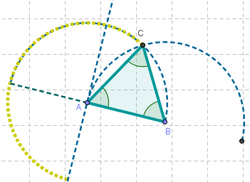
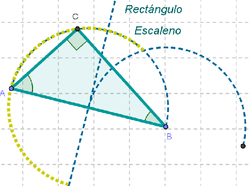
... se obtiene un equilátero.
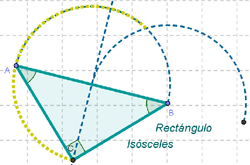
12 Si se desplaza el último de los vértices, se obtienen una variedad de triángulos isósceles de los cuales es, además, rectángulo el del extremo del arco que recorre.
¿Qué se observa cuando se lleva...
- el primer vértice del centro al extremo izquierdo de la primera semicircunferencia,
- el segundo en el otro extremo y
- el último se desplaza por el arco trazado?
13 En cada oportunidad se puede verificar la longitud de los lados del triángulo trazado y compararlos empleando la Herramienta de Relación para verificar cuándo son iguales de dos en dos, los tres lados.
14 Si aplicamos la Herramienta de Ángulo sobre el triángulo trazado, podemos controlar en qué momento uno de los ángulos resulta recto.
15 Es conveniente seleccionar en el Menú Contextual las Propiedades de Objeto para darle estilo punteado a cada uno de los trazos auxiliares de esta construcción .
16 Controlar cuándo y cómo el triángulo resulta isósceles rectángulo, cuándo equilátero y cuando es un isósceles de distinto tipo.
Aplicaciones para Tablets
Para realizar construcciones en Tablets, conviene seguir las indicaciones que se detallan a continuación y/o las anotadas en el siguiente artículo.
| También pueden apreciarse videos como este y consultar la Guía de Referencia Rápida para Aplicaciones en Tablets. |
Instalación
Se puede descargar en dispositivos Android en los que corre Android 4.0.3 o superior con pantallas de 7 y iPad 2 en adelante. Tal aplicación app cuenta con tres modos.
- Para instalar en Amazon Kindle, basta con dirigirse en el sitio de despacho de Amazon (Amazon store) a GeoGebra o proceder a un clic oportuno. Resultaría eficaz con todos los dispositivos Kindle Fire salvo los de primera generación.
- Para instalar toda aplicación app en cualquier otro dispositivo Android, debiera tomárselo del despacho Opera Mobile Store
Modo de Edición
Las aplicaciones app debieran empezar en este modo con la vista correspondiente mostrando una construcción vacía.
Se pueden emplear las herramientas de la Barra en la zona inferior de la pantalla, descriptas a continuación, para crear los nuevos objetos.
Barra de Menús
En la franja superior de la pantalla, se puede ver una Barra de Menús con diversos íconos:
 Nuevo/New para crear un nuevo archivo
Nuevo/New para crear un nuevo archivo Llaves de Búsqueda/Search para agilizar el modo de búsqueda sea para encontrar las construcciones guardadas localmente o en GeoGebra
Llaves de Búsqueda/Search para agilizar el modo de búsqueda sea para encontrar las construcciones guardadas localmente o en GeoGebra Guarda/Save guarda la construcción que se estuviera desarrollando con el título que se puede escribir a la derecha de ese botón.
Guarda/Save guarda la construcción que se estuviera desarrollando con el título que se puede escribir a la derecha de ese botón.
Al modificar el título de la construcción también se procede a guardarla. El botón para guardar pasa estar inactivo cuando todos los cambios ya se hubieran almacenado. Deshace/Undo, Rehace/Redo para deshacer o reiterar un paso de construcción
Deshace/Undo, Rehace/Redo para deshacer o reiterar un paso de construcción
Creando Objetos
Se pueden emplear las herramientas de la Barra en la zona inferior de la pantalla, ya descriptas, para crear los nuevos objetos.
Los íconos y las mismas posibilidades básicas de as herramientas disponibles para operar en la tablet coinciden con las correspondientes de la versión usual para equipos no móviles.
Alternancia de Herramientas
En la zona superior de cada episodio se puede saber, tal como en el escritorio de aplicaciones de GeoGebra, que es posible alternar ("swiping") algunas herramientas. Para dibujar un segmento, con la Herramienta de Segmento se debe apuntar con el dedo el punto de inicio y deslizarlo hasta el extremo final.
Este mismo mecanismo es el adecuado para semirrectas o rectas.
Comandando
En el extremo inferior derecho, aparece una diminuta Barra de entrada en la que se puede activar con un clic, una amplia Barra de Entrada emergente permite el uso de los comandos de GeoGebra o anotar funciones y ecuaciones.
- Para activar el rastro de un punto A ya creado, se puede emplear
Rastro(A, true) - Para activar la animación de un deslizador ya creado t, se puede emplear
IniciaAnimación(t) - Para cambiar la razón o proporción entre los ejes EjeX:EjeY basta emplear el comando
RazónEjes(1, 2) - Para cambiar el estilo del punto A para que aparezca tal otro 'X', basta con establecerlo como use
EstiloPunto(A, 1)
- Para activar el rastro de un punto A ya creado, se puede emplear
Modo Buscador
En este modo se puede abrir las construcciones guardadas localmente (sector izquierdo de la pantalla) o tomadas de GeoGebra (sección derecha).
El primer clic selecciona la construcción y expone las opciones:
- Abrir en modo Hoja de Trabajo
- Abrir en modo de Edición
- Borrar la construcción
Un segundo clic en la construcción opera como si se abriera en modo Hoja de Trabajo (Worksheet).
Modo de Hoja de Trabajo
En este modo se pueden ver hojas de trabajo GeoGebra incluyendo las de instrucciones por encima y debajo de la construcción. Las hojas locales se exponen sin instrucciones.