Tutorial:Preparando Herramientas Propias en la Barra

Tutorial: Reconstruir un triángulo perdido dados sus puntos de rastro Diseño del Centro Babbage

Lista de Tutoriales

Instrumentarse gracias al Teorema de Pitágoras

El desafío es encontrar el modo de controlar si el mecanismo empleado para obtener un cuadrado equivalente - de igual área - a un rectángulo ofrecido es eficaz en todos los casos. Esto requiere una justificación argumental según las reglas de juego del quehacer matemático.

Preparativos

En el Menú Apariencias, es preciso seleccionar la adecuada, por ejemplo, Algebra y Gráficos y:

• dejar activa la Barra de Estilo
• ocultar los ejes de coordenadas.
• en el Menú de Opciones, establecer un Rotulado, Sólo para los Nuevos Puntos
• en el Menú Vista, seleccionar la Hoja de Cálculo.

Pasos de Construcción

El recorte del Protocolo de Contrucción que aparece a continuación, registra los pasos para plantear el escenario de trabajo.

La secuencia de pasos culmina con los retoques y ajustes para que el escenario dinámico resulte ilustrativo.

Analizando el Mecanismo

En el escenario planteado, los puntos:

• A y B permiten, al desplazarse, determinar la mayor o menor longitud de la base del rectángulo y
• el que se denomina C_1 - representado por un rombo hueco en el dibujo -, establece la altura que tendrá, como fracción de la base.

Es conveniente rehacer el escenario delante de los destinatarios y centrar el desafío en el análisis del mecanismo. explorando y controlando resultados.

Sumando Registros: La Hoja de Cálculo

La Hoja de Cálculo puede contener en cada celda, los valores que ponen algebraicamente en evidencia el quid de la eficacia general. Así, se pueden ubicar los distintos valores en cada celda:

• en la primera fila, se disponen los valores de:
  • a, b, a b así como l_x^2 (la media armónica entre a y b) y
  • la expresión que explica las relaciones en juego - (x² + a²) + (x² + b²) = (a + b)² - que dará un resultado apenas se la ingrese.

Archivo:Pitagoras Vaya.PNG

Para analizar la expresión, se debe tener en cuenta que:

• cada una de las sumas entre paréntesis en el primer miembro, se corresponden con el cuadrado de uno y otro cateto del triángulo naranja - dado que x es su altura a la hipotenusa y a y b, la base y altura del rectángulo respectivamente -
• el segundo miembro presenta el cuadrado de la hipotenusa del triángulo naranja compueda por a y b.

El valor que aparecerá en la celda en que se vuelca esta expresión será justamente el de la media armònica mencionada, que da lado al cuadrado equivalente al rectángulo de área a b.

Creating Custom Tools

GeoGebra allows you to create custom tools. This means that you can extend the toolbar by creating your own tools. Let’s now create a tool that determines the minimal distance between a line and a point (e.g. altitude in a triangle). Before you can create your custom tool you need to construct all the objects required for your tool.

Prepare the construction

Preparations

• Open a new GeoGebra window.
• Switch to Perspectives – Geometry.
• Change the labeling setting to All New Objects (menu Options – Labeling).

Construction Steps

1		Create line a through two points A and B.
2		Insert a new point C.
3		Create perpendicular line b to line a through point C.
4		Construct intersection point D of lines a and b.
5		Create segment c between points C and D.
6		Drag points A, B and C to check your construction.
7		Change the color of segment c and hide the labels of all objects.

Create a custom tool

1. In menu Tools click on Create New Tool… to open the Create New Tool dialog window.

2. By default, tab Output Objects is activated.

3. Specify the output objects of your new tool by either clicking on the desired output object on the drawing pad (our example: segment c) or selecting it from the drop down menu (click on the little arrow next to the input field).

4. Click the Next > button in order to activate tab Input Objects.

5. GeoGebra fills in the corresponding input objects for your tool automatically (our example: points A, B and C). {{note||GeoGebra picks all so-called parent objects of the output objects you specified.

6. Click the Next > button in order to activate tab Name & Icon.

7. Fill in a name for your tool and text for the toolbar help.

Nota: GeoGebra fills in the text field Command name automatically.

8. Click the button Finish.

Aviso: Your new tool is now part of the GeoGebra toolbar.

Try out your custom tool

1. Open a new GeoGeba window using menu File – New.

Nota: Your custom tool is still part of the tool bar.

2. Create a triangle ABC using tool Polygon.

3. Activate your custom tool Altitude.

4. Click on points A, B and C in order to create one of the triangle’s altitudes.

5. Create another altitude of the triangle.

6. Intersect the two altitudes to get the orthocenter of the triangle.

Saving and Importing Custom Tools

Save your custom tool

1. In menu Tools click on Manage tools… to open the Manage tools dialog window.

2. Select your custom tool Altitude from the list of available tools.

3. Click on button Save as… in order to save your custom tool and make it available for future constructions.

4. Choose a name for your custom tool (e.g. Altitude_tool.ggt) and save it on your computer.

Custom GeoGebra tools are saved with the file name extension .ggt. This helps you to distinguish between usual GeoGebra files (extension .ggb) and custom tool files.

Import a custom tool

After saving your custom tool you are able to reuse it in future constructions. By default the GeoGebra tool bar doesn’t include any custom tools. In order to reuse one of your custom tools you need to import it into your new GeoGebra window.

1. Open a new GeoGebra window.

2. In menu File click on Open.

3. Look for the custom tool you saved earlier (e.g. Altitude_tool.ggt) and select it from the list of available GeoGebra files (.ggb) and tool files (.ggt).

4. Click the Open button to import your custom tool into the toolbar of the new GeoGebra window.

Aviso: Importing a custom tool doesn’t affect the construction in your GeoGebra window. Thus, you can also import custom tools during a construction process.

Tutorial: Diagonal de un Cuadrado Basado en un Diseño de un Taller del Centro Babbage

Lista de Tutoriales

Planteo

Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del Polígono Regular?

En este tutorial, se compara el cuadrado que puede crearse con la Polígono Regular con el de una Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.

1 Seleccionar una adecuada del Menú Apariencias y activar la Barra de Estilo en la Vista Gráfica para completar los preparativos.

Preparativos

Ocultar los ejes coordenados, exponer la cuadrícula y optar por la alternativa con la que se Ajusta a Cuadrícula' en la Barra de Estilo.

Paso a Paso

2 Marcar dos puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..

3 Trazar...

• el punto medio y la mediatriz entre estos puntos
• la circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
• los puntos de intersección entre la mediatriz y la circunferencia
• la semicricunferencia que se extiende entre uno y otro punto de intersección
• un punto sobre esta semicircunferencia
• el punto que refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia
• las rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente.

4 Construir el polígono que tiene como vértices:

• el punto sobre la semicircunferencia,
• uno de los extremos de la diagonal del cuadrado en marcha,
• el punto reflejado,
• el otro extremo de la diagonal

5 Desplazar el punto que se trazó sobre la semicircunferencia hasta que ocupe la posición en que parece un cuadrado.

Justificaciones y Controles

El boceto se traza de modo tal que el punto que se desplaza sobre la semicircunferencia, su reflejado y los contiguos - vértices de la diagonal - conformen...

• un rectángulo
  • que deviene cuadrado cuando se lo lleva hasta uno de los de intersección - ambos son extremos del recorrido por el que hasta se lo podría animar.

Conviene controlar...

• de modo más certero este comportamiento, empleando las herramientas adecuadas para contar con información sobre valores y relaciones
• las argumentaciones respecto a las vinculaciones entre el resultado de los ensayos y lo que la construcción desencadena en todos los casos.

Un Quehacer a Proyectar y Compartir

Pese a que lo más evidente - desde la óptica docente - es que la primera de las actividades depende directamente del empleo de herramientas con las que es preciso familiarizarse, ambas se entrecruzan con operaciones sobre la construcción dinámica:

• en exploraciones - guiadas por un propósito - que van dando entidad a...
  • justificaciones causales de los efectos de ciertas maniobras - ¿es rectángulo? - ¿siempre? - ¿cómo hacemos para asegurarlo? - ¿cuándo parece pasar a cuadrado? - ....
  • las relaciones entre los elementos que es preciso develar para respaldar la cadena de causalidades
  • las correlaciones entre efectos, trazado y propiedades en juego que requieren un estudio conceptual
• ... de hecho, es la necesidad de validar estas presunciones lo que da razón de ser a su estudio.

Este recorrido expone un modelo de quehacer matemático que, escasamente transitado en términos generales frente a los estudiantes y con ellos, permite proyectarlo como medio de formación que puede completarse en intercambios virtuales.

Herramientas para el Control de Ensayos y Presunciones

6 Emplear las herramientas necesarias para controlar qué tipo de cuadrilátero se ha construido. Por ejemplo:

• la que traza y mide sus ángulos para corroborar que, tal como parece, son rectos
• la que mide la longitud de cada lado
• la que informa sobre la relación entre los segmentos de los lados y de las correspondientes rectas.

7 Procurar descripciones argumentadas sobre el tipo de cuadrilátero que se establece a medida que se desplaza el punto sobre la semicricunferencia.

Herramientas Propias para Completar las Disponibles

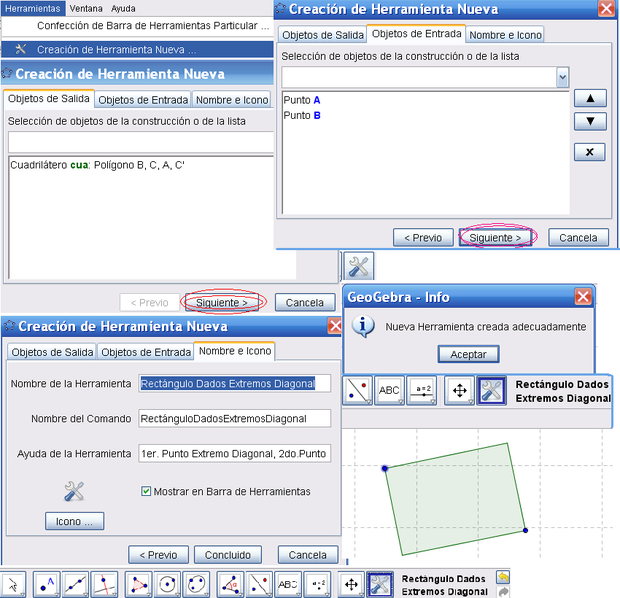
8 - Opción más Avanzada Dirigirse al manual para conocer la serie de pasos a partir de los cuáles, seleccionando el cuadrilátero creado como objeto de salida en la Caja de Diálogo de Creación de Herramientas de la opción Creación de Herramienta Nueva del Menú de Herramientas, se puede crear la propia.

• En este caso, la que traza rectángulos (que pueden establecerse como cuadrados), dada su diagonal, como ilustra la siguiente figura.

• Habría que incluirlos en el listado correspondiente, si además del cuadrilátero (polígono), se deseara que otros elementos se expusieran en la salida (como los puntos vértices adicionales a los dados, los segmentos de lado, las rectas que los contienen, la semicircunferencia por la que se desplaza uno de los puntos de entrada, etc.).
• Una vez creada la herramienta, es posible cambiar el ícono que la acompaña así como otros detalles - nombre, ayuda -.

Tutorial: Diagonal de un Cuadrado Basado en Diseño de un Taller de Centro Babbage

Lista de Tutoriales

The Fibonacci Spiral

A Fibonacci spiral can be created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling which uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21,… The Fibonacci spiral approximates the so called Golden Spiral which is a logarithmic spiral whose growth factor is related to the golden ratio.

Preparations

• Open a new GeoGebra window.
• Import your Square tool into the toolbar (menu File – Open).
• Switch to Perspectives – Geometry.
• Change the labeling setting to No New Objects (menu Options – Labeling).

Construction Steps

1		Use your Square tool to create a square with side length 1. Aviso: Place the two points on grid points that are next to each other.
2		Create a second square with side length 1 below the first square. Aviso: Use already existing points to connect both squares.
3		Create a third square with side length 2 on the right hand side of the two smaller squares.
4		Continue creating squares with side lengths 3, 5, 8 and 13 in counter clockwise direction.
5		Create a circular arc within the first square you created. Aviso: Specify the lower right vertex of the square as the center of the arc. Select two opposite vertices of the square in counter clockwise orientation.
6		Repeat step 5 for each of the squares in order to construct the Fibonacci spiral.
7		Enhance your construction using the Properties dialog.

Constructing the Center of a Circle

Back to school…

Do you know how to construct the center of a circle? Use the circles provided by your workshop presenter (4 per participant) and try to find a way of finding the center of these circles (a) only by folding the paper and (b) with pencil and ruler. Hints:

• Version 1a: Fold two circle diameters which intersect in the circle’s center.
• Version 1b: Can you recreate this construction using pencil and ruler?
• Version 2a: Fold two chords of the circle as well as their perpendicular bisectors which intersect in the center of the circle.
• Version 2b: Can you recreate this construction using pencil and ruler?

Now use GeoGebra in order to recreate the construction you used in version 2b.

Preparations

• Open a new GeoGebra window.
• Switch to Perspectives – Geometry.
• Show the Input Bar (View Menu).

Construction Steps

1		Enter circle c’s equation: x^2 + y^2 = 16.
2		Create chord a of circle c. Aviso: A chord is a segment whose endpoints both lie on the circle.
3		Create midpoint C of chord a.
4		Create perpendicular line b to the chord a through point C. Aviso: You just created the perpendicular bisector of chord a.
5		Create another chord d of circle c.
6		Create midpoint F of chord d.
7		Create perpendicular line e to chord d through point F.
8		Intersect lines b and e to get intersection point G. Aviso: Point G is the center of circle c.
9		Enhance your construction using the Properties dialog.
10		Check your construction for different positions of the chords.

Tasks

• Show the Navigation bar for Construction Steps (View Menu) within the Graphics view of your construction and use it to review the construction steps.
• Insert breakpoints in the Construction protocol to group some of the objects you used (open the Construction Protocol – Show the column Breakpoint). After specifying your breakpoints, check Show Only Breakpoints.
• Export the construction as a dynamic worksheet that includes the Navigation bar (Export dialog – tab Advanced) and save the file as Center_Circle_Solution.html.
• Open the dynamic worksheet you just exported. Use the Navigation bar to review your construction and write down which tools you used in order to construct the center of the circle.

Customizing the Toolbar

You will now learn how to customize GeoGebra’s toolbar so you can limit the number of available tools for your students.

1. In the Tools menu click on Customize Toolbar…

2. The window on the left hand side lists all GeoGebra tools that are part of the default toolbar. If you click on one of the + symbols in front of the tool names the corresponding toolbox is opened. The window on the right hand side contains all available GeoGebra tools.

3. In the left hand side list select the word Separator. Click button Remove > several times until all list entries apart from Move are deleted.

4. In the left hand side list click on the + symbol in front of the Move tool to open the toolbox. Select tool Rotate around Point and click the Remove > button again. The Move tool should now be the only tool left in the list on the left hand side.

5. Close the Move toolbox in the left hand side list by clicking on the – symbol.

6. In the right hand side list select tool Intersect Two Objects and click button < Insert.

7. Repeat step 6 for the other tools you need for constructing a circle’s center (Midpoint or Center, Segment between Two Points, Perpendicular Line).

8. Use the Up and Down buttons to change the order of the tools in the left hand side list.

9. Click Apply once you are done.

10. Your GeoGebra window should now show the customized toolbar.

Task

• Delete all objects apart from the circle.
• Export this updated construction as a dynamic worksheet that includes the customized toolbar and shows the toolbar help (Export dialog – tab Advanced).
• Save the dynamic worksheet as Center_Circle_Construction.html.

Challenge of the Day: Euler’s Discovery

Task

• Construct the following three remarkable points of a triangle: circumcenter, orthocenter and centroid. Create a custom tool for each of these points. Save your custom tools.

• Use your custom tools within one construction to find the relation between these three points as the Swiss mathematician Euler did in the 18th century, obviously without having access to dynamic geometry software ;-)

Circumcenter of a Triangle

Preparations

• Open new GeoGebra window.
• Switch to Perspectives - Geometry.
• Change the labeling setting to New Points Only (menu Options – Labeling).

Construction Steps

1		Create an arbitrary triangle ABC.
2		Create perpendicular bisectors d, e and f for all sides of the triangle. Aviso: The tool Perpendicular Bisector can be applied to an existing segment.
3		Construct intersection point D of the two of the line bisectors.
4		Create a circle with center D through one of the vertices of triangle ABC.
5		Rename point D to Circumcenter.
6		Use the drag test to check if your construction is correct.
7		Create a custom tool for the circumcenter of a triangle. Output objects: point Circumcenter Input objects: points A, B and C Name: Circumcenter Toolbar help: Click on three points
8		Save your custom tool as file circumcenter.ggt.

Orthocenter of a Triangle

Preparations

• Open new GeoGebra window.
• Switch to Perspectives – Geometry.
• Change the labeling setting to New Points Only (menu Options – Labeling).

Construction Steps

1		Create an arbitrary triangle ABC.
2		Create perpendicular lines d, e and f to each side through the opposite vertex of the triangle.
3		Construct intersection point D of two of the perpendicular lines.
4		Rename point D to Orthocenter.
5		Use the drag test to check if your construction is correct.
6		Create a custom tool for the orthocenter of a triangle. Output objects: point Orthocenter Input objects: points A, B and C Name: Orthocenter Toolbar help: Click on three points
7		Save your custom tool as file orthocenter.ggt.

Centroid of a Triangle

Preparations

• Open new GeoGebra window.
• Switch to Perspectives – Geometry.
• Change the labeling setting to New Points Only (menu Options – Labeling).

Construction Steps

1		Create an arbitrary triangle ABC.
2		Create midpoints D, E and F of the triangle sides.
3		Connect each midpoint with the opposite vertex using segments d, e and f.
4		Create intersection point G of two of two of the segments.
5		Rename point G to Centroid.
6		Use the drag test to check if your construction is correct.
7		Create a custom tool for the centroid of a triangle. Output objects: point Centroid Input objects: points A, B and C Name: Centroid Toolbar help: Click on three points
8		Save your custom tool as file centroid.ggt.

What was Euler’s discovery?

Task 1

• Open a new GeoGebra window and import your three custom tools (circumcenter.ggt, orthocenter.ggt and centroid.ggt) into the toolbar.
• Create an arbitrary triangle ABC and apply all three custom tools to the triangle in order to create the circumcenter, orthocenter and centroid within the same triangle.
• Move the vertices of triangle ABC and observe the three remarkable points you just constructed. Which relationship do they have? Use one of GeoGebra’s geometry tools in order to visualize this relationship.

Task 2

• Open an empty GeoGebra window. Customize the toolbar so it only consists of the following tools: Move, Polygon, Line through Two Points, Circle with Center through Point, Circumcenter, Orthocenter and Centroid.
• Export this empty GeoGebra window as a dynamic worksheet that includes the customized toolbar as well as the toolbar help. Come up with instructions that guide your students towards discovering the Euler line in a triangle.