Revision history of "Circle Command"

Diff selection: Mark the radio boxes of the revisions to compare and hit enter or the button at the bottom.
Legend: (cur) = difference with latest revision, (prev) = difference with preceding revision, m = minor edit.
Comments
Tips[edit]
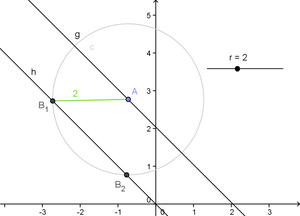
Use circles to fix the distance between two objects[edit]
Circles are a great way to make the distance between two objects constant: If there are two points A and B on two lines g (point A) and h (point B) where A can be moved and B should have the constant distance r to A you can define B as the intersection between the line h and the circle around A with the radius r. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection.