Commentaires:EPM012
012 Retour
|
Le triangle ABC représente une équerre.
On s’intéresse à l’étude du lieu de certains points de l’équerre lorsque les points A et C glissent respectivement sur les demi-droites perpendiculaires [OM) et [OS). |
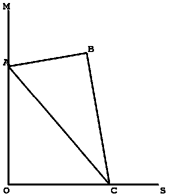
Une réflexion s'impose pour la construction de l'équerre. (Que tout se déplace bien en même temps !) Définir une longueur AC variable, un angleA variable.
Construire les 2 demi-droites perpendiculaires, A sur [OM), C point d'intersection de [OS) et du cercle de centre A et de rayon AC.
Faire tourner C autour de A de angleA, et A autour de C de -angleC, pour définir par intersection le point B.
Sinon au niveau de l'utilisation de GeoGebra, il s'agit d'un problème classique de lieu. On activera donc la trace (version volatile) du point considéré ; ou on définira son lieu Lieu[B,A](version pérenne) pour le lieu de B.
La situation ne précise pas les points dont on cherche le lieu, s'il est flagrant que le lieu de B va être digne d'intérêt, on peut faire remarquer que le milieu B' de [AC] (centre d'un cercle passant par O,A,B et C) va décrire le quart de cercle de centre O de rayon AC/2 situé dans le quadrant SOM.
Quant au lieu de B, il s'agit d'un segment.
Dans un premier temps remarquons que le lieu de B est inclus dans la demi-droite image de la demi-droite [OM) par la rotation de centre O et d'angle angleC (dans le sens horaire).
En effet, dans le cercle de centre B' passant par O,A,B et C les angles \widehat{AOB} et \widehat{ABC} interceptant le même arc (comment marque-ton un arc avec HotEqn ? )AB sont égaux.
Dans un deuxième temps, calculons la longueur OB.
En appliquant la propriété d'Al Kashi dans le triangle OCB, il vient :
OB^2 = CO^2 + CB^2 - 2\times CO\times CB\times \cos(\widehat{OCB})
et dans le triangle OAB :
OB^2 = AO^2 + AB^2 - 2\times AO\times AB\times \cos(\widehat{OAB})
Soit
2 OB^2 = (CO^2 + AO^2) + (CB^2 + AB^2) - 2\times CO\times CB\times \cos(\widehat{OCB})- 2\times AO\times AB\times \cos(\widehat{OAB})
et en utilisant la propriété de Pythagore dans les 2 triangles rectangles AOC et ABC :
2 OB^2 = 2 AC^2 - 2\times CO\times CB\times \cos(\widehat{OCB})- 2\times AO\times AB\times \cos(\widehat{OAB})
Le quadrilatère OACB étant inscriptible dans un cercle, les angles \widehat{OCB} et \widehat{OAB}sont supplémentaires, leurs cosinus sont opposés.
OB^2 = AC^2 - \cos(\widehat{OCB}) (CO \times CB - AO \times AB)
Dans le triangle rectangle OCA CO = CA \cos(\widehat{OCA}) et AO = CA \sin(\widehat{OCA})
Dans le triangle rectangle ABC CB = CA \cos(\widehat{ACB}) et AB = CA \sin(\widehat{ACB})
Soit
OB^2 = AC^2 - AC^2 \cos(\widehat{OCB}) (\cos(\widehat{OCA}) \cos(\widehat{ACB}) - \sin(\widehat{OCA}) \sin(\widehat{ACB}))
OB^2 = AC^2 - AC^2 \cos(\widehat{OCB}) (\cos(\widehat{OCA}+\widehat{ACB} )
OB^2 = AC^2 (1 - (\cos(\widehat{OCB}))^2) = AC^2 (\sin(\widehat{OCB}))^2)
Soit :
OB = AC \sin(\widehat{OCB})
On a
\widehat{OCB} = \widehat{OCB'} + \widehat{ACB} = \widehat{COB'} + \widehat{ACB}
\widehat{COB'} varie de 0 à \Pi/2 donc \widehat{OCB} varie de \widehat{ACB} à \widehat{ACB} + \Pi/2
et donc son sinus varie de \sin(\widehat{ACB}) à \sin(\widehat{ACB}) + \Pi/2) = \cos(\widehat{ACB})
La longueur OB est au plus égale à AC, son minimum est atteint, suivant la valeur d'angleA, lorsque [AC] est dans [OM) ou dans [OS)
si \widehat{ACB} \leq 45° soit angleA \geq 45° ; OB_{min} = AC \sin(\widehat{ACB}) = AB ;
si \widehat{ACB} \geq 45° soit angleA \leq 45° ; OB_{min} = AC \cos(\widehat{ACB}) = BC .
Déclinaison Janvier 2007
Contributions
Philippe Paclet (Florence) a créé les fichiers :
[1] Lieu d'un barycentre donné : c'est dans tous les cas un quart d'ellipse de centre O(avec les complexes)
[2] Lieu du centre de gravité de l'équerre (avec les complexes)
[3] Le problème de l'équerre traité avec les complexes
[4] La figure de Noel (merci) avec un 'curseur circulaire' pour contrôler l'angle en A.
