Algebra desde la Barra de Entrada II

Introducción Operativa
Dando Entrada a Objetos de Definición Algebraica
1. Se les da Nombre a Nuevos Objetos, simplemente anteponiendo su nombre = en la Barra de Entrada a su definición algebraica.
2. Un Producto se establece con un asterisco o espacio entre los factores.
3. ¡GeoGebra es sensible a las minúsculas diferencias!... lo que implica que identifica como distintos los nombres de variables en que solo una mayúscula o un tilde distingue una de otra. Por eso es preciso controlar estas cuestiones tanto al otorgar un nombre como al referirlo.
- Los nombres que otorga GeoGebra, espontáneamente a los objetos creados - sea a partir de una herramienta como desde un comando - presentan ciertas distinciones y así, los de los...
- Puntos son letras mayúsculas. Ejemplo: A = (1, 2) o, en coordenadas polares, B = (2; pi)
- Vectores son letras minúsculas Ejemplo: v = (1, 3)
 Aviso: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
Aviso: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
- Puntos son letras mayúsculas.
- Llevan minúsculas también las...
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados Ejemplo: circunferencia c: (x – 2)^2 + (y – 1)^2 = 16
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados
- Deben anotarse y referirse en minúsculas los nombres de las variables como...
- la independiente x de una función o
- x e y en cualquier expresión - ecuación de una sección cónica, de una inecuación, etc. -. Ejemplo: f(x) = 3*x + 2
4. Para incluir un objeto en una anotación en la Barra de Entrada, es preciso crearlo antes y referirlo por el nombre que lo identifica, recordando distinguirlo con todos los detalles correspondientes (mayúsculas, minúsculas, tildes...). Esto vale tanto para las expresiones algebraicas como para los comandos...
- y = m x + b o y = m f(-b) x + f(b) crea una recta en tanto m como b sean ya:
- números que harán las veces de parámetros (recordar que todo número establecido como tal involucra un deslizador cuyo valor puede modificarse en tanto se lo torne visible en la Vista Gráfica activa.
- Recta[A, B] o Recta[A + b Vector[A, B] , B] crea una recta en tanto exista el punto A y el B y/o el número b.
5. Cada expresión ingresada en la Barra de Entrada se debe confirmar' pulsando la tecla Enter (o Intro como aparece en algunos teclados).
6. Tanto las teclas de atajo (F1) como la opción del Menú de Ayuda, permiten abrir la ventana pertinente para averiguar el modo de empleo de un comando en la Barra de Entrada.
7. Si al ingresar un comando en la Barra de Entrada aparece un error, conviene leer detenidamente el correspondiente mensaje para tener mayores recursos para subsanarlo.
8. Los Comandos se pueden anotar o seleccionar desde la lista próxima a la Barra de Entrada.
9. Tras anotar las dos primeras letras de cualquier comando en la Barra de Entrada, emergen alternativas para su Completado Automático tentativo que permite...
- Seleccionar el adecuado pulsando Enter ( Intro en algunos teclados) para ubicar el cursor entre los corchetes.
- Proseguir anotando las siguientes letras hasta que se despliegue el deseado.
Explorando Relaciones entre Coeficientes y Gráficas en Cuadráticas
En esta propuesta se procurará vincular en sentido directo e inverso, las relaciones entre los coeficientes de una expresión cuadrática y su comportamiento gráfico.
Desafío Reconstructivo
Dados cinco puntos distribuidos al azar, ¿cómo se podría deslizar la gráfica de y = x^2 usando las teclas flecha - Arriba ascendentes / Abajo descendentes y las laterales -> a izquierda y <- derecha - para que la gráfica cruce por la mayor cantidad de tales puntos y/o su distancia a los restantes sea lo menor posible?
Por eso, la segunda condición - su a los restantes sea lo menor posible - es de importancia y requiere, además, una maniobra para establecer estas distancias.
Preparativos
1 Seleccionar la de Álgebra y Gráficos en el Menú Apariencias
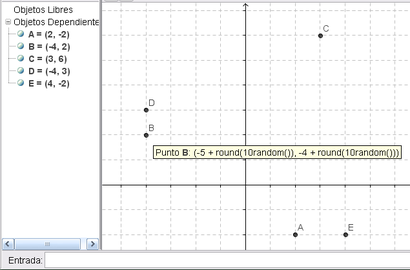
2 Ingresar en la Barra de Entrada, cinco veces esta anotación para dar con puntos al azar:
- (-5 + round(10random()), -4 + round(10random()))
Planteo Aleatorio Puntual
Para completar el planteo del desafío que va a guiar la tarea que relaciona los distintos registros - expresión, ecuación, tabla de valores, representación gráfica... - se pasa a considerar la distribución de los puntos: - ¿Conforman un conjunto aceptable del que se puedan elegir cuatro - o al menos tres - para encontrar una cuadrática que los atraviese?
- Decidir si se van a aceptar como datos los cinco puntos que el azar deparó y...
De este conjunto de puntos serían aceptables, por ejemplo, A, E y C y nunca B y D juntos dado que comparten la ordenada, condición que no puede darse en puntos sobre una parábola.
- Pulsar las teclas Ctrl + R para que el recálculo de los valores aleatorios provoque una reubicación de los puntos en caso de no estar en una posición adecuada para las condiciones del problema
- Copiar las coordenadas de cada punto en un sector de la Hoja de Cálculo que se expondrá con tal fin
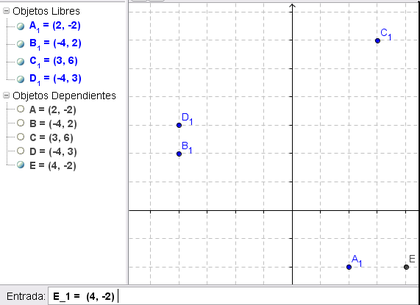
- Definir cinco puntos no aleatorios que tendrán las coordenadas de los que el azar deparó, simplemente empleando la tecla F4 para copiar los valores de cada uno de ellos en otro conjunto con nombres análogos - diferenciados por el subíndice _1 - que no queden afectados por el recálculo del azar.
- A_1 = (2, -2)
- B_1 = (-4, 2)
- C_1 = (3, 6)
- D_1 = (-4, 3)
- E_1 = (4, -2)
- Darle a cada punto vistoso y diverso formato y color
3 Ingresar en la Barra de Entrada la siguiente expresión:
- y = x^2 o
- y = - x^2 (según la concavidad con que se desee tantear)
4 Seleccionar la expresión y...
- Pulsar las teclas Arriba / Abajo u las Izquierda / Derecha
- Registrar el efecto que estas maniobras tienen sobre el gráfico y la expresión correspondiente.
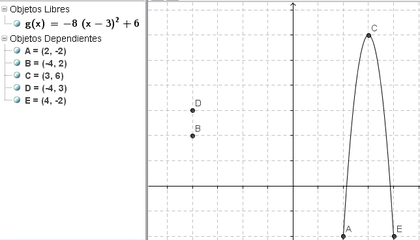
5 Establecer alguna estrategia para lograr que la cuadrática cruce por la mayor cantidad posible de puntos.
En el caso tomado como ejemplo, después de lograr que la representación de la expresión que inicialmente se ingresara como y = - x^2 que permitió hacer coincidir el punto C_1 con el vértice - con (x - 3)² + 6 que solo exigió operar con las teclas de flecha - , se hizo necesario modificar la apertura con un adecuado coeficiente para la expresión - en este caso, 8 para que resultara 8 (x - 3)² + 6 -.
- con formulación canónica asociada a tres
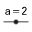 deslizadores - a, h y k - en f(x) = a (x - h)² + k - para tantear los valores que deben tomar cada uno de ellos.
deslizadores - a, h y k - en f(x) = a (x - h)² + k - para tantear los valores que deben tomar cada uno de ellos. - con formulación polinómica asociada a tres
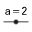 deslizadores - a, b y c en f(x) = a x² + b x + c - para poder desplazarla a través de los cambios que se introduzcan en cada uno de ellos. A continuación se ofrece una breve explicación de esta última maniobra.
deslizadores - a, b y c en f(x) = a x² + b x + c - para poder desplazarla a través de los cambios que se introduzcan en cada uno de ellos. A continuación se ofrece una breve explicación de esta última maniobra.
Coeficientes Deslizables
Para contar con una gráfica que sea posible ajustar a la que atraviese la mayor cantidad de puntos aleatorios distribuidos, además de la que originalmente se ingresó como y = x^2 y que se puede maniobrar con las teclas de flecha, basta con...
- Ingresar sucesivamente en la Barra de Entrada, los valores de partida para a, b y c. Como, por ejemplo
- a = 1 y Enter (Intro en algunos teclados)
- con la misma maniobra, ingresar los valores para b y c - por el momento, b=0 y c = 0 -
- Anotar la expresión dependiente de a, b y c...
- a x^2 + b x + c - - a la que se le puede otorgar un color y estilo que la distinga de la previamente ingresada y = x^2 -
- Dar visibilidad a los números a, b y c con un clic en cada redondelito que aparece a la izquierda de cada uno de ellos en la Vista Algebraica.
Ensayos Preliminares
Pueden llevarse adelante algunos ensayos para corroborar que...
- la gráfica de la expresión ingresada - a x^2 + b x + c - reacciona a los cambios en los valores de los deslizadores como se observa en el registro algebraico en que aparece como Objeto Dependiente expresada como f(x) = a x^2 + bx + c
En cambio...
- mantiene su carácter de objeto libre la que fuera originalmente anotada como y = x^2 , cambiando su representación gráfica y expresión cuando se la selecciona y se opera con las teclas de flecha
Con una y/u otra gráfica se puede procurar una vía sistemática para lograr que cruce por la mayor cantidad de puntos en juego.
Alternativa de Tanteo Geométrico
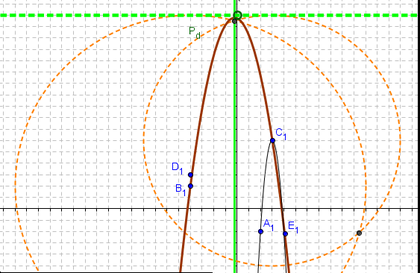
Una alternativa de tanteo geométrico, implicaría seleccionar, digamos, dos de los puntos por los que se pretende que pase la función cuadrática y operar en torno a las condiciones que conocemos de la parábola como... lugar geométrico de los puntos que equidistan de un recta denominada directriz y de un punto llamado foco . Desde esta perspectiva, se puede:
- colocar un punto sobre el EjeY para trazar por allí una paralela al EjeX que será la directriz tentativa
- trazar con centro en cada punto seleccionado, la circunferencia que tiene por radio la distancia de cada uno de ellos a esa directriz tentativa
- establecer los puntos de intersección de cada par de circunferencia y con la
 herramienta correspondiente, trazar la parábola asociada a la cuadrática que se busca que tenga tal intersección como foco y tal paralela como directriz
herramienta correspondiente, trazar la parábola asociada a la cuadrática que se busca que tenga tal intersección como foco y tal paralela como directriz
* esto nos provee de la parábola que pasa por dos de los puntos y, deslizando el punto sobre el EjeY se procura pasar con esta curva por otro de los que estuvieran en juego.
Esta sucesión de maniobras - que se evidencia en la figura - da pie a la subsecuente búsqueda de la fórmula de la cuadrática que se procura y permite inter-relacionar recursos gráficos - geométricos - con los analíticos y algebraicos.
Determinantes Soluciones Algebraicas
Más allá de los tanteos y posibilidades de jugar con las curvas, se puede arribar a la resolución algebraica empleando los comandos correspondientes (básicamente Comando Determinante). Partiendo de la forma de la ecuación:
- y(x) = ax^2 +bx +c
y conocidos tres puntos del plano xy por los que pasa una función polinómica de segundo grado:
- (x_1,y_1), (x_2,y_2), (x_3,y_3)
se cumplirá que:
con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.
Representando el sistema ordenado de forma convencional:
Con lo que podemos calcular los valores de los coeficientes:
Esta sucesión de maniobras, ahora algebraicas, no ya geométricas, queda ilustrada en la figura.
Repertorio de Funciones
Más allá de los polinomios que pueden ingresarse directamente en la Barra de Entrada, es posible apelar a cualquier de los diferentes tipos de funciones disponibles en GeoGebra (sean las trigonométricas, las exponenciales, las de valor absoluto, módulo o resto...). Con las funciones se puede operar como con cualquier otro objeto e incluso combinarse con construcciones geométricas o con datos que se registren en las celdas de una Hoja de Cálculo.
Para profundizar y ampliar lo que se estudia en este tutorial, es aconsejable consultar: