Diferencia entre revisiones de «Tutorial:Bloque de Prácticas»

| Línea 22: | Línea 22: | ||
{{step|num=5}} Completar los detalles del texto dinámico y mejorar los del gráfico para que el escenario gráfico de resolución quede alistado para resolver toda una variedad de problemas. | {{step|num=5}} Completar los detalles del texto dinámico y mejorar los del gráfico para que el escenario gráfico de resolución quede alistado para resolver toda una variedad de problemas. | ||
{{Note|1=Además de cuestiones casi cosméticas, es de importancia, darle a cada uno de los deslizadores un rando de valores y uno de incremento de modo que se puedan representar cada uno de los ejercicios que se destine a este encuadre de resolución gráfica.}} | {{Note|1=Además de cuestiones casi cosméticas, es de importancia, darle a cada uno de los deslizadores un rando de valores y uno de incremento de modo que se puedan representar cada uno de los ejercicios que se destine a este encuadre de resolución gráfica.}} | ||
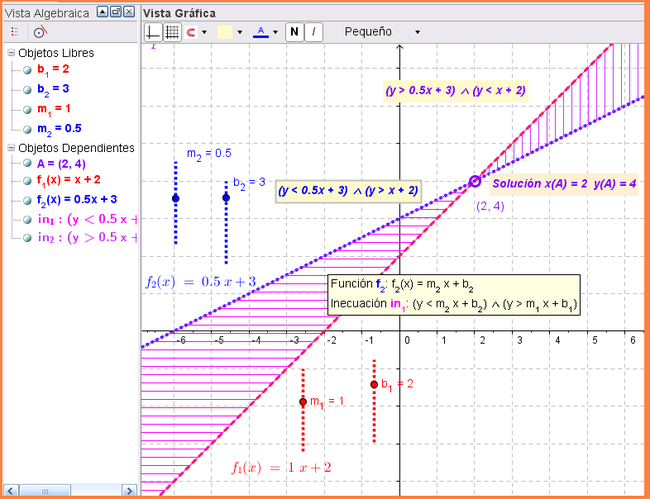
| − | {{step|num=6}} Un desafío adicional sería el de cuestionar cuál de las inecuaciones | + | {{step|num=6}} Un desafío adicional sería el de cuestionar cuál de las inecuaciones se vincula a los sectores sombreados a uno y otro lado del punto de intersección y si hay situaciones en que se modifica esta correspondencia. |
| − | [[ | + | {{Note|1=<br> |
| + | El par de inecuaciones que se ingresan por [[Barra de Entrada]] y también se establece su texto dinámico representativo correspondiente, son... | ||
| + | * in_1: (y < m_2 x + b_2) ∧ (y > m_1 x + b_1) | ||
| + | * in_2: (y > m_2 x + b_2) ∧ (y < m_1 x + b_1) | ||
| + | ... como puede observarse en la figura, en la que además se aprecia que los sombreados respectivos son rayados con un ángulo de 0 y 90 grados.}} | ||
| + | '''[[File:Lineales.PNG|650px|center]]''' | ||
| + | {{step|num=7}} Antes de guardar el boceto del escenario creado, es conveniente dejar anotadas en un archivo de texto asociado, la serie de ejercicios y problemas a resolver empléandolo. | ||
===Challenge=== | ===Challenge=== | ||
Revisión del 06:50 6 ago 2012
Resoluciones Gráficas de Sistemas de (In)Ecuacions
Un sistema de ecuaciones lineales puede quedar diseñado como un escenario para la resolución gráfica de modo tal que en cada caso se ingresen los valores correspondientes y sea posible representar ágilmente una variedad de problemas de tal tipo.
Pasos de Construcción
1 Como se anotarán dos funciones de formato m x + b, es preciso ingresar en primer lugar, desde la Barra de Entrada, cada componente necesario, empezando por...
- m_1 = 1 b_1 = 3
- m_2 = 2 b_2 = 1
... para terminar por:
- m_1 x + b_1
- m_2 x + b_2
Todo esto aparecerá registrado en la Vista Algebraica
2 Los valores de cada parámetro determinará la inclinación y la posición de la recta que representa la ecuación y para que todo sea más fácil de ser identificado, conviene darles los mismos colores contrastantes a los de una y otra ecuación.
- los deslizadores a los que se les asignó orientación Vertical en la casilla correspondiente de la pestaña Deslizador de la Caja de Diálogo de Propiedades,
- el rótulo de cada ecuación de recta a la que, además, se les cambió en nombre por f_1 y f_2 respectivamente.
3 Se puede establecer, con la herramienta ![]() , el punto de intersección entre una y otra función graficada.
, el punto de intersección entre una y otra función graficada.
4 Con la correspondiente herramienta ![]() , se puede establecer el texto en el lugar adecuado de la Vista Gráfica y anotar el texto estático: Solución: x = y seleccionar el nombre del punto de intersección del listado que se despliega a indicar Objetos.
, se puede establecer el texto en el lugar adecuado de la Vista Gráfica y anotar el texto estático: Solución: x = y seleccionar el nombre del punto de intersección del listado que se despliega a indicar Objetos.
- modificar la casilla que contiene el nombre del punto de intersección, digamos A para reemplazarlo por x(A) y
- hacer nuevamente otro tanto para y(A).
5 Completar los detalles del texto dinámico y mejorar los del gráfico para que el escenario gráfico de resolución quede alistado para resolver toda una variedad de problemas.
6 Un desafío adicional sería el de cuestionar cuál de las inecuaciones se vincula a los sectores sombreados a uno y otro lado del punto de intersección y si hay situaciones en que se modifica esta correspondencia.
El par de inecuaciones que se ingresan por Barra de Entrada y también se establece su texto dinámico representativo correspondiente, son...
- in_1: (y < m_2 x + b_2) ∧ (y > m_1 x + b_1)
- in_2: (y > m_2 x + b_2) ∧ (y < m_1 x + b_1)
7 Antes de guardar el boceto del escenario creado, es conveniente dejar anotadas en un archivo de texto asociado, la serie de ejercicios y problemas a resolver empléandolo.
Challenge
Create a similar construction that allows for visualizing the graphical solution of a system of quadratic polynomials.
Translating Pictures
In this activity you are going to use the following tools and commands. Make sure you know how to use each tool and command before you begin.
| Insert Image | |
| A = (1, 1) | |
| Polygon | |
| Vector[O, P] | |
| Vector Between Two Points | |
| Translate Object By Vector | |
| Move | |
| Text |
Construction Steps
1. Open a new GeoGebra window. Show the Algebra View, Input Bar, coordinate axes, and grid. In the Options Menu set the point capturing to Fixed to Grid.
2. Insert picture A_3b_Bart.png into the first quadrant.
3. Create points A = (1, 1), B = (3, 1), and D = (1, 4).
4. Set point A as the first, B as the second, and D as the fourth corner point of the picture (Properties Dialog, tab Position).
5. Create triangle ABD.
6. Create point O = (0, 0) and point P = (3, -2).
7. Create vector u = Vector[O, P]. {{hint|You could also use [[tool Vector Between Two Points.}}
8. Translate the picture by vector u using Translate Object by Vector.
9. Translate the three corner points A, B, and D by vector u.
10. Create triangle A'B'D'.
11. Hide point O so it can’t be moved accidentally. Change the color and size of objects to enhance your construction.
Challenge
Insert dynamic text that shows
- the coordinates of points A, B, C, A', B', and D'.
- the coordinates of vector u.
Constructing a Slope Triangle
In this activity you are going to use the following tools and algebraic input. Make sure you know how to use each tool and the syntax for algebraic input before you begin.
| Line Through Two Points | |
| Perpendicular Line | |
| Intersect Two Objects | |
| Polygon | |
| rise = y(B) - y(A) | |
| run = x(B) - x(A) | |
| slope = rise / run | |
| Text | |
| Midpoint or Center | |
| Move |
Construction Steps
1. Show the Algebra View, coordinate axes and the grid. Set point capturing to Fixed to Grid and the labeling to All new objects.
2. Create line a through two points A and B.
3. Construct a perpendicular line b to the y-axis through point A.
4. Construct a perpendicular line c to the x-axis through point B.
5. Intersect perpendicular lines b and c to get intersection point C.
6. Create polygon ACB and hide the labels of the sides.
7. Calculate the rise: rise = y(B) - y(A)
8. Calculate the run: run = x(B) - x(A)
9. Enter the following equation into the input bar to calculate the slope of line a: slope = rise / run
10. Insert dynamic text: rise = and select rise from Objects, run = and select run from Objects, slope = and select slope from Objects
11. Change properties of objects in order to enhance your construction.
Challenge 1: Insert a dynamic text that contains a fraction
Using LaTeX formulas, text can be enhanced to display fractions, square roots, or other mathematical symbols.
- Activate tool Insert text and click on the Graphics View.
- Type slope = into the Insert text window’s input bar.
- Check LaTeX formula and select Roots and Fractions a/b from the dropdown list.
- Place the cursor within the first set of curly braces and replace a by number rise from the Objects drop-down list.
- Place the cursor within the second set of curly braces and replace b by number run from the Objects drop-down list.
- Click OK.
Challenge 2: Attach text to an object
Whenever an object changes its position, attached text adapts to the movement and follows along.
- Create midpoint D of the vertical segment using tool Midpoint or center.
- Create midpoint E of the horizontal segment.
- Open the Properties Dialog and select text1 (rise = …). Click on tab Position and select point D from the drop-down list next to Starting point.
- Select text2 (run = …) in the Properties Dialog and set point E as starting point.
- Hide the midpoints D and E.
Exploring the Louvre Pyramid
In this activity you are going to use the following tools and some algebraic input. Make sure you know how to use every single tool and the syntax for algebraic input before you begin. Also, check if you have the picture A_3d_Louvre.jpg saved on your computer.
| Insert Picture | |
| Line Through Two Points | |
| Slope | |
| Angle | |
| New Point | |
| Perpendicular Line | |
| Intersect Two Objects | |
| Show/Hide Object | |
| Segment Between Two Points | |
| Move |
The Louvre in Paris is one of the most visited and famous art museums in the world. The building holds some of the world's most famous works of art, such as Leonardo da Vinci's Mona Lisa. In 1989 the main entrance of the museum was renovated and a glass pyramid was built (from http://en.wikipedia.org/wiki/Louvre, February 20, 2008).
Determine the slope of the pyramid’s faces
1. Set point capturing off. Set the decimal places to 1. Change the labeling setting to All new objects (menu Options).
2. Insert the picture A_3d_Louvre.jpg into the first quadrant of the coordinate system. The left lower corner should match the origin.
3. Reduce the filling of the picture (about 50%) and set it as background image (Properties Dialog).
4. Create a line through two points with the first point at the base and the second point at the vertex of the pyramid.
5. Use the Slope Tool to get slope triangle of line.
6. Task: Determine the slope of the pyramid’s faces in percent.
7. Create the angle between the x-axis and the line. Task: Determine the inclination angle for the pyramid’s face.
Challenge
The pyramid’s base is a square with a side length of 35 meters. Determine the height of the pyramid using similar triangles.
1. Create a new point C on the line.
2. Construct the slope triangle of the line using points C and B at the pyramid’s vertex.
3. Use segments to connect point D with points B and C.
4. Move point C along the line until the horizontal segment of the triangle matches the level of the road in front of the pyramid.
5. Task: Calculate the height of the pyramid using similar triangles.
Check your answer with GeoGebra
6. Show name and values of segments height and halfBase.
7. Drag point C until the horizontal segment has length 35/2 = 17.5.
8. Check if the height of the pyramid matches your answer.
Comment
By implementing the instructions above you were able to graphically determine the approximate value for the pyramid’s height. In reality, the Louvre pyramid has a base length of 35 m and a height of 21.65 m. Its faces have a slope of 118% and an inclination angle of bout 52° (from http://de.wikipedia.org/wiki/Glaspyramide_im_Innenhof_des_Louvre#Daten, February 22, 2008).