Difference between revisions of "Comments:Circle Command"

From GeoGebra Manual
m (added Italic font for objects) |
|||
| Line 4: | Line 4: | ||
===Use circles to fix the distance between two objects=== | ===Use circles to fix the distance between two objects=== | ||
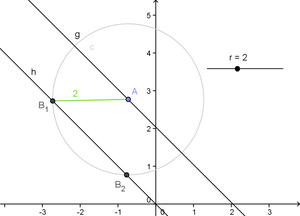
| − | Circles are a great way to make the distance between two objects constant: If there are two points A and B on two lines g (point A) and h (point B) where A can be moved and B should have the constant distance r to A you can define B as the intersection between the line h and the circle around A with the radius r. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection. | + | Circles are a great way to make the distance between two objects constant: If there are two points ''A'' and ''B'' on two lines ''g'' (point ''A'') and ''h'' (point ''B'') where ''A'' can be moved and ''B'' should have the constant distance ''r'' to ''A'' you can define ''B'' as the intersection between the line ''h'' and the circle around ''A'' with the radius ''r''. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection. |
[[File:Fixed_Distance_With_Circle.png|thumb|300px|center|An illustration of the described technique to fix the distance between two points ''A'' and ''B<sub>1</sub>'']] | [[File:Fixed_Distance_With_Circle.png|thumb|300px|center|An illustration of the described technique to fix the distance between two points ''A'' and ''B<sub>1</sub>'']] | ||
[[Category:Commands]] | [[Category:Commands]] | ||
Revision as of 01:26, 18 October 2009
Tips
Use circles to fix the distance between two objects
Circles are a great way to make the distance between two objects constant: If there are two points A and B on two lines g (point A) and h (point B) where A can be moved and B should have the constant distance r to A you can define B as the intersection between the line h and the circle around A with the radius r. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection.