Diferencia entre revisiones de «Comando ResoluciónC»

De GeoGebra Manual
| Línea 3: | Línea 3: | ||
<small>Este [[Comandos#Comandos Restringidos a la Vista CAS (Versión 4.2)|comando]], que lista soluciones [http://es.wikipedia.org/wiki/N%C3%BAmeros_reales#Tipos_de_n.C3.BAmeros_reales <small>'''ℝ'''</small>eales] y/o [[Números Complejos|<small>'''ℂ'''</small>omplejas]] de sistema/ecuaciones respecto a la variable principal o la(s) indicada(s), opera incluso con literales.</small> | <small>Este [[Comandos#Comandos Restringidos a la Vista CAS (Versión 4.2)|comando]], que lista soluciones [http://es.wikipedia.org/wiki/N%C3%BAmeros_reales#Tipos_de_n.C3.BAmeros_reales <small>'''ℝ'''</small>eales] y/o [[Números Complejos|<small>'''ℂ'''</small>omplejas]] de sistema/ecuaciones respecto a la variable principal o la(s) indicada(s), opera incluso con literales.</small> | ||
;ResoluciónC[ <Ecuación> ]:Lista las soluciones [http://es.wikipedia.org/wiki/N%C3%BAmeros_reales#Tipos_de_n.C3.BAmeros_reales <small><small>'''ℝ'''</small></small>eales] y/o [[Números Complejos|<small><small>'''ℂ'''</small></small>omplejas]] de la ecuación o sistema respecto a la variable principal | ;ResoluciónC[ <Ecuación> ]:Lista las soluciones [http://es.wikipedia.org/wiki/N%C3%BAmeros_reales#Tipos_de_n.C3.BAmeros_reales <small><small>'''ℝ'''</small></small>eales] y/o [[Números Complejos|<small><small>'''ℂ'''</small></small>omplejas]] de la ecuación o sistema respecto a la variable principal | ||
| − | :{{Examples|1=<br>'''<code><nowiki>ResoluciónC[x^2 = -1]</nowiki></code>''' da '''''{x = ''ί'', x = -''ί'' }''''', soluciones de ''x<sup>2</sup> = -1''<br><br>'''<code><nowiki>l_c := ResoluciónC[t^2 - a, t]</nowiki></code>''' da, siendo '''<code>t</code>''' la variable principal y '''<code>a</code>''' un valor de '''5''' de un deslizador '''''a''''' animadamente cambiante:<br>l_c := '''{''' ''t'' = ί $\sqrt{5 \; }, \; t = -ί \sqrt{5 \; }$ '''}''' | + | :{{Examples|1=<br>'''<code><nowiki>ResoluciónC[x^2 = -sqrt(-1)]</nowiki></code>''' da:<br> '''{''' x = $\frac{(1- ί) \;\sqrt{2} \; }{2}$, x = -$\frac{(1- ί) \;\sqrt{2} \; }{2}$'''}'''<br><br>'''<code><nowiki>ResoluciónC[x^2 = -1]</nowiki></code>''' da '''''{x = ''ί'', x = -''ί'' }''''', soluciones de ''x<sup>2</sup> = -1''<br><br>'''<code><nowiki>l_c := ResoluciónC[t^2 - a, t]</nowiki></code>''' da, siendo '''<code>t</code>''' la variable principal y '''<code>a</code>''' un valor de '''5''' de un deslizador '''''a''''' animadamente cambiante:<br>l_c := '''{''' ''t'' = ί $\sqrt{5 \; }, \; t = -ί \sqrt{5 \; }$ '''}''' |
}} | }} | ||
:{{OJo|1=De omitirse el segundo miembro de la ecuaciòn, se supone igual a '''''0'''''}}<!-- | :{{OJo|1=De omitirse el segundo miembro de la ecuaciòn, se supone igual a '''''0'''''}}<!-- | ||
Revisión del 00:29 13 feb 2013
ResoluciónC
Categorías de Comandos (todos)
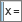 De Vista CAS ComputaciónAlgebraicaSimbólica
De Vista CAS ComputaciónAlgebraicaSimbólica
Este comando, que lista soluciones ℝeales y/o ℂomplejas de sistema/ecuaciones respecto a la variable principal o la(s) indicada(s), opera incluso con literales.
- ResoluciónC[ <Ecuación> ]
- Lista las soluciones ℝeales y/o ℂomplejas de la ecuación o sistema respecto a la variable principal
- Ejemplos:
ResoluciónC[x^2 = -sqrt(-1)]da:
{ x = $\frac{(1- ί) \;\sqrt{2} \; }{2}$, x = -$\frac{(1- ί) \;\sqrt{2} \; }{2}$}ResoluciónC[x^2 = -1]da {x = ί, x = -ί }, soluciones de x2 = -1l_c := ResoluciónC[t^2 - a, t]da, siendotla variable principal yaun valor de 5 de un deslizador a animadamente cambiante:
l_c := { t = ί $\sqrt{5 \; }, \; t = -ί \sqrt{5 \; }$ }
 Atención: De omitirse el segundo miembro de la ecuaciòn, se supone igual a 0
Atención: De omitirse el segundo miembro de la ecuaciòn, se supone igual a 0
- ResoluciónC[ <Ecuación>, <Variable> ]
- Lista las soluciones ℝeales y/o ℂomplejas de la ecuación respecto de la variable indicada.
- Ejemplos:
ResoluciónC[a^2 = -1, a]da {a = i, a = - i }, soluciones ℂomplejas de a2 = -1.ResoluciónC[v²+4,v]da {v = 2 i , v = - 2 i}
.
- ResoluciónC[ <Lista de Ecuaciones>, <Lista de Variables> ]
- Lista las soluciones ℝeales y/o ℂomplejas del sistema de ecuaciones respecto a variable(s) listada(s).
- Ejemplo:
ResoluciónC[{y^2 = x - 1, x = 2 * y - 1}, {x, y}]da
{{x = 1 + 2 i, y = 1 + i}, {x = 1 - 2 ί, y = 1 - i}}, las soluciones ℂomplejas de y2 = x y de x = 2 * y - 1 - Nota:
- El símbolo de los ℂomplejos, ί, se obtiene pulsando Alt +i.
- Revisar también los comandos Resuelve y SolucionesC.
- Ver además la pista Contando Aleatorias Resoluciones




