Difference between revisions of "FractionalPart Function"

From GeoGebra Manual
m (formatting) |
m (added different results for CAS and AV) |
||
| Line 3: | Line 3: | ||
;fractionalPart( <Expression> ) :Returns the fractional part of the expression. | ;fractionalPart( <Expression> ) :Returns the fractional part of the expression. | ||
{{example| 1=<div> | {{example| 1=<div> | ||
| − | *<code><nowiki>fractionalPart( 6 / 5 )</nowiki></code> yields <math>\frac{1}{5}</math>, | + | *<code><nowiki>fractionalPart( 6 / 5 )</nowiki></code> yields <math>\frac{1}{5}</math> in ''CAS View'', 0.2 in ''Algebra View'' |
| − | *<code><nowiki>fractionalPart( 1/5 + 3/2 + 2 )</nowiki></code> yields <math>\frac{7}{10}</math>. | + | *<code><nowiki>fractionalPart( 1/5 + 3/2 + 2 )</nowiki></code> yields <math>\frac{7}{10}</math> in ''CAS View'', 0.7 in ''Algebra View'' |
</div>}} | </div>}} | ||
{{Note|1=<br> | {{Note|1=<br> | ||
Revision as of 12:47, 31 March 2015
- fractionalPart( <Expression> )
- Returns the fractional part of the expression.
Example:
fractionalPart( 6 / 5 )yields \frac{1}{5} in CAS View, 0.2 in Algebra ViewfractionalPart( 1/5 + 3/2 + 2 )yields \frac{7}{10} in CAS View, 0.7 in Algebra View
Note:
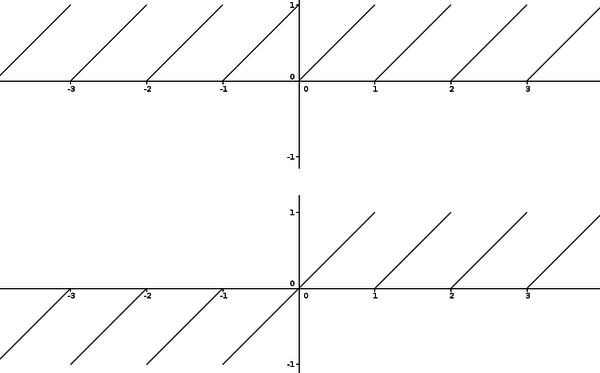
In Mathematics fractional part function is defined sometimes as
- x-\lfloor x\rfloor
In other cases as
- sgn(x)(\mid x\mid-\lfloor \mid x\mid\rfloor) .
GeoGebra uses the second definition (also used by Mathematica).
To obtain the first function you may use f(x) = x - floor(x)