Differenze tra le versioni di "Funzione partefrazionaria"

Da GeoGebra Manual.
Bot (discussione | contributi) m (Bot: Sostituzione automatica (-{{betamanual|version=4.2}} + )) |
|||
| Riga 2: | Riga 2: | ||
{{function|fractionalPart|partefrazionaria}} | {{function|fractionalPart|partefrazionaria}} | ||
;partefrazionaria(Espressione) : Restituisce la parte frazionaria dell'espressione indicata. | ;partefrazionaria(Espressione) : Restituisce la parte frazionaria dell'espressione indicata. | ||
| − | {{ | + | {{examples| 1=<div> |
| − | *<code><nowiki>partefrazionaria( 6 / 5 )</nowiki></code> restituisce <math>\frac{1}{5}</math>, | + | *<code><nowiki>partefrazionaria( 6 / 5 )</nowiki></code> restituisce <math>\frac{1}{5}</math> in ''vista CAS'', 0.2 in ''vista Algebra'' |
| − | *<code><nowiki>partefrazionaria( 1/5 + 3/2 + 2 )</nowiki></code> restituisce <math>\frac{7}{10}</math>. | + | *<code><nowiki>partefrazionaria( 1/5 + 3/2 + 2 )</nowiki></code> restituisce <math>\frac{7}{10}</math> in ''vista CAS'', 0.7 in ''vista Algebra''. |
</div>}} | </div>}} | ||
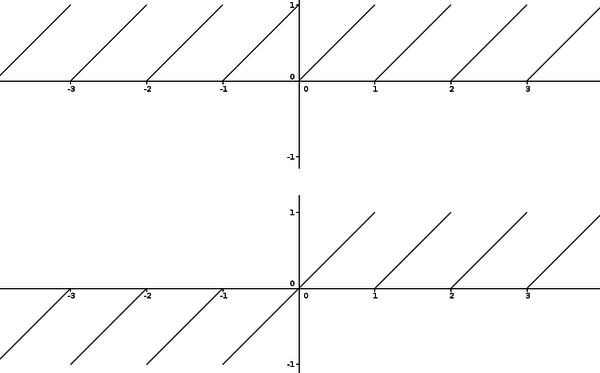
| − | {{note|1=In Matematica la funzione parte frazionaria | + | {{note|1=In Matematica la funzione parte frazionaria può essere definita come <math>x-\lfloor x\rfloor </math>, oppure come <math>sgn(x)(\mid x\mid-\lfloor \mid x\mid\rfloor) </math>. GeoGebra utilizza la seconda definizione (come Mathematica). Per ottenere la prima funzione basta utilizzare <code>f(x) = x - floor(x)</code>. |
| − | Vedere [[Funzioni e operatori predefiniti]].}} | + | Vedere anche [[Funzioni e operatori predefiniti]].}} |
Versione delle 12:41, 31 mar 2015
- partefrazionaria(Espressione)
- Restituisce la parte frazionaria dell'espressione indicata.
Esempi:
partefrazionaria( 6 / 5 )restituisce \frac{1}{5} in vista CAS, 0.2 in vista Algebrapartefrazionaria( 1/5 + 3/2 + 2 )restituisce \frac{7}{10} in vista CAS, 0.7 in vista Algebra.
Note: In Matematica la funzione parte frazionaria può essere definita come x-\lfloor x\rfloor , oppure come sgn(x)(\mid x\mid-\lfloor \mid x\mid\rfloor) . GeoGebra utilizza la seconda definizione (come Mathematica). Per ottenere la prima funzione basta utilizzare
f(x) = x - floor(x).
Vedere anche Funzioni e operatori predefiniti.Commenti
Le seguenti immagini illustrano le due possibili definizioni per la funzione parte frazionaria. GeoGebra utilizza la seconda definizione.