Différences entre versions de « Points et Vecteurs »

| Ligne 7 : | Ligne 7 : | ||
{{exemple|1=<br/> | {{exemple|1=<br/> | ||
* Pour définir un point P ou un vecteur u en coordonnées cartésiennes validez <code><nowiki>P = (1, 0) ou u = (0, 5)</nowiki></code>. | * Pour définir un point P ou un vecteur u en coordonnées cartésiennes validez <code><nowiki>P = (1, 0) ou u = (0, 5)</nowiki></code>. | ||
| − | * Pour définir un point Q ou un vecteur v en coordonnées polaires, validez <code><nowiki>Q = (1; 0°) ou v = (5; 90°)</nowiki></code>. | + | * Pour définir un point Q ou un vecteur v en coordonnées polaires, validez <code><nowiki>Q = (1; 0°) ou v = (5; 90°)</nowiki></code>.}} |
| − | Les lectures des coordonnées d'un point A (par exemple ) se font par : | + | Le menu contextuel d'un point (ou d'un vecteur) du plan propose la bascule d'affichage ''Coordonnées cartésiennes'' <> ''Coordonnées polaires''. |
| + | |||
| + | Les lectures des coordonnées d'un point A (par exemple ) du plan se font par : | ||
* x(A) et y(A) pour les coordonnées cartésiennes, | * x(A) et y(A) pour les coordonnées cartésiennes, | ||
* Longueur[A] et Angle[A] pour les coordonnées polaires. | * Longueur[A] et Angle[A] pour les coordonnées polaires. | ||
| − | + | ||
{{note|Vous devez utiliser un point-virgule pour séparer les coordonnées polaires. Si vous ne tapez pas le symbole degré, GeoGebra considérera que l’angle est entré en radian.}} | {{note|Vous devez utiliser un point-virgule pour séparer les coordonnées polaires. Si vous ne tapez pas le symbole degré, GeoGebra considérera que l’angle est entré en radian.}} | ||
| Ligne 32 : | Ligne 34 : | ||
::{{Exemple|1=<code>A=(1;45°;30°)</code> }} | ::{{Exemple|1=<code>A=(1;45°;30°)</code> }} | ||
<center>[[Image:Spheriques.PNG|300px]]</center> | <center>[[Image:Spheriques.PNG|300px]]</center> | ||
| + | |||
| + | Le menu contextuel d'un point (ou d'un vecteur) de l'espace propose la bascule d'affichage ''Coordonnées cartésiennes'' <> ''Coordonnées sphériques''. | ||
| + | |||
| + | Les lectures des coordonnées d'un point A (par exemple ) de l'espace se font par : | ||
| + | * x(A) , y(A) et z(A) pour les coordonnées cartésiennes, | ||
| + | * Longueur[A] , arg(A) et alt(A) pour les coordonnées sphériques. | ||
| + | |||
</div>}} | </div>}} | ||
Version du 3 mai 2015 à 09:45
Les points et vecteurs peuvent être créés dans le champ de Saisie en coordonnées cartésiennes (le séparateur est la virgule) ou polaires (le séparateur est le point-virgule) (voir Nombres_et_Angles). Les points peuvent être créés en utilisant, par exemple, les outils ![]() Point,
Point, ![]() Représentant ou
Représentant ou ![]() Vecteur et une variété de commandes.
Vecteur et une variété de commandes.
- Pour définir un point P ou un vecteur u en coordonnées cartésiennes validez
P = (1, 0) ou u = (0, 5). - Pour définir un point Q ou un vecteur v en coordonnées polaires, validez
Q = (1; 0°) ou v = (5; 90°).
Le menu contextuel d'un point (ou d'un vecteur) du plan propose la bascule d'affichage Coordonnées cartésiennes <> Coordonnées polaires.
Les lectures des coordonnées d'un point A (par exemple ) du plan se font par :
- x(A) et y(A) pour les coordonnées cartésiennes,
- Longueur[A] et Angle[A] pour les coordonnées polaires.
- Exemple :
A1 = (1, 0).
Un point peut être défini
- par ses 3 coordonnées cartésiennes :
- Exemple :
C=(1,2,3)
- par ses 3 coordonnées sphériques :
- rayon-longitude-latitude
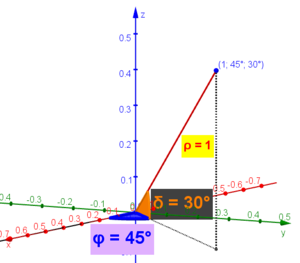
- on nomme les coordonnées (ρ, φ, δ),
- où ρ désigne la distance du point à l'origine,
- φ désigne la longitude (angle mesuré depuis l'axe des x, entre 0° et 360°)
- et δ la latitude, l'angle depuis le plan xOy (entre -90° et 90°)
- Exemple :
A=(1;45°;30°)
Le menu contextuel d'un point (ou d'un vecteur) de l'espace propose la bascule d'affichage Coordonnées cartésiennes <> Coordonnées sphériques.
Les lectures des coordonnées d'un point A (par exemple ) de l'espace se font par :
- x(A) , y(A) et z(A) pour les coordonnées cartésiennes,
- Longueur[A] , arg(A) et alt(A) pour les coordonnées sphériques.
Dans GeoGebra, vous pouvez aussi faire des calculs avec des points et des vecteurs.
- Vous pouvez créer le milieu M entre deux points A et B en validant
M = (A + B) / 2dans le champ de saisie. - Vous pouvez calculer la norme/longueur d'un vecteur v en validant
norme = sqrt(v * v)dans le champ de saisie. - Si A = (a,b), alors A+1 retourne (a+1,b+1). Si A est un nombre complexe a+bi, alors A+1 retourne a+1+bi.
Produit vectoriel
Pour deux points ou vecteurs (a, b) ⊗ (c, d) retourne la cote du produit vectoriel (a, b, 0) ⊗ (c, d, 0) en tant que simple nombre. Un syntaxe semblable est valide pour des listes, mais dans ce cas, le résultat est une liste.
{1, 2} ⊗ {4, 5}retourne {0, 0, -3}{1, 2, 3} ⊗ {4, 5, 6}retourne {3, 6, -3}.




