Diferencia entre revisiones de «Tutorial:Preparando Herramientas Propias en la Barra»

m (gramatic) |
m (link) |
||
| Línea 82: | Línea 82: | ||
Tras haber guardado una herramienta, es sencillo tanto reutilizarla en futuras construcciones, importándola a toda nueva ventana, como recuperarla para emplearla en otro equipo de destino. Basta con... | Tras haber guardado una herramienta, es sencillo tanto reutilizarla en futuras construcciones, importándola a toda nueva ventana, como recuperarla para emplearla en otro equipo de destino. Basta con... | ||
| − | {{Step|num=1|}} En la nueva ventana, si la nueva herramienta no apareciera, recurrir al [[Archivo:Menu Open.png]] [[ | + | {{Step|num=1|}} En la nueva ventana, si la nueva herramienta no apareciera, recurrir al [[Archivo:Menu Open.png]] [[Comentarios:Menúes#Abre...|''Abre...'']] del [[Comentarios:Menúes|Menú Archivo]] y seleccionar el archivo '''''ggt''''' del directorio en que se hubiera guardado. |
{{Step|num=2|}} Al pulsar el botón ''Abre'', una vez seleccionado el archivo correspondiente a la herramienta requerida, se pasa a importarla para tenerla disponible en la ventana de trabajo como una más de la [[:Categoría:Iconos|''barra'']]. | {{Step|num=2|}} Al pulsar el botón ''Abre'', una vez seleccionado el archivo correspondiente a la herramienta requerida, se pasa a importarla para tenerla disponible en la ventana de trabajo como una más de la [[:Categoría:Iconos|''barra'']]. | ||
Revisión del 08:23 27 mar 2020
Instrumentarse gracias al Teorema de Pitágoras
El desafío es encontrar el modo de controlar si el mecanismo empleado para obtener un cuadrado equivalente - de igual área - a un rectángulo ofrecido es eficaz en todos los casos. Esto requiere una justificación argumental según las reglas de juego del quehacer matemático.
Preparativos
En el Menú Apariencias, es preciso seleccionar la adecuada, por ejemplo, Algebra y Gráficos y:
- dejar activa la Barra de Estilo
- ocultar los ejes de coordenadas.
- en el Menú de Opciones, establecer un rotulado tal que lleven etiquetas... Solo los puntos nuevos
- en el Menú Vista, seleccionar la Hoja de Cálculo.
Pasos de Construcción
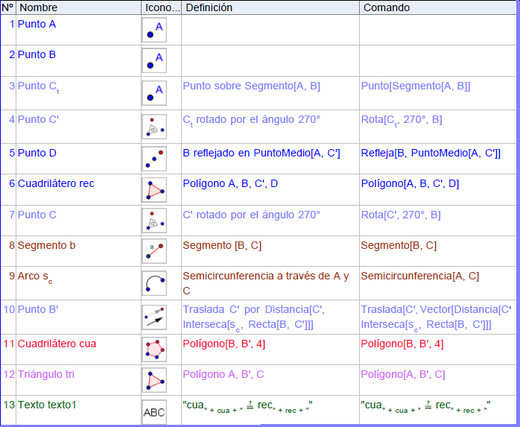
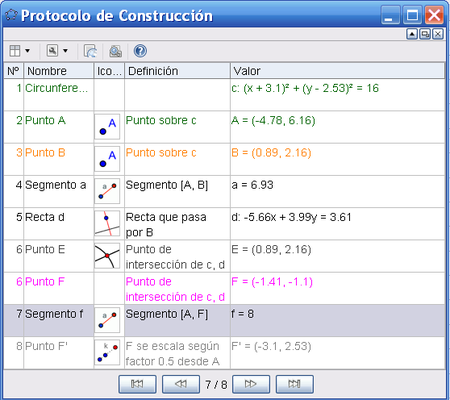
El recorte del Protocolo de Construcción que aparece a continuación, registra los pasos para plantear el escenario de trabajo.
La secuencia de pasos culmina con los retoques y ajustes para que el escenario dinámico resulte ilustrativo.
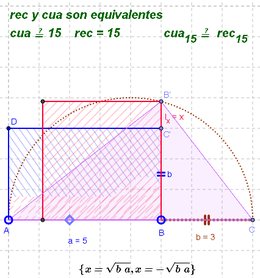
Analizando el Mecanismo
En el escenario planteado, los puntos:
- A y B permiten, al desplazarse, determinar la mayor o menor longitud de la base del rectángulo y
- el que se denomina C_1 - representado por un rombo hueco en el dibujo -, establece la altura que tendrá, como fracción de la base.
Es conveniente rehacer el escenario delante de los destinatarios y centrar el desafío en el análisis del mecanismo. explorando y controlando resultados.
Sumando Registros: La Hoja de Cálculo
La Hoja de Cálculo puede contener en cada celda, los valores que ponen algebraicamente en evidencia el quid de la eficacia general.
Así, se pueden ubicar los distintos valores en cada celda:
- en la primera fila, se disponen los valores de:
- a, b, a b así como l_x² (la media armónica entre a y b) y
- la expresión que explica las relaciones en juego - (x² + a²) + (x² + b²) = (a + b)² - que dará un resultado apenas se la ingrese.
Para analizar la expresión, se debe tener en cuenta que:
- cada una de las sumas entre paréntesis en el primer miembro, se corresponden con el cuadrado de uno y otro cateto del triángulo naranja - dado que x es su altura a la hipotenusa y a y b, la base y altura del rectángulo respectivamente -
- el segundo miembro presenta el cuadrado de la hipotenusa del triángulo naranja compuesta por a y b.
El valor que aparecerá en la celda en que se vuelca esta expresión será justamente el cuadrado de la media armónica mencionada, que da lado al cuadrado equivalente al rectángulo de área a b.
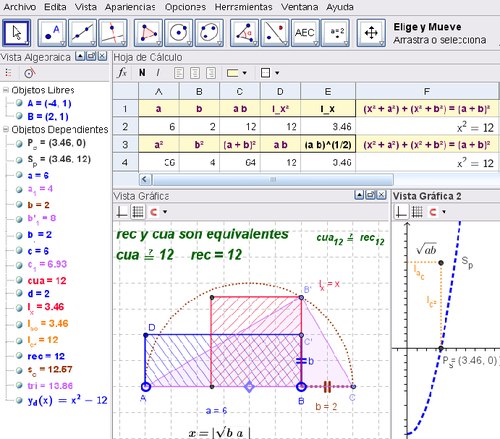
Más Registros: Gráfico Analizado en la Segunda Vista Gráfica
Como se aprecia en la figura previa, contando con la función que se ilustra en la segunda Vista Gráfica se establece y analiza la diferencia de áreas a partir de:
- la Función(x² - ab, 0, a + b) que permite determinar el cero real en que el cuadrado de lado x² resulta equivalente al rectángulo a * b
- el punto de intersección entre la Función(x² - ab, 0, a + b) y el eje positivo de las abscisas - P_s = Interseca(y_d, Semirrecta((0, 0), (1, 0))) -
- la abscisa de P_s = Interseca(y_d, Semirrecta((0, 0), (1, 0))) - x(P_s) coincidente con el valor de \sqrt{a b} -
- el punto S_p = (x(P_s), x(P_s)²) de ordenada igual al valor del área del cuadrado equivalente al rectángulo a x b
- se justifica en la construcción geométrica a expensas del Teorema de Pitágoras - que instrumenta el mecanismo y la argumentación que lo valida -
- se retoma en la Vista Algebraica,
- se organiza y recalcula en la Hoja de Cálculo
- se analiza en la representación de la función en la segunda Vista Gráfica
Para Explorar el Escenario
Es conveniente dejar tendido el escenario dinámico para que los destinatarios puedan concentrarse en la exploración experimental y conceptual más que en los preparativos de requerimiento meramente operativo. Es posible ensayar en el esbozo de aplicación al pie...
Preparación de Herramientas Propias
GeoGebra permite crear herramientas propias. Esto resulta particularmente útil si se va a reiterar un mecanismo o se quiere dejar disponible lo necesario para agilizarle una maniobra a principiantes, obviando así la necesidad de alcanzar un elevado dominio operativo previo al quehacer matemático en juego.
A partir de la Construcción
Si a partir de la construcción previa se deseara preparar una herramienta que trace la media armónica de dos segmentos (en el caso previo, la base y la altura del rectángulo de partida), convendría mantener solo los elementos necesarios y eliminar los restantes.
Así, valdría dejar exclusivamente en par de segmentos de partida y, desde ya, el resultante de salida.
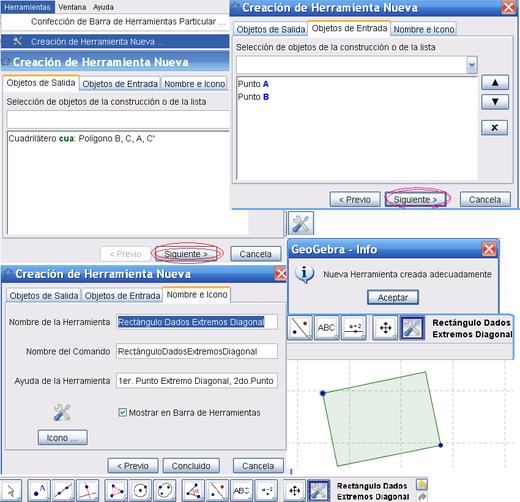
Creando una Herramienta
1 En el Menú de Herramientas, basta con seleccionar ![]() Creación de Herramienta Nueva… para abrir la ventana de diálogo correspondiente.
Creación de Herramienta Nueva… para abrir la ventana de diálogo correspondiente.
2 Como aparece por omisión activa la pestaña Objetos de salida, especificarlos sea con un clic directo sobre el o los objetos (en este caso, el segmento l_x) o desde el listado desplegable al pulsar la flechita próxima al campo de entrada.
3 Seleccionados el o los objetos de salida, pulsar el botón Siguiente > para activar la pestaña Objetos de entrada que aparecerá automáticamente completada, en este caso, con los puntos necesarios (A y B).
4 Seleccionados los objetos de entrada, pulsar el botón Siguiente > para activar la pestaña Nombre e Icono y completar los datos correspondientes en cada campo, incluyendo el de Ayuda.
5 Pulsar el botón Completado para cerrar la ventana de diálogo.
6 Conviene poner a prueba la nueva herramienta creando el segmento correspondiente a la media geométrica a partir de otros elementos de entrada.
Guardando e Importando las Nuevas Herramientas
Guardando la Nueva Herramienta
1 En el Menú de Herramientas, se debe seleccionar ![]() Gestión de herramientas para abrir el cuadro de diálogo.
Gestión de herramientas para abrir el cuadro de diálogo.
2 Basta seleccionar, por su nombre, la herramienta creada y pulsar el botón ![]() Guarda Como… para guardarla, con el nombre que se elija al que se añadirá la extensión ggt, y dejarla disponible para futuras construcciones, al menos en el equipo en que se estuviera operando.
Guarda Como… para guardarla, con el nombre que se elija al que se añadirá la extensión ggt, y dejarla disponible para futuras construcciones, al menos en el equipo en que se estuviera operando.
3 La extensión .ggt ayuda a distinguir las herramientas de los bocetos que tienen la usual de GeoGebra .ggb.
Importación de Nuevas Herramientas
Tras haber guardado una herramienta, es sencillo tanto reutilizarla en futuras construcciones, importándola a toda nueva ventana, como recuperarla para emplearla en otro equipo de destino. Basta con...
1 En la nueva ventana, si la nueva herramienta no apareciera, recurrir al ![]() Abre... del Menú Archivo y seleccionar el archivo ggt del directorio en que se hubiera guardado.
Abre... del Menú Archivo y seleccionar el archivo ggt del directorio en que se hubiera guardado.
2 Al pulsar el botón Abre, una vez seleccionado el archivo correspondiente a la herramienta requerida, se pasa a importarla para tenerla disponible en la ventana de trabajo como una más de la barra.
Protocolos de Desafíos de Construcción
A partir de las propuestas previas, se podría presentar un desafío para volver a instrumentarse no solo con el Teorema de Pitágoras sino también con lo recientemente explorado en relación al ángulo subtendido al diámetro de la circunferencia.
¿Cómo harían para…
... establecer el centro de una circunferencia si se restringiera el uso de varias herramientas? Se vedan:
- la de
 Medio o Centro
Medio o Centro - la de
 Mediatriz o similares
Mediatriz o similares - y hasta, parcialmente la de
 Intersección que solo se puede emplear en una única oportunidad
Intersección que solo se puede emplear en una única oportunidad
Si se tratara de conseguirlo con un círculo de papel, bastaría con plegarlo adecuadamente para conseguirlo. Si se permitiera el acceso a todas las herramientas, sería posible:
- aplicar de modo directo la de
 Medio o Centro o
Medio o Centro o - encontrar diversas estrategias (como encontrar la intersección de sendas mediatrices a un par de cuerdas).
Pero... ¿cómo sortear las restricciones que el desafío impone? Una alternativa se resume en los siguientes pasos de construcción.
Pasos de Construcción
| 1 | Plantear una figura de análisis, anotando en la Barra de Entrada, la ecuación: x^2 + y^2 = 16 o x² + y² = 16². Nota: Para que la construcción cobre mayor dinamismo, conviene trazar un segmento que podría denominarse como d_c de modo que la ecuación pasara a ser: x² + y² = d_c²
| |
| 2 | Crear un segmento de cuerda uniendo dos puntos sobre la circunferencia c. | |
| 3 | Trazar la perpendicular a la cuerda por uno de sus extremos, ubicado sobre la circunferencia. | |
| 4 | Establecer el punto de intersección entre la perpendicular y la circunferencia | |
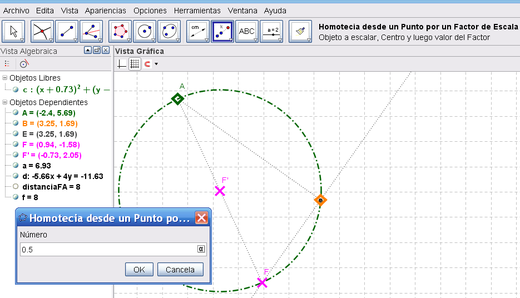
| 5 | Elegir una de las herramientas de transformación: la homotecia y con un clic sobre el punto de intersección y el extremo opuesta de la cuerda, ingresar 0.5 ó 1 / 2 en la caja de diálogo emergente para obtener el centro buscado |
Tarea para Protocolizar
Para pasarse la receta basta con:
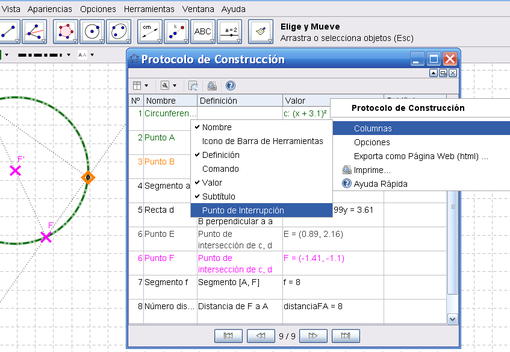
- Exponer la tarea paso a paso, lo que se consigue, sea exponiendo, desde el Menú Vista la Barra de Navegación (para que aparezca al pie de la Vista Gráfica, empleándola para ir desplegando el procedimiento en la Vista Gráfica) y/o el Protocolo de Construcción
- establecer algunos puntos de irrupción (también llamados de interrupción) para agrupar varios pasos (para lo que es preciso mostrar la correspondiente columna)
- indicar que se van a mostrar Solo los puntos de Irrupción
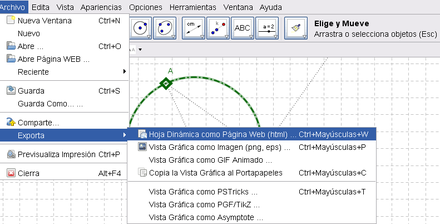
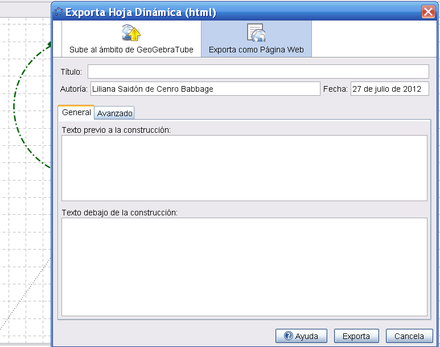
- Exportar la construcción como hoja dinámica, incluyendo la Barra de Navegación (Caja de Diálogo de Exporta – pestaña Avanzado) y guardar el archivo con un nombre ilustrativo como Centro_Circular_Restringido.html, por ejemplo.
- Abrir la hoja de trabajo dinámica exportada y empleando la Barra de Navegación repasar y revisar cada paso tomando nota de las herramientas empleadas.
Planteo
Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del ![]() Polígono regular?
Polígono regular?
En este tutorial, se compara el cuadrado que puede crearse con la ![]() Polígono regular con el de una
Polígono regular con el de una ![]() Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
1 Seleccionar una adecuada del Menú Apariencias y activar la Barra de Estilo en la Vista Gráfica para completar los preparativos.
Preparativos
Ocultar los ejes coordenados, exponer la cuadrícula y optar por la alternativa con la que se Ajusta a Cuadrícula' en la Barra de Estilo.
Paso a Paso
2 Marcar dos ![]() puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
3 Trazar...
- el [[File:Tool Midpoint or Center.gif]|link=Comentarios:Herramienta_de_Punto_Medio_o_Centro] punto medio y la
 mediatriz entre estos puntos
mediatriz entre estos puntos - la
 circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos. - los
 puntos de intersección entre la mediatriz y la circunferencia
puntos de intersección entre la mediatriz y la circunferencia - la
 semicricunferencia que se extiende entre uno y otro punto de intersección
semicricunferencia que se extiende entre uno y otro punto de intersección - un
 punto sobre esta semicircunferencia
punto sobre esta semicircunferencia - el punto que
 refleja en el punto medio entre los extremos, el recién marcado sobre la semicircunferencia
refleja en el punto medio entre los extremos, el recién marcado sobre la semicircunferencia - las
 rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semicircunferencia y el reflejado respectivamente.
rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semicircunferencia y el reflejado respectivamente.
4 Construir el polígono que tiene como vértices:
- el punto sobre la semicircunferencia,
- uno de los extremos de la diagonal del cuadrado en marcha,
- el punto reflejado,
- el otro extremo de la diagonal
5 Desplazar el punto que se trazó sobre la semicircunferencia hasta que ocupe la posición en que parece un cuadrado.
Justificaciones y Controles
El boceto se traza de modo tal que el punto que se desplaza sobre la semicircunferencia, su reflejado y los contiguos - vértices de la diagonal - conformen...
- un rectángulo
- que deviene cuadrado cuando se lo lleva hasta uno de los de intersección - ambos son extremos del recorrido por el que hasta se lo podría animar.
Conviene controlar...
- de modo más certero este comportamiento, empleando las herramientas adecuadas para contar con información sobre valores y relaciones
- las argumentaciones respecto a las vinculaciones entre el resultado de los ensayos y lo que la construcción desencadena en todos los casos.
Un Quehacer a Proyectar y Compartir
Pese a que lo más evidente - desde la óptica docente - es que la primera de las actividades depende directamente del empleo de herramientas con las que es preciso familiarizarse, ambas se entrecruzan con operaciones sobre la construcción dinámica:
- en exploraciones - guiadas por un propósito - que van dando entidad a...
- justificaciones causales de los efectos de ciertas maniobras - ¿es rectángulo? - ¿siempre? - ¿cómo hacemos para asegurarlo? - ¿cuándo parece pasar a cuadrado? - ....
- las relaciones entre los elementos que es preciso develar para respaldar la cadena de causalidades
- las correlaciones entre efectos, trazado y propiedades en juego que requieren un estudio conceptual
- ... de hecho, es la necesidad de validar estas presunciones lo que da razón de ser a su estudio.
Este recorrido expone un modelo de quehacer matemático que, escasamente transitado en términos generales frente a los estudiantes y con ellos, permite proyectarlo como medio de formación que puede completarse en intercambios virtuales.
Herramientas para el Control de Ensayos y Presunciones
6 Emplear las herramientas necesarias para controlar qué tipo de cuadrilátero se ha construido. Por ejemplo:
- la que traza y mide sus
 ángulos para corroborar que, tal como parece, son rectos
ángulos para corroborar que, tal como parece, son rectos - la que
 mide la longitud de cada lado
mide la longitud de cada lado - la que informa sobre la
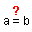 relación entre los segmentos de los lados y de las correspondientes rectas.
relación entre los segmentos de los lados y de las correspondientes rectas.
7 Procurar descripciones argumentadas sobre el tipo de cuadrilátero que se establece a medida que se desplaza el punto sobre la semicircunferencia.
Herramientas Propias para Completar las Disponibles
8 - Opción más Avanzada Dirigirse al manual para conocer la serie de pasos a partir de los cuáles, seleccionando el cuadrilátero creado como objeto de salida en la Nueva herramienta de la opción Creación de Herramienta Nueva del Menú de Herramientas, se puede crear la propia.
- En este caso, la que traza rectángulos (que pueden establecerse como cuadrados), dada su diagonal, como ilustra la siguiente figura.
- Habría que incluirlos en el listado correspondiente, si además del cuadrilátero (polígono), se deseara que otros elementos se expusieran en la salida (como los puntos vértices adicionales a los dados, los segmentos de lado, las rectas que los contienen, la semicircunferencia por la que se desplaza uno de los puntos de entrada, etc.).
- Una vez creada la herramienta, es posible cambiar el ícono que la acompaña así como otros detalles - nombre, ayuda -.
Planteo
Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del ![]() Polígono regular?
Polígono regular?
En este tutorial, se compara el cuadrado que puede crearse con la ![]() Polígono regular con el de una
Polígono regular con el de una ![]() Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
1 Seleccionar una adecuada del Menú Apariencias y activar la Barra de Estilo en la Vista Gráfica para completar los preparativos.
Preparativos
Ocultar los ejes coordenados, exponer la cuadrícula y optar por la alternativa con la que se Ajusta a Cuadrícula' en la Barra de Estilo.
Paso a Paso
2 Marcar dos ![]() puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
3 Trazar...
- el
 punto medio y la
punto medio y la  mediatriz entre estos puntos
mediatriz entre estos puntos - la
 circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos. - los
 puntos de intersección entre la mediatriz y la circunferencia
puntos de intersección entre la mediatriz y la circunferencia - la
 semicricunferencia que se extiende entre uno y otro punto de intersección
semicricunferencia que se extiende entre uno y otro punto de intersección - un
 punto sobre esta semicircunferencia
punto sobre esta semicircunferencia - el punto que
 refleja en el punto medio entre los extremos, el recién marcado sobre la semicircunferencia
refleja en el punto medio entre los extremos, el recién marcado sobre la semicircunferencia - las
 rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semicircunferencia y el reflejado respectivamente.
rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semicircunferencia y el reflejado respectivamente.
4 Construir el polígono que tiene como vértices:
- el punto sobre la semicircunferencia,
- uno de los extremos de la diagonal del cuadrado en marcha,
- el punto reflejado,
- el otro extremo de la diagonal
5 Desplazar el punto que se trazó sobre la semicircunferencia hasta que ocupe la posición en que parece un cuadrado.
Justificaciones y Controles
El boceto se traza de modo tal que el punto que se desplaza sobre la semicircunferencia, su reflejado y los contiguos - vértices de la diagonal - conformen...
- un rectángulo
- que deviene cuadrado cuando se lo lleva hasta uno de los de intersección - ambos son extremos del recorrido por el que hasta se lo podría animar.
Conviene controlar...
- de modo más certero este comportamiento, empleando las herramientas adecuadas para contar con información sobre valores y relaciones
- las argumentaciones respecto a las vinculaciones entre el resultado de los ensayos y lo que la construcción desencadena en todos los casos.
Un Quehacer a Proyectar y Compartir
Pese a que lo más evidente - desde la óptica docente - es que la primera de las actividades depende directamente del empleo de herramientas con las que es preciso familiarizarse, ambas se entrecruzan con operaciones sobre la construcción dinámica:
- en exploraciones - guiadas por un propósito - que van dando entidad a...
- justificaciones causales de los efectos de ciertas maniobras - ¿es rectángulo? - ¿siempre? - ¿cómo hacemos para asegurarlo? - ¿cuándo parece pasar a cuadrado? - ....
- las relaciones entre los elementos que es preciso develar para respaldar la cadena de causalidades
- las correlaciones entre efectos, trazado y propiedades en juego que requieren un estudio conceptual
- ... de hecho, es la necesidad de validar estas presunciones lo que da razón de ser a su estudio.
Este recorrido expone un modelo de quehacer matemático que, escasamente transitado en términos generales frente a los estudiantes y con ellos, permite proyectarlo como medio de formación que puede completarse en intercambios virtuales.
Herramientas para el Control de Ensayos y Presunciones
6 Emplear las herramientas necesarias para controlar qué tipo de cuadrilátero se ha construido. Por ejemplo:
- la que traza y mide sus
 ángulos para corroborar que, tal como parece, son rectos
ángulos para corroborar que, tal como parece, son rectos - la que
 mide la longitud de cada lado
mide la longitud de cada lado - la que informa sobre la
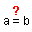 relación entre los segmentos de los lados y de las correspondientes rectas.
relación entre los segmentos de los lados y de las correspondientes rectas.
7 Procurar descripciones argumentadas sobre el tipo de cuadrilátero que se establece a medida que se desplaza el punto sobre la semicircunferencia.
Desafíos de Redescrubrimientos a la Euler
Propuesta y Desafío
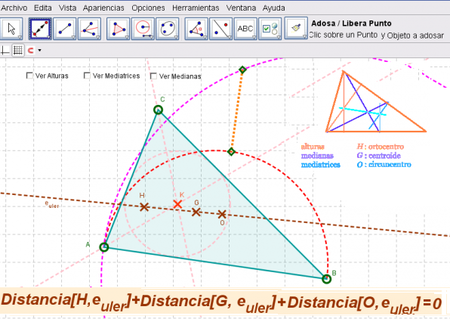
El desafío es indagar en qué condiciones se registra que el punto de intersección de dos de las bisectrices del triángulo queda ubicado sobre la recta de Euler. Se recomienda preparar cada una de las herramientas necesarias para trazar los puntos notables del triángulo que están sobre la recta de Euler.
Sobre el Escenarios del Desafío
- Plantear el escenario del desafío de manera completa.
- Proponer a los destinatarios que pases a explorarlo.
- Recomendar que, tal como se ilustra en la figura, de ser preciso se apele a la
 Herramienta de Punto (des)vinculado para ubicar el vértice C del triángulo en uno de los tramos punteados, como modo de establecer las relaciones propias de cada tipo de triángulo.
Herramienta de Punto (des)vinculado para ubicar el vértice C del triángulo en uno de los tramos punteados, como modo de establecer las relaciones propias de cada tipo de triángulo.