Diferencia entre revisiones de «Tutorial:Entre Construcciones y Dibujos»

m (link) |
m (link) |
||
| Línea 23: | Línea 23: | ||
**cómo corregir los errores paso a paso {{OJo|1= Los botones para [[File:Menu Undo.png]] [[Menú Edita#Deshace|Deshacer]] y [[File:Menu Redo.png]] [[Menú Edita#Rehace|Rehacer]] ofrecen un maniobrar más ágil que las correspondientes opciones del [[Menú Edita]]}}. | **cómo corregir los errores paso a paso {{OJo|1= Los botones para [[File:Menu Undo.png]] [[Menú Edita#Deshace|Deshacer]] y [[File:Menu Redo.png]] [[Menú Edita#Rehace|Rehacer]] ofrecen un maniobrar más ágil que las correspondientes opciones del [[Menú Edita]]}}. | ||
*Además... | *Además... | ||
| − | **cómo abrir una [[File:Menu New.png]] [[ | + | **cómo abrir una [[File:Menu New.png]] [[Comentarios:Menúes#Nueva Ventana|Nueva Ventana]] de GeoGebra con esa opción del [[Comentarios:Menúes|Menú Archivo]] y/o ver el [[Menú de Ventana#Lista de Ventanas Abiertas de GeoGebra|Lista de Ventanas Abiertas de GeoGebra]] y/o iniciar un [[Comentarios:Menúes#Nuevo|nuevo boceto]]. |
**cómo crear nuevos puntos "sobre la marcha, con las diversas herramientas que lo permiten y, por lo tanto, no requieren se su previa existencia. {{example|1= La [[File:Tool Segment between Two Points.gif]] [[Herramienta de Segmento]] puede ''aplicarse'' a dos puntos ya existentes o dar lugar, con cada oportuno ''clic'' en posiciones vacías de una u otra [[Vista Gráfica]], a su trazado.}} | **cómo crear nuevos puntos "sobre la marcha, con las diversas herramientas que lo permiten y, por lo tanto, no requieren se su previa existencia. {{example|1= La [[File:Tool Segment between Two Points.gif]] [[Herramienta de Segmento]] puede ''aplicarse'' a dos puntos ya existentes o dar lugar, con cada oportuno ''clic'' en posiciones vacías de una u otra [[Vista Gráfica]], a su trazado.}} | ||
*Particularmente, cómo ''activar'' cada una de las siguientes [[File:Tool.png]] [[Comentarios:Núm_HerramientasES|Herramientas]] | *Particularmente, cómo ''activar'' cada una de las siguientes [[File:Tool.png]] [[Comentarios:Núm_HerramientasES|Herramientas]] | ||
| Línea 36: | Línea 36: | ||
**enfocar con un [[File:Tool Zoom In.gif]] [[Herramienta de Aproximar|Acerca]] / [[File:Tool Zoom Out.gif]] [[Herramienta de Alejar|Aleja]] | **enfocar con un [[File:Tool Zoom In.gif]] [[Herramienta de Aproximar|Acerca]] / [[File:Tool Zoom Out.gif]] [[Herramienta de Alejar|Aleja]] | ||
*Recordar el modo en que se opera para... | *Recordar el modo en que se opera para... | ||
| − | **[[File:Menu Save.png]] [[ | + | **[[File:Menu Save.png]] [[Comentarios:Menúes#Guarda|Guardar archivos]] de GeoGebra |
| − | **[[File:Menu Open.png]] [[ | + | **[[File:Menu Open.png]] [[Comentarios:Menúes#Abre...|Abrir un archivo]] de GeoGebra ya existente |
=== Construcción de un Marco ¿Rectangular?=== | === Construcción de un Marco ¿Rectangular?=== | ||
Revisión del 08:07 27 mar 2020
Planteo
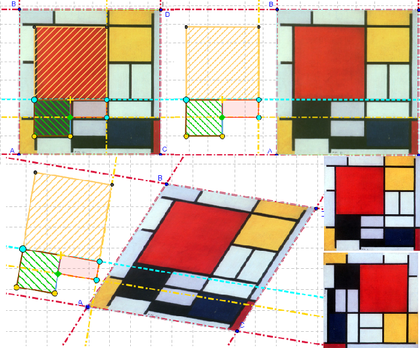
¿Cómo asociar, relacionar y distinguir meros dibujos de construcciones a partir de una obra claramente geométrica de Mondrian?
Preparativos
Para preparar el ambiente de trabajo, se empieza por:
- Seleccionar del Menú Apariencias, las más adecuada . Por ejemplo, Geometría .
- Emplear la
 Herramienta de Imagen para insertar el retazo de la obra de Mondrian que aparece a continuación.
Herramienta de Imagen para insertar el retazo de la obra de Mondrian que aparece a continuación.
- Distribuir las consignas que se prefieran de las que se ofrecen a continuación (u otras que surgieran de la imaginación de los participantes siempre que el desafió esté operativamente a su alcance)
- Consignas Posibles:
- Emplear el
 Lápiz para señalar con diferentes colores los dibujos que parezcan tener forma cuadrada, rectangular u otras. Procurar alguna maniobra para controlar el grado de ajuste a cada apreciación.
Lápiz para señalar con diferentes colores los dibujos que parezcan tener forma cuadrada, rectangular u otras. Procurar alguna maniobra para controlar el grado de ajuste a cada apreciación. - Marcar puntos para las tres esquinas del dibujo que se inserta y establecer el cuarto de modo tal que al arrastrar cualquiera de los tres primeros, el marco creado siga encuadrando adecuada y dinámicamente.
- Crear un polígono cualquiera y en lugar de colorearlo seleccionar una imagen como relleno y ver cómo reacciona al arrastrar los vértices del polígono.
- Intentar el calco de alguna de las secciones del dibujo y contrastar la construcción con el modelo.
- Emplear el
- Consignas Posibles:
- Resumir el modo de emplear las herramientas y las maniobras básicas con las que se requiere ganar familiaridad. Sintetizando, por ejemplo:
- Cómo seleccionar un objeto ya existente.
 Atención: Cuando el puntero de selección apunta a un objeto, cambia su forma - de cruz a flecha- y un clic oportuno lo selecciona.
Atención: Cuando el puntero de selección apunta a un objeto, cambia su forma - de cruz a flecha- y un clic oportuno lo selecciona.
- Cómo seleccionar un objeto ya existente.
- Así cómo...
- crear un punto en un objeto.
 Atención: Un punto sobre un objeto no tiene el color azul que identifica a los libres ni el negro característico de los dependientes fijos (como los de intersección, por ejemplo. Son celestes y al intentar
Atención: Un punto sobre un objeto no tiene el color azul que identifica a los libres ni el negro característico de los dependientes fijos (como los de intersección, por ejemplo. Son celestes y al intentar  arrastrarlos con el ratón o mouse, solo recorren el circuito o zona del objeto sobre el que fueron creados con la
arrastrarlos con el ratón o mouse, solo recorren el circuito o zona del objeto sobre el que fueron creados con la  herramienta correspondiente.
herramienta correspondiente.
- crear un punto en un objeto.
- Incluso...
- cómo corregir los errores paso a paso
 Atención: Los botones para
Atención: Los botones para  Deshacer y
Deshacer y  Rehacer ofrecen un maniobrar más ágil que las correspondientes opciones del Menú Edita
Rehacer ofrecen un maniobrar más ágil que las correspondientes opciones del Menú Edita
- cómo corregir los errores paso a paso
.
- Además...
- cómo abrir una
 Nueva Ventana de GeoGebra con esa opción del Menú Archivo y/o ver el Lista de Ventanas Abiertas de GeoGebra y/o iniciar un nuevo boceto.
Nueva Ventana de GeoGebra con esa opción del Menú Archivo y/o ver el Lista de Ventanas Abiertas de GeoGebra y/o iniciar un nuevo boceto. - cómo crear nuevos puntos "sobre la marcha, con las diversas herramientas que lo permiten y, por lo tanto, no requieren se su previa existencia. Ejemplo: La
 Herramienta de Segmento puede aplicarse a dos puntos ya existentes o dar lugar, con cada oportuno clic en posiciones vacías de una u otra Vista Gráfica, a su trazado.
Herramienta de Segmento puede aplicarse a dos puntos ya existentes o dar lugar, con cada oportuno clic en posiciones vacías de una u otra Vista Gráfica, a su trazado.
- cómo abrir una
- Particularmente, cómo activar cada una de las siguientes
 Herramientas
Herramientas
 Punto y
Punto y  Punto en Objeto
Punto en Objeto Elige y Mueve
Elige y Mueve Recta y
Recta y  Segmento
Segmento- la de
 Polígono y de las de polígonos, también la de
Polígono y de las de polígonos, también la de  Polígono regular.
Polígono regular.  Lápiz
Lápiz
- Así como las que permiten...
 Eliminar
Eliminar Desplazar la Vista Gráfica
Desplazar la Vista Gráfica- enfocar con un
 Acerca /
Acerca /  Aleja
Aleja
- Recordar el modo en que se opera para...
 Guardar archivos de GeoGebra
Guardar archivos de GeoGebra Abrir un archivo de GeoGebra ya existente
Abrir un archivo de GeoGebra ya existente
Construcción de un Marco ¿Rectangular?
Por empezar, además de los preparativos, se pasa a...
- activar la Barra de Estilo, exponer la Cuadrícula y indicar la alternativa por la que cada elemento se Ajusta a Cuadrícula
- con la herramienta correspondiente, insertar
 la figura con la que se va a organizar la producción de dibujos y construcciones.
la figura con la que se va a organizar la producción de dibujos y construcciones. - con la opción
 correspondiente del Menú Contextual, renombrarla Mondrian - apellido de su autor -
correspondiente del Menú Contextual, renombrarla Mondrian - apellido de su autor -
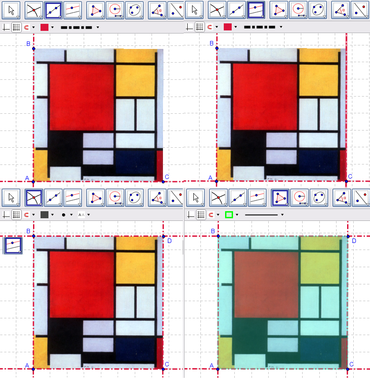
 ubicar el dibujo en una posición adecuada de la Vista Gráfica y tres
ubicar el dibujo en una posición adecuada de la Vista Gráfica y tres  puntos en las esquinas inferiores y la superior izquierda, como se observa en la figura.
puntos en las esquinas inferiores y la superior izquierda, como se observa en la figura.- con un clic derecho sobre la imagen apuntada
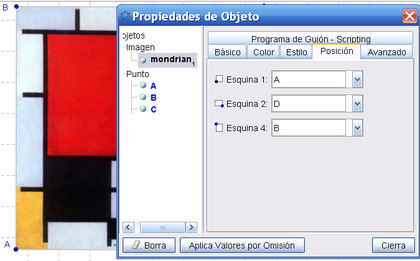
 , en el desplegado Menú Contextual, seleccionar la opción de Propiedades para pasar a la pestaña correspondiente de la Caja de Diálogo y determinar los puntos de cada esquina del marco como se ilustra en la figura.
, en el desplegado Menú Contextual, seleccionar la opción de Propiedades para pasar a la pestaña correspondiente de la Caja de Diálogo y determinar los puntos de cada esquina del marco como se ilustra en la figura.
- aceptar las determinaciones en cuanto a las esquinas para volver a la Vista Gráfica
- para darle un marco al cuadro, trazar:
- las
 rectas que pasan por A y B y B y C respectivamente
rectas que pasan por A y B y B y C respectivamente - las
 paralelas a cada recta recién creada que pasan por A y por C respectivamente
paralelas a cada recta recién creada que pasan por A y por C respectivamente - el
 punto de intersección entre sendas paralelas
punto de intersección entre sendas paralelas - creando el
 polígono que une B con este punto de intersección, con A y con C, cerrándolo con un reiterado clic sobre B
polígono que une B con este punto de intersección, con A y con C, cerrándolo con un reiterado clic sobre B
- las
- revisar los pasos como para notar qué tipo de encuadre se le dió al dibujo.
Estar entre ser y parecer
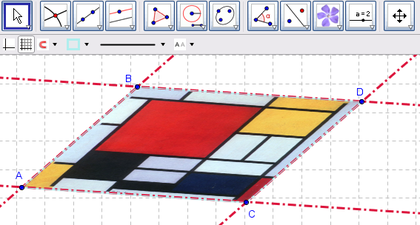
Lo que aparenta ser un encuadre rectangular (incluso, cuadrado) del dibujo, demuestra que no es lo que parece con solo someterlo a la prueba de arrastre -del punto B a izquierda y derecha, arriba y a abajo, por ejemplo- y notar los efectos de cada maniobra.
Es un momento adecuado para preguntarse cómo se hubiera comportado el marco creado si en lugar de operar con ![]() rectas paralelas para dar con el cuarto vértice, se hubiera recurrido a
rectas paralelas para dar con el cuarto vértice, se hubiera recurrido a ![]() perpendiculares.
perpendiculares.
Acaso convenga redefinir las rectas que dieron lugar D de ese modo y controlar los cambios de efectos así como establecer explicaciones al respecto.
¿Calcando Dibujos?
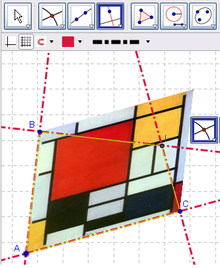
Para procurar un calco de al menos algunos componentes del dibujo - los que parecen cuadrados, el central y el que aparece debajo así como el que se aprecia rectangular, adosado a uno y otro - se siguen los pasos indicados en el siguiente recorte de Protocolo de Construcción.
Si al terminar se desplaza el dibujo hacia la derecha, quedan a la izquierda las construcciones calcadas que, pese a los esfuerzos de copistas, no se comportan con la misma facilidad de adaptación a los arrastres que el marco y el dibujo.
Al interrogarse sobre las diferencias, surge las que distinguen las construcciones que se basan en cierto juego de relaciones y propiedades que vinculan a los elementos en juego de las que meramente los trazan sin asociarlos dinámicamente - o lo hacen desde otras condiciones como en el caso de las paralelas en lugar de las perpendiculares y viceversa-.
Analizando el Protocolo de Construcción
Si se analizan cuidadosamente los pasos que se presentan en el siguiente Protocolo - el obtenido a partir de las maniobras de construcción - se pueden distinguir las producciones de genuinos rectángulos de las de apenas paralelogramos, de las de cuadrados de las de meros contornos.
Básicos de Centro Babbage - IG-ArgentinaLiliana Saidon -Hoy
Entrada desde el Álgebra
Dando Entrada a Objetos de Definición Algebraica
1 . Se les da Nombre a Nuevos Objetos, simplemente anteponiendo su nombre = en la Barra de Entrada a su definición algebraica.
2 . Un Producto se establece con un asterisco o espacio entre los factores.
3 . ¡GeoGebra es sensible a las minúsculas diferencias!... lo que implica que identifica como distintos los nombres de variables en que solo una mayúscula o un tilde distingue una de otra. Por eso es preciso controlar estas cuestiones tanto al otorgar un nombre como al referirlo.
- Los nombres que otorga GeoGebra, espontáneamente a los objetos creados - sea a partir de una herramienta como desde un comando - presentan ciertas distinciones y así, los de los...
- Puntos son letras mayúsculas. Ejemplo: A = (1, 2) o, en coordenadas polares, B = (2; pi)
- Vectores son letras minúsculas Ejemplo: v = (1, 3)
 Atención: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
Atención: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
- Puntos son letras mayúsculas.
- Llevan minúsculas también las...
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados Ejemplo: circunferencia c: (x – 2)^2 + (y – 1)^2 = 16
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados
- Deben anotarse y referirse en minúsculas los nombres de las variables como...
- la independiente x de una función o
- x e yen cualquier expresión - ecuación de una sección cónica, de una inecuación, etc. -. Ejemplo: f(x) = 3*x + 2
4 . Para incluir un objeto en una anotación en la Barra de Entrada, es preciso crearlo antes y referirlo por el nombre que lo identifica, recordando distinguirlo con todos los detalles correspondientes (mayúsculas, minúsculas, tildes...). Esto vale tanto para las expresiones algebraicas como para los comandos...
- y = m x + b o y = m f(-b) x + f(b) crea una recta en tanto m como b sean ya:
- números que harán las veces de parámetros (recordar que todo número establecido como tal involucra un deslizador cuyo valor puede modificarse en tanto se lo torne visible en la Vista Gráfica activa.
- Recta(A, B) o Recta(A + b Vector(A, B), B) crea una recta en tanto exista el punto A y el B y/o el número b.
5 . Cada expresión ingresada en la Barra de Entrada se debe confirmar' pulsando la tecla Enter (o Intro como aparece en algunos teclados).
6 . Tanto la tecla de atajo (F1) como la opción de Ayuda del Menú o el Manual, permiten abrir la ventana pertinente para averiguar el modo de empleo de un comando en la Barra de Entrada.
7 . Si al ingresar un comando en la Barra de Entrada aparece un error, conviene leer detenidamente el correspondiente mensaje para tener mayores recursos para subsanarlo.
8 . Los Comandos se pueden anotar o seleccionar desde la lista próxima a la Barra de Entrada.
9 . Tras anotar las dos primeras letras de cualquier comando en la Barra de Entrada, emergen alternativas para su Completado Automático tentativo que permite...
- Seleccionar el adecuado pulsando Enter ( Intro en algunos teclados) para ubicar el cursor entre los corchetes.
- Proseguir anotando las siguientes letras hasta que se despliegue el deseado.
Construyendo Circunferencias Suponiendo sus Tangentes
¿Por qué no realizar el trayecto de regreso desde las construcciones convencionales imaginando un desafío inverso en que se pueda tantear dinámicamente como medio legítimo para dar con conjeturas a controlar y validar? Imaginemos que la consigna fuese la siguiente:
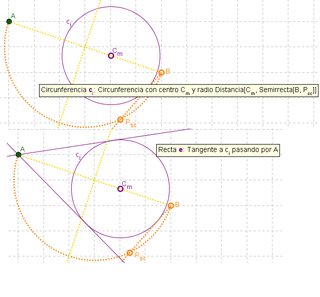
- Dicen que había una circunferencia a la que se le trazaron las tangentes desde los puntos A y B - que es todo lo que ha perdurado de esa antiquísima construcción ya desvaída - y algunos creen recordar que esas cuatro tangentes conformaban un específico cuadrilátero. El desafío es establecer qué tipo de cuadrilátero podría haber sido, más allá de las que nos proponen los rumores de los que se consideran dignos memoriosos, así como descartar los que no tendrían chance alguna de haber sido.
Desafío guiando el Tutorial
Rastros para una Construcción Retrospectiva
Especulaciones hacia y desde la Figura de Análisis
Consideraciones Iniciales
- Algunos aseguran que sin necesidad de reconstruir lo que ese diagrama podría haber configurado, pueden descartarse algunos cuadriláteros desde ya y señalan, por ejemplo, la imposibilidad de...
- todo trapecio
- los rectángulo en general
- los rombos en particular
- Otros sostienen que no es dable descartar ninguno de entrada y que es conveniente comenzar por una figura de análisis retrospectivo para empezar. Valdría cuestionarse si...
- ¿Se puede justificar una u otra posición?
Reconsiderando sobre la Figura de Análisis
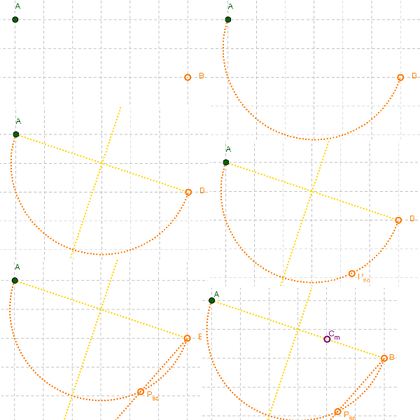
- En la construcción, los puntos A y B establecen los datos dados y deben permanecer fijos.
- Sobre la construcción realizada siguiendo el tutorial, se puede modificar la posición del centro de la presunta circunferencia y la del punto que, sobre la semicircunferencia entre A y B, establece la dirección de la primera de las tangentes.
- Este interjuego de resultados de los desplazamientos de esos dos puntos deslizables ofrece un banco de pruebas dinámico.
- La exploración se limita a desplazar el punto C_m (que opera como centro de la presunta circunferencia que se intenta reconstruir) y el P_{sc} que, sobre la semicircunferencia desde A a B, determina el sentido de la primera tangente.
- A partir de los ensayos, se podría reconsiderar si...
- El tanteo sistemático, ¿permite distinguir lo que efectivamente se pudiera descartar de entrada de lo que no puede determinarse a menos que se brinden más datos?
- ¿Qué herramientas podrían emplearse alternativamente para recrear la construcción?
- ¿Con qué medios puede controlarse si el cuadrilátero delimitado por las cuatro presuntas tangentes constituyen uno de algún tipo específico?
- ¿Se evidencian relaciones entre los elementos que se distinguen como propiedades exclusivas de un tipo de cuadrilátero?
- Si el punto que opera como presunto centro de la circunferencia reconstruida se desplaza convenientemente, ¿se obtienen distintos cuadriláteros sin necesidad de modificar la posición del que se emplea para tantear la dirección de la primera de las tangentes?
- ¿Es posible establecer el tipo de cuadriláteros imposibles de configurar dadas las condiciones o es la construcción seleccionada la que restringe y aparenta la inviabilidad de lo que en otra podrían lograrse?
- Si se partiera de otro tipo de construcción, ¿será posible dar con otro tipo de cuadriláteros que en la planteada no parecen ser viables?
Comandando la Construcción
Definiciones en el Protocolo de Construcción
Si bien el tutorial parece estar basado exclusivamente en las herramientas disponibles, podría haber sido desarrollado sin siquiera apelar al ratón o mouse y / o cualquier dispositivo de contacto dado que se podrían preparar todos los archivos de GeoGebra ingresando los datos respecto de los objetos y anotando los correspondientes comandos en la Barra de Entrada.
El ingreso de datos algebraicos y de comandos supera y amplia el empleo de las herramientas geométricas.
Pruebas y Preparativos
- Abrir una nueva ventana de GeoGebra.
- Exponer la Vista Algebraica y la Barra de Entrada así como la cuadrícula (sea desde el Menú Vista o apelando a los íconos de cada Barra de Estilo según corresponda).
- Seguir paso a paso las indicaciones del Protocolo de Construcción intentando intercalar el empleo de herramientas y el ingreso de los comandos correspondientes en la Barra de Entrada.
| Para modificar la definición de un objeto, basta con seleccionarlo con la herramienta Al terminar, es preciso pulsar la tecla Enter (Intro en algunos teclados). |
Basta con seleccionarlo con la herramienta
Controlar y Explorar la Construcción
- Controlar que los únicos puntos que se pueden desplazar (además de A y B que son datos dados y no debieran moverse como no sea para cambiar las condiciones iniciales), sean los que determinan el centro de la presunta circunferencia y el que, sobre la semicircunferencia, fija el sentido de la primera tangente tentativa.
- Someter la construcción a la prueba de arrastre para verificar que si bien se modifica, las relaciones que se establecieron no se alteran y el rol de los elementos en juego perdura correctamente.
- Cambiar las propiedades de los objetos para ilustrar mejor las relaciones y distinguir los elementos claves así como para mejorar la apariencia de la construcción (por ejemplo, seleccionando los colores armoniosamente, distinguiendo con trazos punteados los elementos auxiliares ,…)
- Guardar la construcción que lleva a la resolución del desafío con un nombre adecuado.
Explorando Relaciones entre Coeficientes y Gráficas en Cuadráticas
En esta propuesta se procurará vincular en sentido directo e inverso, las relaciones entre los coeficientes de una expresión cuadrática y su comportamiento gráfico.
Desafío Reconstructivo
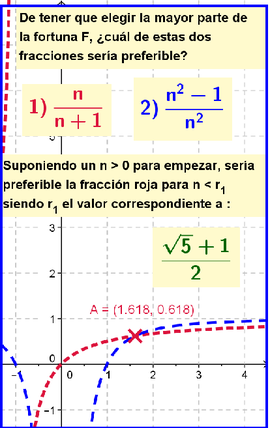
Dados cinco puntos distribuidos al azar, ¿cómo se podría deslizar la gráfica de y = x^2 usando las teclas flecha ascendentes / descendentes y las laterales a izquierda y derecha para que la gráfica cruce por la mayor cantidad de tales puntos?
Preparativos
1 Ingresar en la Barra de Entrada, cinco veces esta anotación para dar con puntos al azar: (-5 + round(10random()), -4 + round(10random()))
Recordar que con las teclas Alt + Arriba / Alt + Abajo se puede navegar por la historia de comandos ingresados.
Por lo tanto, basta con realizar la anotación una única vez y luego recuperar lo ingresado y volver a pulsar Enter (Intro en algunos teclados) para marcar los siguientes puntos.
- darle a cada uno vistoso y diverso formato y color
- pulsar las teclas Ctrl + R para que el recálculo de los valores aleatorios provoque una reubicación de los puntos en caso de no estar en una posición adecuada.
2 Ingresar en la Barra de Entrada la siguiente expresión: y = x^2
3 Seleccionar la expresión y...
- pulsar las teclas Arriba / Abajo u las Izquierda / Derecha
- registrar el efecto que estas maniobras tienen sobre el gráfico y la expresión correspondiente.
4 Establecer alguna estrategia para lograr que la cuadrática cruce por la mayor cantidad posible de puntos.
Sencillamente, se ingresa sucesivamente en la Barra de Entrada:
- los valores de partida para a, b y c - a = 1 - b=0 - c = 0 - y luego la expresión:
a x^2 + b x + c- - a la que se le puede otorgar un color y estilo que la distinga de la previamente ingresaday = x^2-
Se pasa a dar visibilidad a los números a, b y c con un clic en cada redondelito que aparece a la izquierda de cada uno de ellos en la Vista Algebraica. Es notorio, entonces que...
- cuando los números a, b y c se hacen visibles en la Vista Gráfica, quedan asociados a deslizadores
Tales deslizadores así originados, adoptan el rango de valores e incremento que tienen por omisión (de -5 a 5 con un incremento de 0.1) y el valor que se les otorgara al crearlos.
Pueden llevarse adelante algunos ensayos para corroborar que...
- la gráfica de la expresión ingresada - a x^2 + b x + c - reacciona a los cambios en los valores de los deslizadores.
En cambio...
- mantiene su carácter de objeto libre la que fuera originalmente anotada como y = x^2" y cambia su representación gráfica y expresión cuando se la selecciona y se opera con las teclas de flecha.
Planteando Alternativas
Incluso para problemas aparentemente sencillos, es interesante desplegar el planteo empleando las diversas vistas y alternativas que ofrece GeoGebra.
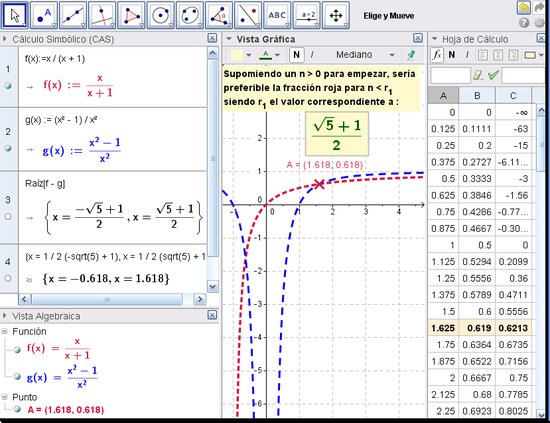
El siguiente es un desafío que se analiza tanto en la Vista Gráfica como en la Vista Algebraica, en la Vista CAS y en la Hoja de Cálculo:
Se establece el planteo, el análisis y la graficación empleando cada uno de los posibles registros, tal como se ilustra a continuación:
Escenarios de Análisis
Algunos efectos y detalles escasamente se reflejan en el Protocolo de Construcción. Como se aprecia en la siguiente aplicación de examen fluido de las funciones por tramos solicitada a por la profesora del segundo año del CET 18 (Escuela Técnica de Villa Regina en la Provincia de Río Negro de la Argentina), con la expectativa de motivar su análisis con un recurso interactivo en que obrara una retroalimentación visual con el empleo de los colores dinámicos.
Justamente porque esa era la modalidad requerida, las relaciones que debían establecerse quedarían integradas al diseño sin dejar evidencias en el Protocolo.
Esto implicó que la indagación del boceto se hiciera con un estilo de estudio de caja negra en que el surgimiento de rastros permitiera correlacionar entradas y salidas con características de la función y su régimen de variación.
Rastros en lugar de enunciaciones para devolver la tarea de puesta en palabra a los intérpretes de esos coloridos Indicadores que, surgidos en cada ensayo, pudieran borrarse tras cada intento, pulsando el botón Limpia Rastros. Así diseñado, este escenario dejó la responsabilidad de encontrar vínculos a los exploradores de segundo año que se hicieron cargo de la tarea con sorprendente ahínco.
Algunos Detalles
La llave representada por el ![]() Deslizador, permite pasar de una función por tramos a otra y el boceto está preparado para incorporar, en la lista correspondiente, funciones adicionales.
Deslizador, permite pasar de una función por tramos a otra y el boceto está preparado para incorporar, en la lista correspondiente, funciones adicionales.
El botón que LimpiaRastros es particularmente útil cuando se quiere empezar de nuevo, desde el principio y/o para revisar una zona específica.
| Es importante primero, limpiar lo previo para que no resulte confusa la superposición con los restos de rastros anteriores. |
.
Los anuncios en los cartelitos emergentes respecto de la cuesta, incluyendo el de "Amesetando la Cuesta", hacen referencia a la índole creciente, decreciente o de inflexión y se corresponden con los colores sobre la curva.
| Sobre la curva se ilustra y distingue en azul o rojo el signo de la curvatura, reservando el verde para las zonas que los cartelitos anuncian como de amesetamiento. |
Los colores sobre el eje x se corresponden con imagen positiva o negativa en una codificación colorida en relación al signo de la imagen y controla si la función está efectivamente definida o no.
Se podría cuestionar si la codificación respecto de la concavidad de la curva podría quedar habilitada o no añadiendo una ![]() casilla de control para que sea posible ir centrando la atención en una cuestión por vez.
casilla de control para que sea posible ir centrando la atención en una cuestión por vez.
| Acaso se podría decidir colocar una casilla de control para exponer o no cada evidencia y sus rastros como, por ejemplo: Punteado sobre EjeY Punteado sobre EjeX Punteado sobre la Curva |
Aparecen diversos detalles que vale descubrir explorando para, además, ir reencontrando su utilidad al ahondar en las indagaciones. Como, por ejemplo, la necesidad de emplear el botón LimpiaRastros entre uno y otro emprendimiento. Sea el de cambiar de sector de análisis, de función o de reinicio.
 Atención: La clave de este escenario es que permite...
Atención: La clave de este escenario es que permite...
- una interpretación de indicios evitando las enunciaciones
- enunciaciones que podrían implicar sobre-simbolizaciones
- sobre-simbolizaciones que pueden, además, omitir la necesidad de explorar y/o remitir a quienes lo recorren a una posición de recepción y hasta acatamiento en lugar de la de responsables de desentrañar el funcionamiento de la caja negra
- desentrañar con otros, durante la actividad que desencadena la situación que se propone con este diseño.
- una interpretación de indicios evitando las enunciaciones
Descripciones Vívidas
Acaso la mejor manera de describir este boceto sea a través del relato de la profesora Susana, que solicitó este boceto a trabajó en clase con sus estudiantes de media y que tuvo la gentileza de ir registrando que...
(...) las preguntas surgieron sobre la marcha, en la misma clase, quizá porque un primer intento guiado por un instructivo, podría haber circunscripto las reacciones.
Reacciones que, concluyó, desencadenaba una práctica intensa de un ritmo no alcanzado con la multiplicación de ejemplos en la pizarra muy demandantes de tiempo. Práctica que, en este caso, privilegiaba distinguir dado que...
Boceto que estaban explorando en un tácito análisis colorido de la función.
Así, con un boceto preliminar (continuo a trazos en el que no quedaba señalada la ordenada en el eje Y)...
Lo rescatable para la profesora parecía centrarse en que asumían ese quehacer matemático mejorando durante el desenvolvimiento, las estrategias para ir identificando indicios, y compartiéndolas con sus compañeros.
En tal sentido, la profesora distinguió algunas ventajas respecto de este medio diseñado para que el análisis surgiera sin los requerimientos de saberes previos que demanda la herramienta de ![]() Inspección de funciones con la que se planteaba trabajar en un segundo momento. Por ejemplo...
Inspección de funciones con la que se planteaba trabajar en un segundo momento. Por ejemplo...
Sus conclusiones avanzan más allá de los contenidos en juego, para darle entidad al cambio del contrato pedagógico durante la actividad propuesta...
un dato no menor
Enfatiza en lo que rescata cómo quedan identificadas las cuestiones más rápidamente y sin errores así como que se ahorra el tiempo, porque generalmente se tienen que presentar muchos ejemplos gráficos para que incorporen la lectura correcta de gráficos y, sobre todo, la dinámica a partir de la que los conceptos quedan claros aunque no sean formalmente enunciados. Es más fácil trabajar sobre el boceto y luego, acaso en una institucionalización compartida, formalizar los conceptos.
Las intervenciones que registra incluyen, más que las explicaciones, las preguntas
Añade, en una puesta en acto de lo que suele enunciarse como propio de la dialéctica herramienta-objeto que, sin depositar exclusivamente las expectativas en lo experimental...
Análisis a Posteriori
En un análisis a posteriori en el que se virtualmente dialoga con sus eventuales colegas, se detiene para hacer algunas consideraciones...
Deja también alguna atendible sugerencia para quienes diseñamos el boceto:
(...) Con respecto al boceto en sí, creo que no es necesario que se vaya marcando sobre el eje y la imagen de la función (que es lo que pedí para el segundo boceto y que no tenía el preliminar que me prepararon). Más que nada, porque queda marcado como un punto y puede confundir (la coordenada es un punto lo cual no es rigurosamente correcto). Aunque en mi experiencia, mis alumnos no tuvieron problema al respecto.
.
Esto, por una cuestión de consistencia, explica, ya que...
la indicación de moverse de izquierda a derecha, si se quisiera analizar todo el dominio de un dominio infinito a la izquierda, debiera obviarse porque haría necesario volver para atrás, lo que contradice la indicación del boceto.
Nos aclara que lo puntualiza...
Así, más allá de la gentileza de la solicitud, demuestra la profundidad de la reflexión sobre la práctica.
Reflexión en la que integra el diseño del medio y su articulación con la acción que espera se desencadene, observando la coherencia entre la organización disciplinar, didáctica e instrumental.
| Este diseño mancomunado en que desde el sur del sur propicia la profesora Susana, involucra recorridos en los que el diálogo va configurando medios con un desenvolvimiento que esperamos seguir recorriendo con entusiasmo colaborativo. |