Diferencia entre revisiones de «Tutorial:Diagonales Cuadradas»

m (link) |
|||
| Línea 1: | Línea 1: | ||
{{Tutorial | {{Tutorial | ||
|title=Diagonal de un Cuadrado <small>Basado en Diseño de un Taller de Centro Babbage</small> | |title=Diagonal de un Cuadrado <small>Basado en Diseño de un Taller de Centro Babbage</small> | ||
| − | }} | + | }}{{Interfaz Gráfica|Diagonales}} |
=== Planteo === | === Planteo === | ||
Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del [[File:Tool Regular Polygon.gif|24px]] [[Herramienta de Polígono regular|Polígono regular]]? | Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del [[File:Tool Regular Polygon.gif|24px]] [[Herramienta de Polígono regular|Polígono regular]]? | ||
| Línea 18: | Línea 18: | ||
*el [[File:Tool Midpoint or Center.gif]] [[Herramienta de Medio o Centro|punto medio]] y la [[File:Tool Perpendicular Bisector.gif]] [[Herramienta de Mediatriz|mediatriz]] entre estos puntos | *el [[File:Tool Midpoint or Center.gif]] [[Herramienta de Medio o Centro|punto medio]] y la [[File:Tool Perpendicular Bisector.gif]] [[Herramienta de Mediatriz|mediatriz]] entre estos puntos | ||
*la [[File:Tool Circle Center Point.gif]] [[Herramienta de Circunferencia (centro-punto)|circunferencia]] con centro en el punto medio recién establecido, que pasa por uno de los puntos. | *la [[File:Tool Circle Center Point.gif]] [[Herramienta de Circunferencia (centro-punto)|circunferencia]] con centro en el punto medio recién establecido, que pasa por uno de los puntos. | ||
| − | *los [[File:Tool Intersect Two Objects.gif]] [[ | + | *los [[File:Tool Intersect Two Objects.gif]] [[Referencia:Herramientas_3D_a_libro#Sobre_la_Intersección|puntos de intersección]] entre la mediatriz y la circunferencia |
*la [[File:Tool Semicircle through Two Points.gif]] [[Herramienta de Semicircunferencia|semicricunferencia]] que se extiende entre uno y otro punto de intersección | *la [[File:Tool Semicircle through Two Points.gif]] [[Herramienta de Semicircunferencia|semicricunferencia]] que se extiende entre uno y otro punto de intersección | ||
*un [[File:Mode point.png]] [[Herramienta de Punto|punto]] sobre esta semicircunferencia | *un [[File:Mode point.png]] [[Herramienta de Punto|punto]] sobre esta semicircunferencia | ||
Revisión del 23:05 14 feb 2020
Planteo
Problema: ¿Cómo hacerle ganar versatilidad al cuadrado del ![]() Polígono regular?
Polígono regular?
En este tutorial, se compara el cuadrado que puede crearse con la ![]() Polígono regular con el de una
Polígono regular con el de una ![]() Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
Herramienta Personal que se puede preparar para la construcción de cuadrados dada la longitud - no ya de su lado - sino de su diagonal.
1 Seleccionar una adecuada del Menú Apariencias y activar la Barra de Estilo en la Vista Gráfica para completar los preparativos.
Preparativos
Ocultar los ejes coordenados, exponer la cuadrícula y optar por la alternativa con la que se Ajusta a Cuadrícula' en la Barra de Estilo.
Paso a Paso
2 Marcar dos ![]() puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
puntos que harán las veces de extremos del segmento diagonal del cuadrado en marcha..
3 Trazar...
- el
 punto medio y la
punto medio y la  mediatriz entre estos puntos
mediatriz entre estos puntos - la
 circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos.
circunferencia con centro en el punto medio recién establecido, que pasa por uno de los puntos. - los
 puntos de intersección entre la mediatriz y la circunferencia
puntos de intersección entre la mediatriz y la circunferencia - la
 semicricunferencia que se extiende entre uno y otro punto de intersección
semicricunferencia que se extiende entre uno y otro punto de intersección - un
 punto sobre esta semicircunferencia
punto sobre esta semicircunferencia - el punto que
 refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia
refleja en el punto medio entre los extremos, el recién marcado sobre la semi-circunferencia - las
 rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente.
rectas que unen cada extremo de la diagonal del cuadrado en marcha con sendos contiguos, el marcado sobre la semi-circunferencia y el reflejado respectivamente.
4 Construir el polígono que tiene como vértices:
- el punto sobre la semicircunferencia,
- uno de los extremos de la diagonal del cuadrado en marcha,
- el punto reflejado,
- el otro extremo de la diagonal
5 Desplazar el punto que se trazó sobre la semicircunferencia hasta que ocupe la posición en que parece un cuadrado.
Justificaciones y Controles
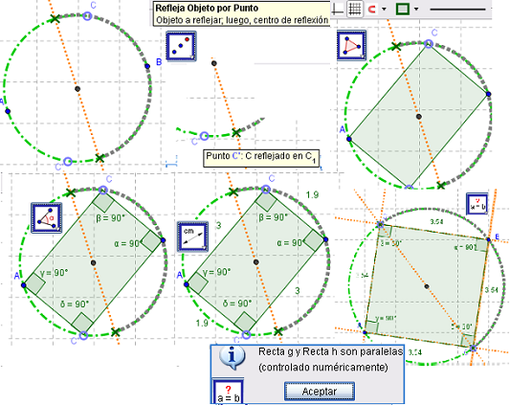
El boceto se traza de modo tal que el punto que se desplaza sobre la semicircunferencia, su reflejado y los contiguos - vértices de la diagonal - conformen...
- un rectángulo
- que deviene cuadrado cuando se lo lleva hasta uno de los de intersección - ambos son extremos del recorrido por el que hasta se lo podría animar.
Conviene controlar...
- de modo más certero este comportamiento, empleando las herramientas adecuadas para contar con información sobre valores y relaciones
- las argumentaciones respecto a las vinculaciones entre el resultado de los ensayos y lo que la construcción desencadena en todos los casos.
Un Quehacer a Proyectar y Compartir
Pese a que lo más evidente - desde la óptica docente - es que la primera de las actividades depende directamente del empleo de herramientas con las que es preciso familiarizarse, ambas se entrecruzan con operaciones sobre la construcción dinámica:
- en exploraciones - guiadas por un propósito - que van dando entidad a...
- justificaciones causales de los efectos de ciertas maniobras - ¿es rectángulo? - ¿siempre? - ¿cómo hacemos para asegurarlo? - ¿cuándo parece pasar a cuadrado? - ....
- las relaciones entre los elementos que es preciso develar para respaldar la cadena de causalidades
- las correlaciones entre efectos, trazado y propiedades en juego que requieren un estudio conceptual
- ... de hecho, es la necesidad de validar estas presunciones lo que da razón de ser a su estudio.
Este recorrido expone un modelo de quehacer matemático que, escasamente transitado en términos generales frente a los estudiantes y con ellos, permite proyectarlo como medio de formación que puede completarse en intercambios virtuales.
Herramientas para el Control de Ensayos y Presunciones
6 Emplear las herramientas necesarias para controlar qué tipo de cuadrilátero se ha construido. Por ejemplo:
- la que traza y mide sus
 ángulos para corroborar que, tal como parece, son rectos
ángulos para corroborar que, tal como parece, son rectos - la que
 mide la longitud de cada lado
mide la longitud de cada lado - la que informa sobre la
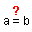 relación entre los segmentos de los lados y de las correspondientes rectas.
relación entre los segmentos de los lados y de las correspondientes rectas.
7 Procurar descripciones argumentadas sobre el tipo de cuadrilátero que se establece a medida que se desplaza el punto sobre la semicircunferencia.
Herramientas Propias para Completar las Disponibles
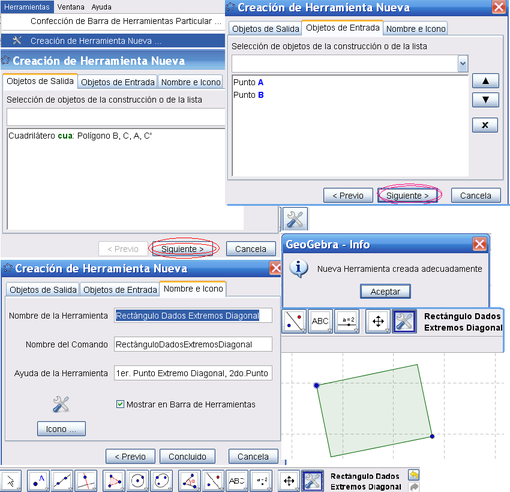
8 - Opción más Avanzada Dirigirse al manual para conocer la serie de pasos a partir de los cuáles, seleccionando el cuadrilátero creado como objeto de salida en la Nueva herramienta de la opción Creación de Herramienta Nueva del Menú de Herramientas, se puede crear la propia.
- En este caso, la que traza rectángulos (que pueden establecerse como cuadrados), dada su diagonal, como ilustra la siguiente figura.
- Habría que incluirlos en el listado correspondiente, si además del cuadrilátero (polígono), se deseara que otros elementos se expusieran en la salida (como los puntos vértices adicionales a los dados, los segmentos de lado, las rectas que los contienen, la semicircunferencia por la que se desplaza uno de los puntos de entrada, etc.).
- Una vez creada la herramienta, es posible cambiar el ícono que la acompaña así como otros detalles - nombre, ayuda -.