Puntos y Vectores

| Página en proceso de traducción. |
Los puntos y vectores pueden ingresarse en la Barra de Entrada, en Coordenadas cartesianas o polares (ver Números y Ángulos). Los puntos, también pueden crearse usando ![]() Punto y los vectores pueden crearse usando
Punto y los vectores pueden crearse usando ![]() Equipolente o
Equipolente o ![]() Vector o con una variedad de comandos.
Vector o con una variedad de comandos.
- Para ingresar un punto P o un vector v en Coordenadas cartesianas , se anota
P = (1, 0)ov = (0, 5) - Para ingresar un punto en la
 Hoja de Cálculo se nombra como su celda, por ejemplo
Hoja de Cálculo se nombra como su celda, por ejemplo A2 = (1, 0) - Para ingresar un punto en Coordenadas polares se escribe
P = (1; 0°)ov = (5; 90°)
Se puede acceder a las coordenadas de un punto, utilizando funciones predefinidas x() and y().
P=(1, 2) es un punto y v=(3, 4) un vector,x(P) da por resultado 1 y y(v) da por resultado 4.abs(Q) and arg(Q).Cálculos
En GeoGebra se puede hacer cálculos con puntos y vectores.
- Se puede crear el punto medio M de dos puntos A y B ingresando
M = (A + B) / 2en la Barra de Entrada. - La longitud de un vector v puede ser carculada usando
longitud = sqrt(v * v)orlongitud = Longitud(v)
- Puntos
Un punto puede quedar definido desde la Barra o Campo de Entrada por...
- sus tres coordenadas cartesianas
- CartesianasEjemplo:
C=(1,2,3)
- Cartesianas
- sus tres coordenadas esféricas
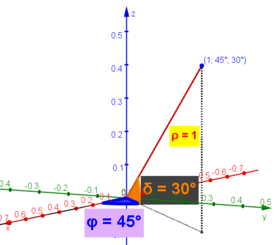
- EsféricasEjemplo: A=(1 ; 45°;30°)
- Esféricas
- (ρ, φ, δ) donde...
- ρ designa la distancia del punto al origen,
- φ designa la longitud (ángulo polar de la proyección del objeto sobre xOy, medido tras el eje x, entre 0° y 360°)
- δ la latitud, el ángulo tras el plano xOy (entre -90° y 90°)
A=(1;45°;30°)Ilustrando con Coordenadas
Vectores
- la longitud de un vector v con
longitud = sqrt(v * v)
Se puede operar con un punto, como A, para establecer otro. Así...
- Siendo A = (a, b), A + 1 crea otro punto, B, de coordenadas (a + 1, b + 1)
- Siendo A un número complejo a + b i, entonces...
- A + 1 crea otro, el número complejo a+1+bi y
- A + i, el número complejo a+ (b + 1) i
Producto Vectorial
Para dos puntos o dos vectores (a, b)⊗(c, d) da por resultado la coordenada-z del producto vectorial (a, b, 0)⊗(c, d, 0) como un simple número.
Similar sintaxis es válida para listas pero el resultado en tal caso, es una lista.
{1, 2} ⊗ {4, 5}da por resultado {0, 0, -3}{1, 2, 3} ⊗ {4, 5, 6}da {3, 6, -3} dado que el producto vectorial usual opera con listas.




