Pista:Expresiones Animadamente Parametrizadas

De GeoGebra Manual
- Pueden incluirse operadores diversos en la formulación de una función. Como en:
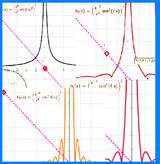
raízn(x^x(J) / x⁴ sen(y(J)x)^y(J), 4)en la que, siendo J unPunto[-x]que se puede desplazar o animar, el gráfico cambia según la posición de J.
Como la siguiente secuencia de expresiones según distintos valores de las enteras coordenadas de J en parsimoniosa animaciòn -. $\mathbf{\frac{1}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} \left( x \right)}{x}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{2}\left( 2 \; x \right)}{x^{2}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{3}\left( 3 \; x \right)}{x^{3}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\left|\operatorname{sen} \left( 4 \; x \right)\right|}{x^{2}}} $
Es interesante notar que en este caso, en lugar del valor de un Deslizador se emplean las coordenadas de un punto para notar las modificaciones que sufre la función.
La sección ¿Sabían que... ? incluye todas las pistas que salpican, como esta de Centro Babbage, la Página Principal.