Diferencia entre revisiones de «Pista:Determinando Complejos»

De GeoGebra Manual
| Línea 5: | Línea 5: | ||
:Estableciendo sendos puntos como '''''[[Números complejos|Número Complejo]]''''' en la pestaña '''Álgebra''' de su [[Cuadro de Propiedades|Caja de Propiedades]], informan las ''complejas soluciones''<br> | :Estableciendo sendos puntos como '''''[[Números complejos|Número Complejo]]''''' en la pestaña '''Álgebra''' de su [[Cuadro de Propiedades|Caja de Propiedades]], informan las ''complejas soluciones''<br> | ||
: | : | ||
| − | <small>La sección ''¿Sabían que... ? '' incluye [[ | + | <small>La sección ''¿Sabían que... ? '' incluye [[Pistas|''pistas'']] como esta de [http://www.centrobabbage.com ''Centro Babbage''], que ''salpican'' la [[Página Principal|Página Inicial]].</small> |
[[Category:Pistas]] | [[Category:Pistas]] | ||
Revisión del 14:06 18 sep 2014
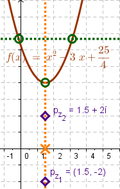
- Las raíces reales de una cuadrática f(x) se registran gráficamente por la ordenada de los puntos de intersección de f con el EjeX). Para las no reales, a partir de un punto A sobre f(x), se establece el vértice y luego el par:
- sc_1=PuntoMedio[Interseca[f, Mediatriz[A, Interseca[f, Recta[A, EjeX], 2]]], Interseca[EjeX, Mediatriz[A, Interseca[f, Recta[A, EjeX], 2]]]]
- sc_2=Refleja[PuntoMedio[Interseca|[f, Mediatriz[A, Interseca[f, Recta[A, EjeX], 2]]], Interseca[EjeX, Mediatriz[A, Interseca[f, Recta[A, EjeX], 2]]]], EjeX]
- Estableciendo sendos puntos como Número Complejo en la pestaña Álgebra de su Caja de Propiedades, informan las complejas soluciones
La sección ¿Sabían que... ? incluye pistas como esta de Centro Babbage, que salpican la Página Inicial.