Incluyendo Dibujos en la Vista Gráfica

Herramientas de Dibujo para Figuras Simétricas
- ¿Resulta productivo este escenario de exploración en que se parte de una construcción ya preparada - en que además de la flor aparecen otros dibujos en que se registra simetría - ?
- ¿Qué herramientas se emplean para crear la figura dinámica?
Preparativos
- Abrir una Nueva Ventana de GeoGebra.
- Ocultar la Vista Algebraica, la Barra de Entrada las coordenadas y ejes (en el Menú Vista).
Pasos de Construcción
| 1 | Nuevo punto A | |
| 2 | Mostrar el rótulo del punto A | |
| 3 | Recta de reflexión a través de dos puntos | |
| 4 | Reflexión de A en la recta para obtener el punto imagen A' | |
| 5 | Segmento entre el punto A y su imagenA' | |
| 6 | Activar el Rastro de los puntos A y A' | |
| 7 | Desplazar el punto A para ir trazando un dibujo dinámicamente |
Analizando
La posibilidad de dejar rastro deja una estela que tiene algunas características especiales:
- Es un fenómeno temporal. Cuando se actualizan los gráficos, desaparece.
- No puede guardarse y no queda expresado en la Vista Algebraica.
- Se borra con una combinación de teclas Ctrl + F. MacOS: Open Apple + F) o con la opción correspondiente del menú Vista – Actualiza Vista Gráfica (Limpia rastros).
Retocar la Construcción
| 8 | Insertar la imagen en la Vista Gráfica | |
| 9 | Ajustar la posición de la imagen intercalada. | |
| 10 | Fijarla como de fondo (pestaña Básico de la Caja de Diálogo de Propiedades). | |
| 11 | Reducir la opacidad de la image (pestaña Estilo de la Caja de Diálogo de Propiedades). |
Escalando y Transformando un Dibujo
Encuadre de Partida
Se dispondrá de una figura en la Vista Gráfica que se irá a:
- reflejar
- trasladar
- eventualmente, reducir o dilatar y/o
- distorsionar
El desafío será identificar:
- los ejes de reflexión,
- vectores de traslación y
- secuencia de transformaciones que lleven de la figura original a la última de sus versiones.
El contorno de un elemento de la imagen se hace coincidir aproximadamente con una cónica para tener un indicador que ayude a controlar si el recorrido que se indica es correcto.
Requerimientos y Preparativos
Requisitos
Es necesario:
- contar con el archivo, Ratón Miró Kandinsky, en cada equipo de trabajo.
- emplear la
 herramienta para insertar la correspondiente imagen en la hoja del boceto en marcha
herramienta para insertar la correspondiente imagen en la hoja del boceto en marcha - ubicar la imagen adecuadamente en la Vista Gráfica
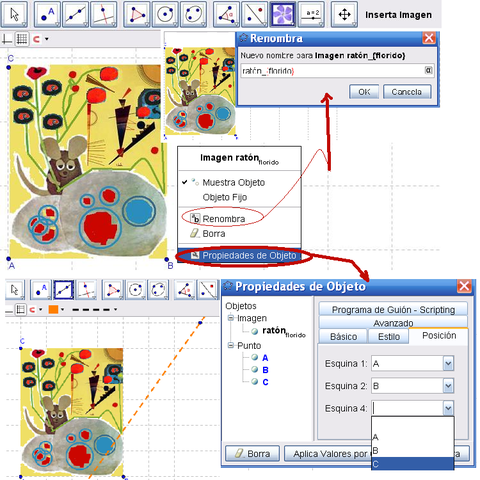
- crear los puntos A (en vértice el inferior izquierdo de la imagen), el B (en el inferior derecho) y el C (en el superior izquierdo) para que hagan las veces de esquinas del marco de la imagen, conformando originalmente un adecuado rectángulo como se ilustra en la primera sección de la figura.
- seleccionar la opción Renombra del Menú Contextual (que se despliega con un ¡¡clici¡¡ derecho sobre la imagen) para cambiarle el nombre de imagen1 a otro más ilustrativo, como se expone en la segunda sección de la figura
- desplegar nuevamente el Menú Contextual para indicar Propiedades del Objeto y pasar a la pestaña Posición del Cuadro de Propiedades como se ilustra en la tercera sección de la figura
- desplegar, pulsando la flecha derecha de la casilla de cada Esquina, las posiciones posibles para la número 1, eligiendo el punto A; B para la segunda y C para la tercera, como se ve a la derecha, en la última sección de la figura
- ubicar B y C más próximos a A de modo tal que la figura se reduzca sin distorsionarse
 y trazar una recta que hará las veces de eje de reflexión, como se ve a la izquierda, en la última sección de la figura
y trazar una recta que hará las veces de eje de reflexión, como se ve a la izquierda, en la última sección de la figura- añadir un par extra de
 rectas como para temer elementos alternativos y/o dstractores
rectas como para temer elementos alternativos y/o dstractores - distribuir un par de
 vectores para contar con la posibilidad de trasladar la imagen.
vectores para contar con la posibilidad de trasladar la imagen.
Desafío de Puesta en Marcha
- Condiciones
- Se pueden desplazar los puntos B y/o C para encuadrar adecuadamente la imagen de partida
- Puede elegirse...
- una de las rectas expuestas para que haga las veces de eje de reflexión de una transformación.
- uno de los vectores para proceder a trasladar el cuadro
- Requisito
- Hacer coincidir, con la mayor precisión posible, el resultante redondel del contorno de la piedra mayor en la imagen (tras distorsión , traslaciones y reflexiones de la obra original) con la silueta de una cónicas (trazada en violeta).
- Procurar la mejor concordancia en forma y posición entre la roca ovalada y la de la cónica.
- Decisiones
- ¿Cuál de las rectas podrían hacer las veces de eje de reflexión para lograrlo?
- ¿Cuál de los vectores dirigirían la traslación (o las traslaciones)?
- Control de Resultados
- ¿Cómo medir el grado de precisión de la coincidencia obtenida?
- Pistas Estratégicas
- Dicen que...
- es una estrategia adecuada, ir de atrás hacia adelante, remontando la cónica de llegada hacia la de partida para corroborar las transformaciones en sentido inverso
- los efectos de desplazar las rectas y/o los vectores permiten identificar qué rol cumplen en la secuencia de transformaciones o notar que son meros distractores
- Es conveniente compartir otras maniobras que podrían sumarse como recomendables a lo largo del quehacer.
- Dicen que...
Preparativos
- Verificar que se dispone del archivo de la obra en el o los equipos de trabajo.
- Seleccionar del Menú Apariencias la que convenga para la propuesta
- Cerrar la Vista Algebraica y activar la Barra de Estilo
- Desde la Barra de Estilo...
- esconder los ejes de coordenadas
- exponer la cuadrícula
- establecer la condición por la que se Ajusta a Cuadrícula cada elemento en la Vista Gráfica
- Emplear la
 herramienta para insertar la imagen, abriendo el archivo de la obra y proseguir con el instructivo que se detalla a continuación.
herramienta para insertar la imagen, abriendo el archivo de la obra y proseguir con el instructivo que se detalla a continuación.
Pasos de Construcción
| 1 | Insertar la imagen del archivo gráfico Ratón Miró Kandinsky en la zona izquierda de la Vista Gráfica | |
| 2 | Ubicar el punto A en el vértice inferior izquierdo de la obra, B en el derecho y C en la esquina superior izquierda. | |
| 3 | Establecer estos tres puntos como equinas apropiadas de la figura.
| |
| 4 | Trazar al menos dos rectas entre dos puntos indicados libremente en la Vista Gráfica | |
| 5 | Trazar al menos dos vectores entre dos puntos indicados libremente en la Vista Gráfica | |
| 6 | Seleccionar la imagen junto a los puntos A, B y C para...
| |
| 7 | Nota: Conviene cambiar la Opacidad del sombreado de la imagen en alguna de las versiones (original o reflejada) para distinguir una de otra.
| |
| 8 | Trasladar el reflejo por uno de los vectores. | |
| 9 | Marcar con un color y tamaño notorios, un punto cualquiera para reducir lo trasladado por un factor, como por ejemplo -1.5. | |
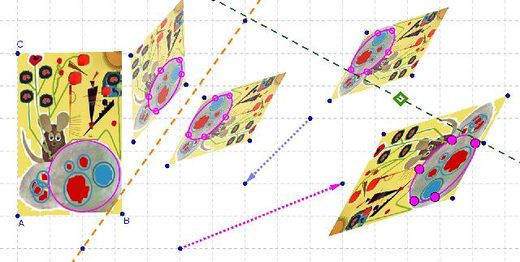
| 10 | En la primera versión de la imagen, la distorsionada, trazar con cinco puntos sobre el contorno de la piedra mayor, una cónica que se reproduzca por la secuencia de transformaciones recorrida, hasta la última, como se ve en la figura. |
El planteo queda completo con esta última maniobra.
Tal como queda es acaso demasiado obvio cuál es el recorrido de transformaciones, los ejes y los vectores y quizá solo se complique encontrar el punto y el factor de la dilatación final. Si se desea subir el nivel del reto, se podría ocultar el eje de reflexión en lugar de simplemente sumar otro como distractor.
Remontando las Transformaciones en Juego
Llegado a este punto, con el planteo listo, conviene intercambiar desafíos para que cada participante ponga en juego estrategias para...
- identificar qué vector y qué ejes se pusieron en juego y
- secuenciar las transformaciones de la imagen desde la primera versión a la última.
Controlando Ejes
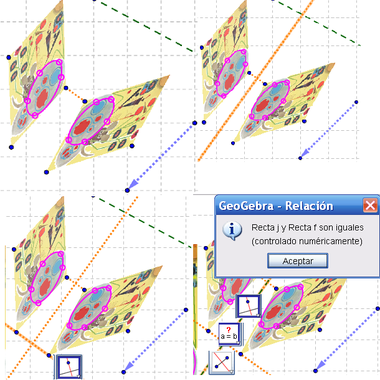
En la figura se muestra la secuencia de maniobras que lleva a...
1 Trazar la mediatriz entre sendos puntos, uniéndolos antes o después con un segmento.
2 Añadir la ![]() perpendicular a la mediatriz que pasa por uno de los puntos de otro vértice.
perpendicular a la mediatriz que pasa por uno de los puntos de otro vértice.
3 ![]() Compara ambas rectas para corroborar que coinciden.
Compara ambas rectas para corroborar que coinciden.
Instrumentando Propiedades de la Reflexión
De este modo, se controla la presunción respecto del eje y de la reflexión en sí empleando de modo instrumental una de las propiedades de la reflexión. La justificación de la validez de esta maniobra puede estudiarse conceptualmente entonces, cuando ya ha ganado razón de ser esta profundización al respecto.