Diferencia entre revisiones de «Función Raízn»

De GeoGebra Manual
| Línea 9: | Línea 9: | ||
::*'''<code>p_1(x) = k raízn(k x,k)</code>''', siendo ''k'' un valor determinado por un deslizador, traza el [[Vista Gráfica|gráfico]] acorde a la correspondiente expresión. Es interesante notar el modo en que gráfico y expresión resultante cambian a medida que se modifica (manualmente o por animación) el valor de ''k''. | ::*'''<code>p_1(x) = k raízn(k x,k)</code>''', siendo ''k'' un valor determinado por un deslizador, traza el [[Vista Gráfica|gráfico]] acorde a la correspondiente expresión. Es interesante notar el modo en que gráfico y expresión resultante cambian a medida que se modifica (manualmente o por animación) el valor de ''k''. | ||
::*'''<code>raízn(x^x(J) / x⁴ sen(y(J)x)^y(J), 4)</code>''' siendo '''J''' un punto, traza el [[Vista Gráfica|gráfico]] acorde a la correspondiente expresión resultante, según la posición de '''''J''''', como, por ejemplo:<br> | ::*'''<code>raízn(x^x(J) / x⁴ sen(y(J)x)^y(J), 4)</code>''' siendo '''J''' un punto, traza el [[Vista Gráfica|gráfico]] acorde a la correspondiente expresión resultante, según la posición de '''''J''''', como, por ejemplo:<br> | ||
| − | ::<center>$\sqrt[4]{\frac{x³ sen(-2x)² }{x⁴\;}\;}$</center><br>A continuaciòn se expone una secuencia de expresiones según distintos valores de las enteras coordenadas de ''J'' - siendo ''J'' un '''<code>[[Comando Punto|Punto[-x]]]</code>''' | + | ::<center>$\sqrt[4]{\frac{x³ sen(-2x)² }{x⁴\;}\;}$</center><br>A continuaciòn se expone una secuencia de expresiones según distintos valores de las enteras coordenadas de ''J'' - siendo ''J'' un '''<code>[[Comando Punto|Punto[-x]]]</code>''' en una parsimoniosa animaciòn -.}}<hr> |
:<center>$\mathbf{\frac{1}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} \left( x \right)}{x}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{2}\left( 2 \; x \right)}{x^{2}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{3}\left( 3 \; x \right)}{x^{3}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\left|\operatorname{sen} \left( 4 \; x \right)\right|}{x^{2}}} $</center><hr> | :<center>$\mathbf{\frac{1}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} \left( x \right)}{x}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{2}\left( 2 \; x \right)}{x^{2}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{3}\left( 3 \; x \right)}{x^{3}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\left|\operatorname{sen} \left( 4 \; x \right)\right|}{x^{2}}} $</center><hr> | ||
:{{Note|1=<br> | :{{Note|1=<br> | ||
| − | ::<hr>Es interesante notar que en este caso, en lugar de un [[Herramienta de Deslizador]] se emplean las [[Comando Coordenadas|coordenadas]] de un punto para notar las modificaciones que sufre la función.<br>Al respecto, si el punto ''J'' se ubicara sobre uno de los ejes, al darle [[Animación|animación]] se estarían observando los cambios del gráfico en función ya no exclusivamente de '''''x''''' ni sólo en el efecto sobre los valores de '''''y''''' sino de una variable adicional, dinámica .<hr> | + | ::<hr>Es interesante notar que en este último caso, en lugar del valor de un [[Herramienta de Deslizador|Deslizador]] se emplean las [[Comando Coordenadas|coordenadas]] de un punto para notar las modificaciones que sufre la función.<br>Al respecto, si el punto ''J'' se ubicara sobre uno de los ejes, al darle [[Animación|animación]] se estarían observando los cambios del gráfico en función ya no exclusivamente de '''''x''''' ni sólo en el efecto sobre los valores de '''''y''''' sino de una variable adicional, dinámica .<hr> |
}} | }} | ||
===[[Image:View-cas24.png]] En [[Vista Algebraica CAS|Vista CAS '''C'''<sub><small>omputación</small></sub>'''A'''<sub><small>lgebraica</small></sub>'''S'''<sub><small>imbólica</small></sub>]]=== | ===[[Image:View-cas24.png]] En [[Vista Algebraica CAS|Vista CAS '''C'''<sub><small>omputación</small></sub>'''A'''<sub><small>lgebraica</small></sub>'''S'''<sub><small>imbólica</small></sub>]]=== | ||
En esta [[Vista Algebraica CAS|vista]], se admiten formulaciones que contengan literales para operar simbólicamente y/o de aquellas con ''soluciones'' o raíces no reales. | En esta [[Vista Algebraica CAS|vista]], se admiten formulaciones que contengan literales para operar simbólicamente y/o de aquellas con ''soluciones'' o raíces no reales. | ||
:{{Note|1=<br>Ver también la sección de [[Operadores y Funciones Predefinidas]].}} | :{{Note|1=<br>Ver también la sección de [[Operadores y Funciones Predefinidas]].}} | ||
Revisión del 20:15 4 dic 2012
Funciones y Operaciones
- raízn( <Expresión> , N (número natural) )
- Calcula la raíz eNésima de la expresión dada.
- Ejemplos:
raízn(x^8, 2)da por resultado (|x|)⁴ y la representación correspondiente en la Vista Gráficaraízn(16, 4)da por resultado 2.
| Cuando en lugar de un càlculo, se ingresar una expresión que resulte dependiente de una variable, se crea una funciòn. El resultado, expresado en forma algebraica, es entonces, gráficado. Como se ilustra en uno de los ejemplos desarrollados más adelante. |
- Nota:
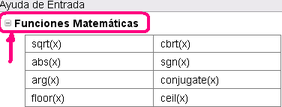
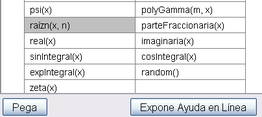
Para acceder directamente a cualquiera de las Funciones Predefinidas basta con:
Desplegarlas y expandir su listado pulsando el signo +
seleccionar la que corresponda y pulsar en el botón Pega. - Ejemplos:
p_1(x) = k raízn(k x,k), siendo k un valor determinado por un deslizador, traza el gráfico acorde a la correspondiente expresión. Es interesante notar el modo en que gráfico y expresión resultante cambian a medida que se modifica (manualmente o por animación) el valor de k.raízn(x^x(J) / x⁴ sen(y(J)x)^y(J), 4)siendo J un punto, traza el gráfico acorde a la correspondiente expresión resultante, según la posición de J, como, por ejemplo:
$\sqrt[4]{\frac{x³ sen(-2x)² }{x⁴\;}\;}$
A continuaciòn se expone una secuencia de expresiones según distintos valores de las enteras coordenadas de J - siendo J unPunto[-x]en una parsimoniosa animaciòn -.
$\mathbf{\frac{1}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} \left( x \right)}{x}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{2}\left( 2 \; x \right)}{x^{2}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\sqrt[4]{\frac{\operatorname{sen} ^{3}\left( 3 \; x \right)}{x^{3}}}}{\left|x\right|}} \; \; \; \; \; \; \mathbf{\frac{\left|\operatorname{sen} \left( 4 \; x \right)\right|}{x^{2}}} $ - Nota:
Es interesante notar que en este último caso, en lugar del valor de un Deslizador se emplean las coordenadas de un punto para notar las modificaciones que sufre la función.
Al respecto, si el punto J se ubicara sobre uno de los ejes, al darle animación se estarían observando los cambios del gráfico en función ya no exclusivamente de x ni sólo en el efecto sobre los valores de y sino de una variable adicional, dinámica .
 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
En esta vista, se admiten formulaciones que contengan literales para operar simbólicamente y/o de aquellas con soluciones o raíces no reales.
- Nota:
Ver también la sección de Operadores y Funciones Predefinidas.