Cuadrileteando

A lo largo de esta propuesta, clásica de Centro Babbage, conviene ir produciendo, paso a paso, la construcción del planteo en la Ventana de GeoGebra.
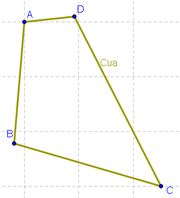
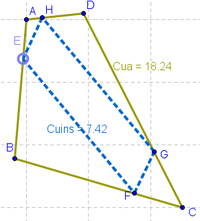
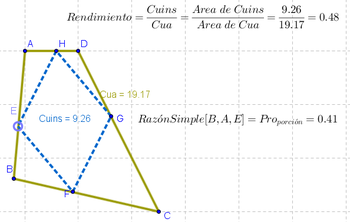
1 Empleando la Herramienta de Polígono, construimos un cuadrilátero cualquiera con vértices en los puntos A, B, C y D respectivamente (recordando volver a dar clic sobre el punto inicial A para "cerrar" el polígono). Para su mejor identificación, se activa el Menú Contextual, apelando a la alternativa desde la que se lo Renombra Cua.
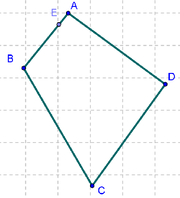
2 Con la Herramienta de Punto, creamos uno, E, sobre el segmento de lado que une los puntos A y B.
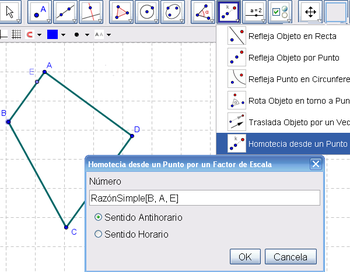
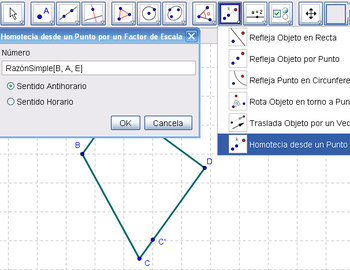
3 Empleando la Herramienta de Homotecia pasamos a crear otro punto en el lado opuesto al que une A y B, el tendido entre C y D, para obtener el resultado de la Homotecia[C, RazónSimple[B, A, E], D].
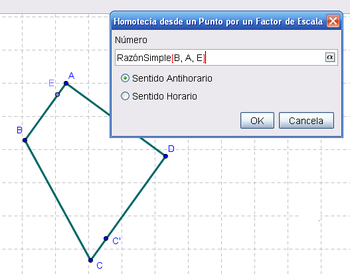
4 Otro tanto para crear la Homotecia[C, RazónSimple[B, A, E], B] sobre el lado que une A y D.
5 Del mismo modo para fijar la Homotecia[A, RazónSimple[B, A, E], D] en el lado que une D y A.
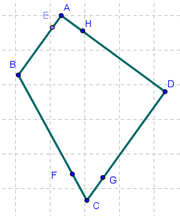
De este modo se completa el trazado de los cuatro puntos en cada lado...
6 Volvemos a apelar a la Herramienta de Polígono para crear el que une cada uno de los puntos recién creados sobre cada lado.
7 Es sencillo notar que todos los vértices del cuadrilátero A, B, C, D son libres y que al desplazarlos se modifica el tipo de cuadrilátero que acabamos de "inscribir" en Cua (el de ABCD).
8 Para mayor claridad a este cuadrilátero que une a los vértices EFGH, se lo Renombra Cuins y se destaca con diferente estilo a su único punto desplazable, el E. Apelando al Cuadro de Propiedades, se establece que de sendos cuadriláteros se expondrán tanto sus rótulos como sus valores de modo que se pueda apreciar rápidamente el modo en que se relacionan.
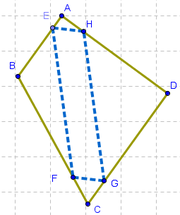
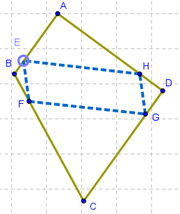
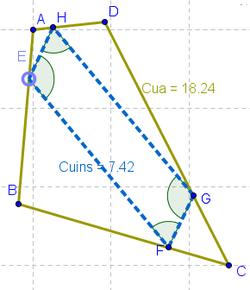
9 Podemos notar que al desplazar el punto E, los que de E dependen, ubicados sobre cada lado de ABCD, concuerdan con su movimiento para seguir ocupando la misma posición proporcional en los correspondientes lados de ABCD.. Si procuramos llevar E al punto medio entre A y B, otro tanto resultará con los vértices del "inscripto" en sus respectivos lados. Si se lo lleva hasta cerca de la novena parte de uno de los vértices del lado que ocupa, otro tanto sucederá con los demás vértices, F, G y H.
Cuadrilátero Cuins cuyos vértices son puntos que ocupan la misma posición proporcional en cada lado de Cua.
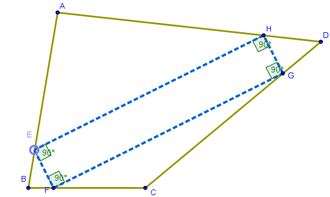
10 Para identificar con mayor facilidad las propiedades del cuadrilátero Cuins, se acude a la Herramienta de Ángulo que se le aplica en una maniobra simple.
11 Para explorar con un propósito guía que conduzca las observaciones, podemos plantearnos y/o plantearles a los estudiantes, una serie de desafíos. Por ejemplo...
- ¿Cómo harían para que el "inscripto" resulte un rombo o un cuadrado, lo primero que puedan lograr? o
- ¿Cómo creen que podría lograrse que llegara a configurar un trapecio o a un rectángulo?.
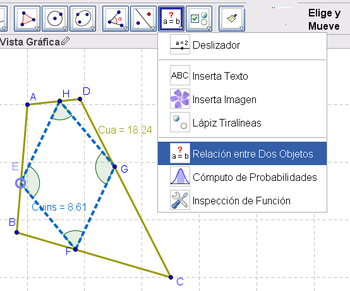
Algunas de las maniobras podría llevar a algún logro, al menos según se lo pudiera apreciar a simple vista y, en tal caso, sería importante cuestionarse sobre cómo controlar con mayor rigor, acudiendo a la Herramienta de Relación y/o a la información complementaria que ofrece la Vista Algebraica.
En cada ocasión, valdría analizar las condiciones que se procuraron para cada logro para poder reproducirlo sin necesidad de volver a tanteos que, en todo caso, se facilitan poniendo a la Vista la Cuadrícula y activando la alternativa Ajusta a Cuadrícula a partir de la Opción que establece la Atracción de Punto a Cuadrícula.
12 Los interrogantes que en el camino de las exploraciones pueden reiterarse apuntan a...
- ¿Cómo controlar que se llega a cada una de las metas propuestas? y
- ¿Qué herramientas conviene emplear y qué relaciones verificar?
- El método que se emplee para lograr cada uno de los cuadriláteros de distinto tipo, ¿será el único?
- ¿Será válido en todos los casos?
- ¿Cómo podríamos asegurarlo?
- ¿Habrá algunas metas imposibles de lograr?
- ¿Cómo podríamos convencernos de esta eventual imposibilidad?
13 Respecto, ya no de las posibles clasificaciones vinculadas a procedimientos acorde a propiedades de Cuins en relación a Cua, sino al régimen de cambio de las relaciones entre sus respectivas áreas, un planteo a indagar podría ser: ¿Cómo conseguir el máximo rendimiento de modo que al recortar el cuadrilátero inscripto Cuins se minimice el desperdicio de los "recortes" sobrantes de Cua?.
Incluso, ¿Cómo conseguir un rendimiento de un tercio del máximo posible?. Este tipo de interrogante incluye la necesidad de establecer, además, cuál es el máximo rendimiento.
Para llevar adelante esta indagación conviene establecer tanto la razón de las áreas como la de la proporción en que cada vértice de Cuins divide al correspondiente lado de Cua.
Además de recurrir a la Vista Algebraica para ir recabando esa información (una vez que se hizo el ingreso de los cálculos en la Barra de Entrada), es conveniente incluirla en la Vista Gráfica empleando la Herramienta de Texto.
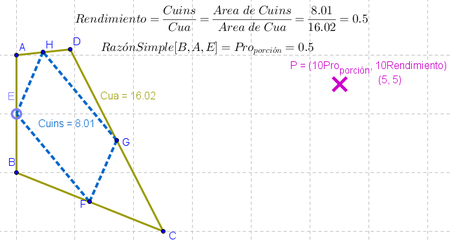
14 Para indagar de modo más completo el posible régimen de relaciones y de cambios entre la RazónSimple en juego y la razón entre sendas áreas, conviene establecer un punto de definición algebraica, ingresando en la Barra de Entrada, los valores variables de sus coordenadas como (10Pro_{porción}, 10Rendimiento) siendo Pro_{porción} la RazónSimple y Rendimiento la que se establece entre las áreas de Cuins a Cua.
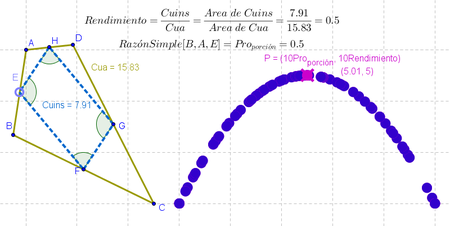
15 El modo preliminar de controlar cómo varía el Rendimiento en función de la Pro_{porción}, sería facilitar el registro en tanto se le Activa Rastro al punto de definición algebraica recién creado, tildando esta alternativa de su Menú Contextual, emergente cuando se lo selecciona y se pulsa el botón derecho del ratón o mouse.
Rastro que aparece a medida que se desplaza el punto E, vértice de Cuins, por el lado que ocupa en Cua.
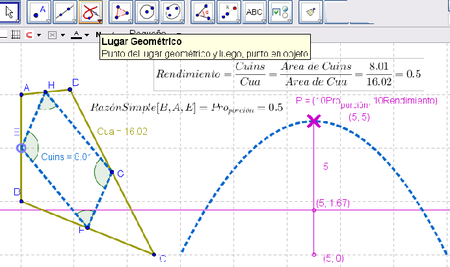
16 Es más perdurable y susceptible de mejor análisis que el rastro del punto de definición algebraica a medida que se desplaza E, el lugar geométrico correspondiente.
Los primeros cálculos pueden operarse sobre el lugar geométrico y, a medida que se progresa en su análisis, se pueda considerar con qué tipo de cónica pudiera tal trazo coincidir, apelando a la correspondiente herramienta y/o recabando los valores del punto en juego en la Hoja de Cálculo.
Esta multiplicidad de representaciones simultáneas permite un estudio de peculiar riqueza del régimen de relaciones y del de variaciones a partir de cada posible "punto de Vista".