Diferencia entre revisiones de «Comando Triangular»

Revisión del 23:38 4 oct 2014

Triangular[ <Límite Inferior>, <Límite Superior>, <Moda>, x ]: Establece y grafica, en el intervalo [mínimo, máximo] (siendo el mínimo el límite inferior y el máximo, el superior), con la moda indicada, la fdp, función de densidad de probabilidad (en inglés, pdf)^{probabilty density function} de la Triangular (triangular distribution o triangular en inglés).

Triangular[ <Límite Inferior>, <Límite Superior>, <Moda>, x, <Booleana_Acumulativa> ]: Si el valor booleano es falso^false, establece y grafica, tomando x como variable, la función de densidad de probabilidad de la distribución triangular y la acumulada correspondiente en caso contrario.

Triangular[ <Límite Inferior_mín>, <Límite Superior_máx>, <Moda>, <Valor de Variable> ]: Calcula, para el valor asignado a la variable, el de la fda^{función de distribución acumulativa} triangular en el intervalo correspondiente [mín, máx] con la moda indicada.
Así, Triangular[mín, máx, mod, v] calcula la probabilidad P(X ≤ v) siendo X la variable aleatoria a la que se asigna valor v; mín, máx y mod el de sendos parámetros.; Nota: Da por resultado la probabilidad para el valor dados de la abscisa (o el área bajo la curva de la distribución triangular a la izquierda de la coordenada v dada).; Ejemplo:
Triangular[3, 6, 4, 5] da como resultado en la Vista Algebraica 0.83

En Vista CAS C_omputaciónA_lgebraicaS_imbólica

En esta vista exclusivamente opera, del modo ya descripto, la siguiente alternativa:

Triangular[ <Límite Inferior_mín>, <Límite Superior_máx>, <Moda>, <Valor de Variable> ]: Ejemplos:
Triangular[ 0,5,2,2] da por resultado 0.4
Triangular[0,5,2,2] ñ + Triangular[1,3,2,2] q da por resultado \frac{5 q + 4 ñ}{10}

Nota: La alternativa exclusiva en esta vista, Solo admite literales para componer operaciones, como se ilustra en el ejemplo previo.

Ejemplos desde la Barra de Entrada gráficados y registrados en la Vista Algebraica

Ejemplos:

Triangular[ 0, 5, 2, 2] da por resultado 0.4

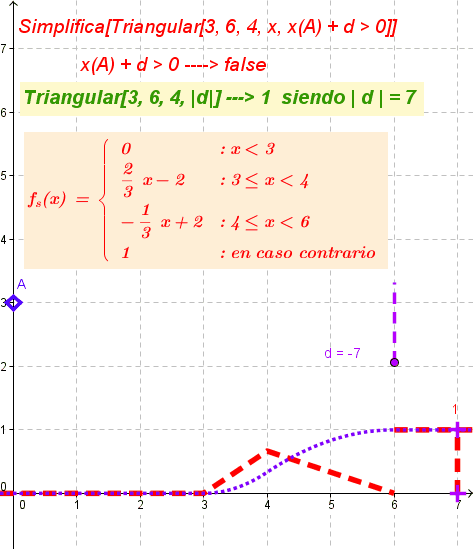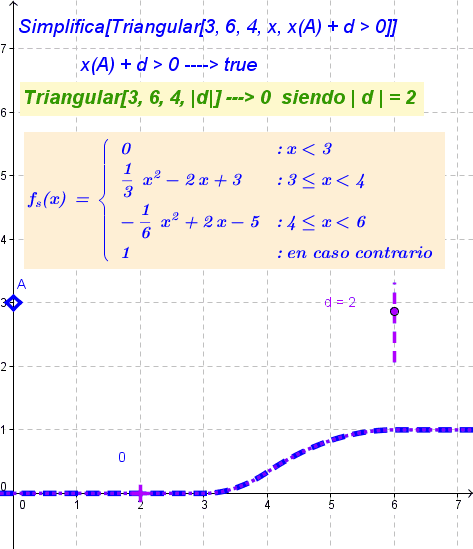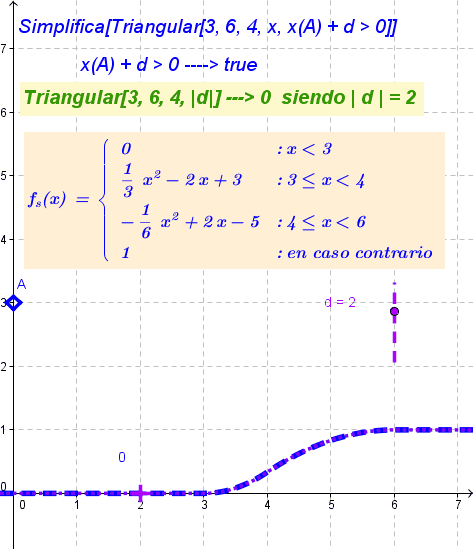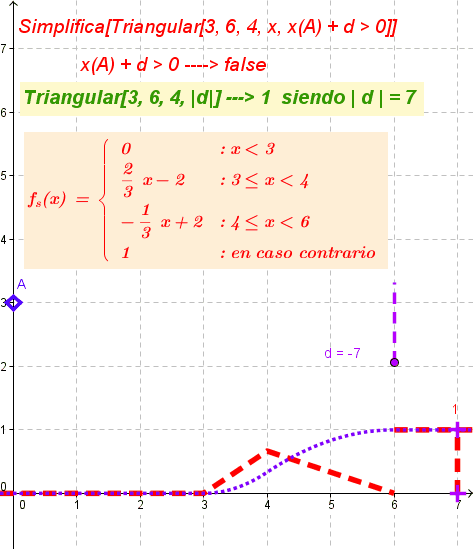
Desde la Barra de Entrada, Simplifica[ Triangular[3, 6, 4, x, x(A) + d > 0]] grafica la función resultante cuyo registro en la Vista Algebraica será equivalente a una de las siguientes expresiones según sea nula o negativa la abscisa de A más d o sea positiva, respectivamente.

Simplifica[Triangular[3, 6, 4, x, x(A) > 0]]

Valor de verdad falso - false - de la Booleana siendo x(A) ≤ 0

\left\{\begin{array}{ll} 0& : x < 3\\ \frac{2}{3} x - 2& : \left( x \geq 3 \right) \wedge \left( x < 4 \right)\\ -\frac{1}{3} x + 2& : \left( x \geq 3 \right) \wedge \left( x \geq 4 \right) \wedge \left( x < 6 \right)\\ 0& : \text{en caso contrario}\end{array}\right.Valor de verdad cierto - true - de la Booleana siendo x(A) > 0

\left\{\begin{array}{ll} 0& : x < 3\\ \frac{1}{3} x^{2} - 2 x + 3& : \left( x \geq 3 \right) \wedge \left( x < 4 \right)\\ -\frac{1}{6} x^{2} + 2 x - 5& : \left( x \geq 3 \right) \wedge \left( x \geq 4 \right) \wedge \left( x < 6 \right)\\ 1& : \text{en caso contrario}\end{array}\right.

@@ Línea 10: / Línea 10: @@
 En esta [[Vista CAS|vista]] exclusivamente opera, del modo ya descripto, la siguiente alternativa:
 ;Triangular[ <Límite Inferior<sub>mín</sub>>, <Límite Superior<sub>máx</sub>>, <Moda>, <Valor de Variable> ]
-:{{Examples|1= <br>'''<code>Triangular[ 0,5,2,2]</code>''' da por resultado ''0.4''<br>'''<code>Triangular[0,5,2,2] ñ + Triangular[1,3,2,2] q</code>''' da por resultado ''$\frac{5 \;  q  \; +  \; 4 \;  ñ}{10}$''}}
+:{{Examples|1= <br>'''<code>Triangular[ 0,5,2,2]</code>''' da por resultado ''0.4''<br>'''<code>Triangular[0,5,2,2] ñ + Triangular[1,3,2,2] q</code>''' da por resultado ''<math>\frac{5   q   +   4   ñ}{10}</math>''}}
 :{{Note|1=La alternativa exclusiva en esta [[Vista CAS|vista]], Solo admite literales para componer operaciones, como se ilustra en el ejemplo previo.}}
 <h5><center><small>Ejemplos desde la [[Barra de Entrada]] [[Vista Gráfica|gráficados]] y registrados en la [[Vista Algebraica]]</small></center></h5>
@@ Línea 17: / Línea 17: @@
 <br><center><code>Simplifica[Triangular[3, 6, 4, x, x(A) > 0]]</code></center><hr>
 <center>Valor de verdad falso - ''false'' -  de la ''Booleana'' siendo '''<code>x(A) ≤ 0</code>'''</center><br>&nbsp;&nbsp;
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \left\{\begin{array}{ll} 0& : x < 3\\ \frac{2}{3} \; x - 2& :  \left( x \geq 3 \right) \wedge  \left( x < 4 \right)\\ -\frac{1}{3} \; x + 2& : \left( x \geq 3 \right) \wedge  \left( x \geq 4 \right) \wedge  \left( x < 6 \right)\\ 0& : \text{en caso contrario}\end{array}\right.</math><br><hr><center>Valor de verdad cierto - ''true'' -  de la ''Booleana'' siendo '''<code>x(A) > 0</code>'''</center><br>&nbsp;&nbsp;
+&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \left\{\begin{array}{ll} 0& : x < 3\\ \frac{2}{3}  x - 2& :  \left( x \geq 3 \right) \wedge  \left( x < 4 \right)\\ -\frac{1}{3}  x + 2& : \left( x \geq 3 \right) \wedge  \left( x \geq 4 \right) \wedge  \left( x < 6 \right)\\ 0& : \text{en caso contrario}\end{array}\right.</math>Valor de verdad cierto - ''true'' -  de la ''Booleana'' siendo '''<code>x(A) > 0</code>'''&nbsp;&nbsp;
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \left\{\begin{array}{ll} 0& : x < 3\\ \frac{1}{3} \; x^{2} - 2 \; x + 3& :  \left( x \geq 3 \right) \wedge  \left( x < 4 \right)\\ -\frac{1}{6} \; x^{2} + 2 \; x - 5& :  \left( x \geq 3 \right) \wedge  \left( x \geq 4 \right) \wedge  \left( x < 6 \right)\\ 1& : \text{en caso contrario}\end{array}\right. </math><br><hr><!--
+&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \left\{\begin{array}{ll} 0& : x < 3\\ \frac{1}{3}  x^{2} - 2  x + 3& :  \left( x \geq 3 \right) \wedge  \left( x < 4 \right)\\ -\frac{1}{6}  x^{2} + 2  x - 5& :  \left( x \geq 3 \right) \wedge  \left( x \geq 4 \right) \wedge  \left( x < 6 \right)\\ 1& : \text{en caso contrario}\end{array}\right. </math><br><hr><!--
-<center>\left\{\begin{array}{}0 \;   \;  \;  \; \; x < 3\\\frac{x \; -\; 5}{3} \;   \;  \; \;  \; (x  ≥ \; 3) \; ∧ \; (x \; < \; 4) \; \\\frac{6 \;-  \; x}{6} \;   \;  \; \;  \; (x  ≥ \; 3) ∧ (x \; ≥ \; 4) ∧ (x \; < \; 6)\\0 \;   \;  \;  \; \; en  \; caso  \; contrario\end{array}  \right.  \)<small><small><sup>Abscisa de '''''A''''' no positiva</sup></small></small><br><br><math> \;  \; \; \;  \;  \; \left\lbrace \begin{array}{}0 \;   \;  \;  \; \;  \; \;  \;  \; \; \;  \; \; x < 3\\\frac{(x \;-  \; 3)^2}{3} \;   \;  \; \;  \; (x  ≥ \; 3) ∧ (x \; < \; 4)\\ 1 -\frac{(x \; - \; 6)^2}{6} \;   \;  \; \;  \; (x  ≥ \; 3) ∧ (x \; ≥ \; 4) ∧ (x \; < \; 6) \\1 \;   \;  \;  \; \; en  \; caso  \; contrario\end{array}  \right.  </math><small><small><sub>Abscisa de '''''A''''' positiva</sub></small></small></center>-->
+<center>\left\{\begin{array}{}0          x < 3\\\frac{x  - 5}{3}          (x  ≥  3)  ∧  (x  <  4)  \\\frac{6 -   x}{6}          (x  ≥  3) ∧ (x  ≥  4) ∧ (x  <  6)\\0          en   caso   contrario\end{array}  \right.  \)<small><small><sup>Abscisa de '''''A''''' no positiva</sup></small></small><br><br><math>          \left\lbrace \begin{array}{}0                      x < 3\\\frac{(x -   3)^2}{3}          (x  ≥  3) ∧ (x  <  4)\\ 1 -\frac{(x  -  6)^2}{6}          (x  ≥  3) ∧ (x  ≥  4) ∧ (x  <  6) \\1          en   caso   contrario\end{array}  \right.  </math><small><small><sub>Abscisa de '''''A''''' positiva</sub></small></small></center>-->
 <!--
 ;Triangular[ <Límite Inferior>, <Límite Superior>, <Moda>, <Valor de Variable> ]
 :Calcula, para el valor asignado a la variable, el de la función de la [[:w:es:Distribución Triangular|distribución triangular]] acumulativa.<br>Así, '''Triangular[mín, máx, mod, v]''' calcula la probabilidad ''P(X ≤ v)'' siendo ''X'' la [[:w:es:Variable_aleatoria|variable aleatoria]]; ''v'', el valor asignado y ''mín'', ''máx'' y ''mod'',  los de los tres primeros parámetros.
 -->

Diferencia entre revisiones de «Comando Triangular»

Revisión del 23:38 4 oct 2014

Triangular

Categorías de Comandos (todos)

En Vista CAS ComputaciónAlgebraicaSimbólica

Ejemplos desde la Barra de Entrada gráficados y registrados en la Vista Algebraica

En Vista CAS C_omputaciónA_lgebraicaS_imbólica