Diferencia entre revisiones de «Comando Longitud»

De GeoGebra Manual
| Línea 8: | Línea 8: | ||
:{{Note| Si los puntos dados no pertenecieran al gráfico de la función o de la curva, sus abscisas determinarán el intervalo correspondiente.}} | :{{Note| Si los puntos dados no pertenecieran al gráfico de la función o de la curva, sus abscisas determinarán el intervalo correspondiente.}} | ||
---- | ---- | ||
| − | ;Longitud[ <Lista o Texto> ]: Da por resultado el número de elementos que contiene la lista o el de caracteres del texto. | + | ;Longitud[ <Lista o Texto> ]:Da por resultado el número de elementos que contiene la lista o el de caracteres del texto. |
---- | ---- | ||
;Longitud[ <Curva>, <Número t1>, <Número t2> ]:Da por resultado la longitud de la curva entre los valores paramétricos ''t1'' y ''t2''. | ;Longitud[ <Curva>, <Número t1>, <Número t2> ]:Da por resultado la longitud de la curva entre los valores paramétricos ''t1'' y ''t2''. | ||
Revisión del 16:55 28 abr 2013
Longitud
Categorías de Comandos (todos)
- Longitud[ <Vector o Punto (con tal vector de posición)> ]
- Da por resultado la longitud del módulo del vector dado o del determinado por la posición del punto indicado. Así, Longitud[A], establece la longitud del módulo del vector posición de A.
- Longitud[ <Segmento> ]
- Establece la longitud del segmento.
- Ejemplo:
Longitud[ Segmento[(2, 1), (0, -2)] ]da por resultado 3.61. - Longitud[ <[Función>, <Valor x Inicial>, <Valor x Final> ]
- Da por resultado la longitud del tramo de la función en el intervalo. Así Longitud[f, x1, x2] establece la de f entre [x1, x2] y Longitud[f, 0, 1], la de f entre x= 0 y x = 1.
- Ejemplo:
Longitud[2 x, 0, 1]da por resultado 2.23606797749979, aproximación a \sqrt{5}.
- Longitud[ <Función o Curva>, <Punto Inicial>, <Punto Final> ]
- Da por resultado la longitud, entre sendos puntos, del gráfico de la función o la del tramo de la curva .
- Nota: Si los puntos dados no pertenecieran al gráfico de la función o de la curva, sus abscisas determinarán el intervalo correspondiente.
- Longitud[ <Lista o Texto> ]
- Da por resultado el número de elementos que contiene la lista o el de caracteres del texto.
- Longitud[ <Curva>, <Número t1>, <Número t2> ]
- Da por resultado la longitud de la curva entre los valores paramétricos t1 y t2.
- Longitud[ <Lugar Geométrico> ]
- Siendo el comando Perímetro el que establece la longitud del lugar geométrico, Longitud informa sobre la cantidad de puntos que lo componen.
 Atención: Para más detalles, ver el ejemplo en el artículo sobre el comando Primero.
Atención: Para más detalles, ver el ejemplo en el artículo sobre el comando Primero.
- Nota: Ver también la herramienta
 Distancia o Longitud.
Distancia o Longitud.
- Longitud[ <Arco> ]
- Da por resultado la longitud del arco del contorneado curvo de la sección circular correspondiente.
- Longitud[ <Sector> ]
- Da por resultado la longitud del arco que contornea al sector.
- Nota: La herramienta de
 Distancia o Longitud muestra el perímetro del sector.
Distancia o Longitud muestra el perímetro del sector.
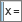 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
- Longitud[ <Función>, <Número t1>, <Número t2> ]
- Calcula la longitud del gráfico de una función desde el punto x=t1 al punto x=t2.
- Longitud[ <Función>, <Variable a>, <Número t1>, <Número t2> ]
- Calcula la longitud del gráfico de una función desde el punto a=t1 al punto a=t2.
- Ejemplo:
Longitud[2 a, a, 0, 1]da por resultado \sqrt{5}. - Longitud[ <Curva>, <Número t1>, <Número t2> ]
- Calcula la longitud de la curva desde el punto x=t1 a x =t2.
- Longitud[ <Curva>, <Variable a>, <Número t1>, <Número t2> ]
- Calcula la longitud de la curva desde el punto a=t1 hasta a =t2.
- Longitud[ <Segmento> ]
- Establece la longitud del segmento.
- Ejemplo:
Longitud[ Segmento[(2, 1), (0, -2)] ]da por resultado 3.61.
- Nota: Ver también la herramienta de
 Distancia o Longitud; el comando Perímetro y el ejemplo que se ofrece a continuación.
Distancia o Longitud; el comando Perímetro y el ejemplo que se ofrece a continuación.
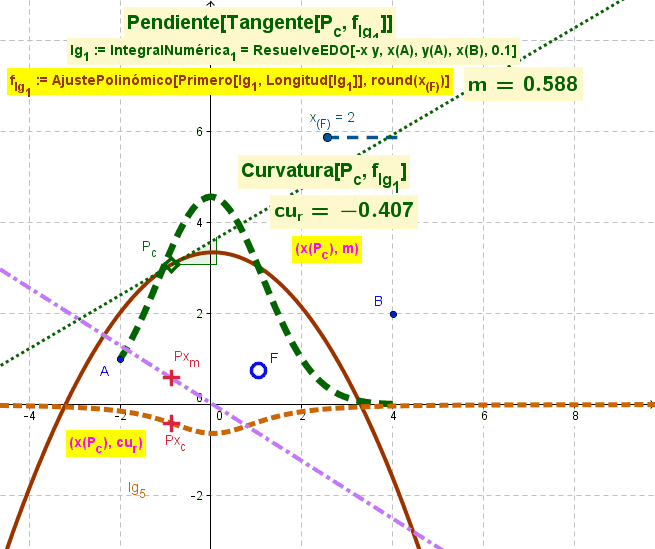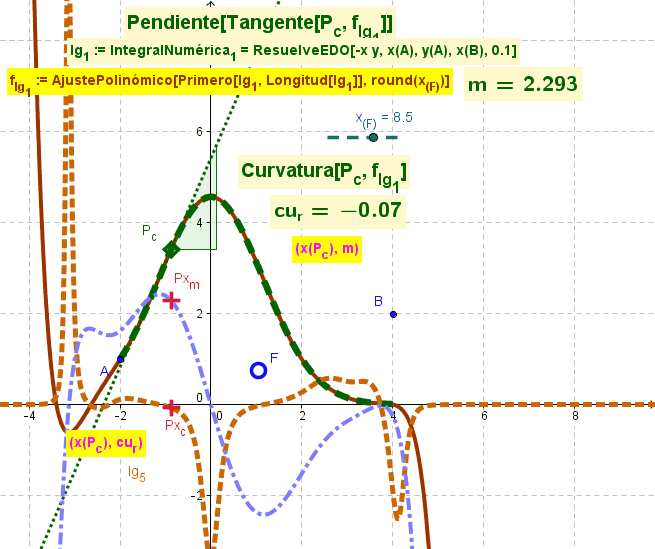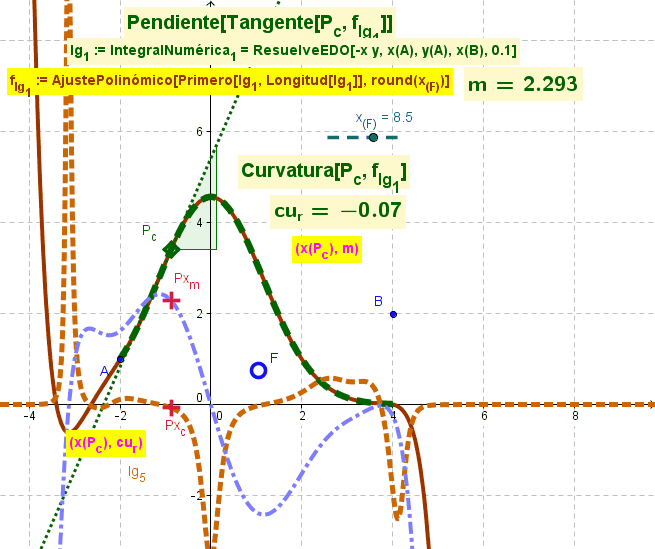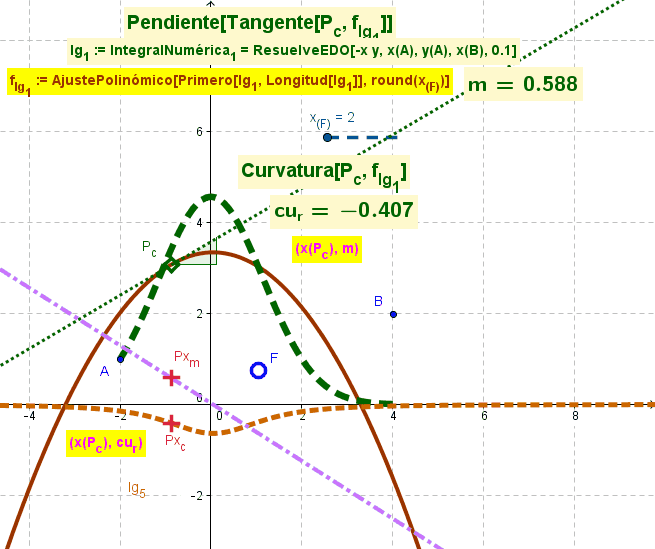
Primeros Puntos en Ajuste
Se parte de una función surgida de un AjustePolinómico acotado por el valor del deslizador en marcha para tomar sólo los Primeros x_F puntos en ese AjustePolinómico.
AjustePolinómico desde los puntos de un lugar geométrico representativo del ResuelveEDO (resolución de la ecuación diferencial ordinaria);f_{lg_1} := AjustePolinómico[Primero[lg_1, Longitud[lg_1]], round(x_{(F)})]