Diferencia entre revisiones de «Comando Límite»

De GeoGebra Manual
| Línea 8: | Línea 8: | ||
;Límite[ <Expresión>, <Valor> ]:Da por resultado el límite de la expresión para el valor indicado, de su variable principal. {{OJo|1=La expresión puede ser una función multvariable y/o incluir literales.}} | ;Límite[ <Expresión>, <Valor> ]:Da por resultado el límite de la expresión para el valor indicado, de su variable principal. {{OJo|1=La expresión puede ser una función multvariable y/o incluir literales.}} | ||
:{{Note|1='''<code><nowiki>Límite[f(w), m]</nowiki></code>''' establece el límite de ''f'' para ''w tendiendo a m'' como ilustran los siguientes ejemplos.}} | :{{Note|1='''<code><nowiki>Límite[f(w), m]</nowiki></code>''' establece el límite de ''f'' para ''w tendiendo a m'' como ilustran los siguientes ejemplos.}} | ||
| − | :{{Examples|1=<br><br>'''<code>Límite[((ñ ü (1-cos(x)))/x^2)+ñ, 0 ]</code>''' da | + | :{{Examples|1=<br><br>'''<code>Límite[((ñ ü (1-cos(x)))/x^2)+ñ, 0 ]</code>''' da <math>\frac{(ñ ü + 2 ñ) }{2}</math> el límite de:<br><math>\frac{(ñ ü (1 - cos(x)))}{x² }+ ñ </math> mientras...<br>'''<code>Límite[((ñ ü (1-cos(x))) / x^2)+ñ, ñ, 0 ]</code>''' da ''0''<br><br>'''<code><nowiki>Límite[a sin(x)/x, 0]</nowiki></code>''' da ''a''<br><br>'''<code><nowiki>Límite[ñ sen(t)/t, 0]</nowiki></code>''' da ''ñ''<br>'''<code><nowiki>Límite[ cos(x)/x, 0]</nowiki></code>''' da por resultado el signo '''''?''''' con el que en esta [[Vista CAS|vista]] se indica que no está definido el límite en cuestión.}}<hr> |
:{{OJo|1=<br>No todos los límites pueden calcularse y en tales casos aparecerá '''indefinido''' o, en la [[Vista CAS|Vista CAS]], el signo '''''?''''' por respuesta, del mismo modo que en las ocasiones en que el resultado ''correcto'' resulte precisamente ese.<br>Para obtener los límites de una función definida por tramos, están disponibles los comandos [[Comando LímiteSuperior|LímiteSuperior]] y/o [[Comando LímiteInferior|LímiteInferior]].<br> | :{{OJo|1=<br>No todos los límites pueden calcularse y en tales casos aparecerá '''indefinido''' o, en la [[Vista CAS|Vista CAS]], el signo '''''?''''' por respuesta, del mismo modo que en las ocasiones en que el resultado ''correcto'' resulte precisamente ese.<br>Para obtener los límites de una función definida por tramos, están disponibles los comandos [[Comando LímiteSuperior|LímiteSuperior]] y/o [[Comando LímiteInferior|LímiteInferior]].<br> | ||
}} | }} | ||
:{{Example|1=<br>Dada la [[Funciones|función]] '''''Si[x < 1, x², -2x]''''', lo adecuado es calcular sendos límites, a izquierda y derecha con... | :{{Example|1=<br>Dada la [[Funciones|función]] '''''Si[x < 1, x², -2x]''''', lo adecuado es calcular sendos límites, a izquierda y derecha con... | ||
:*'''<code><nowiki>LímiteInferior[Si[x < 1, x², -2x], 1]</nowiki></code>''' da por resultado ''1'' y | :*'''<code><nowiki>LímiteInferior[Si[x < 1, x², -2x], 1]</nowiki></code>''' da por resultado ''1'' y | ||
| − | :*'''<code><nowiki>LímiteSuperior[Si[x < 1, x², -2x], 1]</nowiki></code>''' da ''-2'' | + | :*'''<code><nowiki>LímiteSuperior[Si[x < 1, x², -2x], 1]</nowiki></code>''' da ''-2'' |
}}<hr> | }}<hr> | ||
:{{Note|1=Ver también los comandos [[Comando Asíntota|Asíntota]], [[Comando LímiteSuperior|LímiteSuperior]] y [[Comando LímiteInferior|LímiteInferior]].}} | :{{Note|1=Ver también los comandos [[Comando Asíntota|Asíntota]], [[Comando LímiteSuperior|LímiteSuperior]] y [[Comando LímiteInferior|LímiteInferior]].}} | ||
Revisión del 00:46 5 oct 2014
Límite
Categorías de Comandos (todos)
- Limite[ <Función>, <Valor numérico> ]
- Calcula el limite (límit en inglés) de la función para el valor fijado de su variable principal.
 Atención: Puede incluso ser infinitocon un signo u otro el valor al que tiende y/o el resultado.
Atención: Puede incluso ser infinitocon un signo u otro el valor al que tiende y/o el resultado.
- Ejemplos:
Límite[cos(x)/x,0]resulta indefinido ya que no está definido tal límite para x tendiendo a 0Límite[(x^2+x)/ x^2, +∞]da por resultado 1
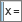 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
En esta vista se admiten literales en operaciones simbólicas y, a la descripta, se suma la siguiente sintaxis exclusiva;
- Límite[ <Expresión>, <Variable>, <Valor> ]
- Calcula el límite de la expresión multivariable dada para el valor fijado de la variable indicada. Así, Límite[f, v, t] establece el límite de f para el valor t de la variable v.
- Ejemplo:
Límite[ñ sen(w)/w, ñ, 0]da 0 yLímite[ñ sen(w)/w, w, 0]da ñ - Límite[ <Expresión>, <Valor> ]
- Da por resultado el límite de la expresión para el valor indicado, de su variable principal.
 Atención: La expresión puede ser una función multvariable y/o incluir literales.
Atención: La expresión puede ser una función multvariable y/o incluir literales.
- Nota:
Límite[f(w), m]establece el límite de f para w tendiendo a m como ilustran los siguientes ejemplos. - Ejemplos:
Límite[((ñ ü (1-cos(x)))/x^2)+ñ, 0 ]da \frac{(ñ ü + 2 ñ) }{2} el límite de:
\frac{(ñ ü (1 - cos(x)))}{x² }+ ñ mientras...Límite[((ñ ü (1-cos(x))) / x^2)+ñ, ñ, 0 ]da 0Límite[a sin(x)/x, 0]da aLímite[ñ sen(t)/t, 0]da ñLímite[ cos(x)/x, 0]da por resultado el signo ? con el que en esta vista se indica que no está definido el límite en cuestión.
 Atención:
Atención:
No todos los límites pueden calcularse y en tales casos aparecerá indefinido o, en la Vista CAS, el signo ? por respuesta, del mismo modo que en las ocasiones en que el resultado correcto resulte precisamente ese.
Para obtener los límites de una función definida por tramos, están disponibles los comandos LímiteSuperior y/o LímiteInferior.
- Ejemplo:
Dada la función Si[x < 1, x², -2x], lo adecuado es calcular sendos límites, a izquierda y derecha con...LímiteInferior[Si[x < 1, x², -2x], 1]da por resultado 1 yLímiteSuperior[Si[x < 1, x², -2x], 1]da -2
- Nota: Ver también los comandos Asíntota, LímiteSuperior y LímiteInferior.




