Diferencia entre revisiones de «Comando IntegralN»

De GeoGebra Manual
| Línea 11: | Línea 11: | ||
===[[Image:View-cas24.png]] [[Comandos Específicos CAS (Cálculo Avanzado)|En]] la [[Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== | ===[[Image:View-cas24.png]] [[Comandos Específicos CAS (Cálculo Avanzado)|En]] la [[Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== | ||
Se admiten literales en operaciones simbólicas y, además de la previa, la alternatica de indicar la variable de integración. Lo que, a su vez, inhabilita la graficación:<small><center>{{Attention|1=Exclusiva de [[Vista CAS|Vista CAS]]}}</center></small> | Se admiten literales en operaciones simbólicas y, además de la previa, la alternatica de indicar la variable de integración. Lo que, a su vez, inhabilita la graficación:<small><center>{{Attention|1=Exclusiva de [[Vista CAS|Vista CAS]]}}</center></small> | ||
| − | ;IntegralN[ <Función>, <Variable<sub>t</sub>>, <Valor Inicial<sub>t<sub>a</sub></sub>>, <Valor Final<sub>t<sub>b</sub></sub>> ]:Establece numéricamente, el valor de la integral de la [[Funciones|función]] ''f'' definida entre el valor inicial y el final, respecto de la variable ''t'' indicada: | + | ;IntegralN[ <Función>, <Variable<sub>t</sub>>, <Valor Inicial<sub>t<sub>a</sub></sub>>, <Valor Final<sub>t<sub>b</sub></sub>> ]:Establece numéricamente, el valor de la integral de la [[Funciones|función]] ''f'' definida entre el valor inicial y el final, respecto de la variable ''t'' indicada: <math>\int_a^bf(t)\mathrm{d}t</math>. |
:{{Example|1=Con decimales según [[Menú de Opciones#Redondeo|''Redondeo'']]...<br><br>'''<code><nowiki>IntegralN[ℯ^(-a^2), a, 0, 1]</nowiki></code>''' da ''0.7468''.<br><br>'''<code><nowiki>IntegralN[ℯ^(-j^2), j, 0, 1]</nowiki></code>''' da ''0.75''<br><br>'''<code>IntegralN[1/x,1,2]</code>''' da ''0.69'' dando '''<code>Integral[1/x,1,2]</code>''' igual [[Herramienta de Valor Numérico|valor]]<small>[[Archivo:Mode numeric.png|26px]]</small> ''0.69'' mientras '''<code>Integral[1/x,1,2]</code>''', en cambio, se [[Herramienta de Evalúa|evalúa]] como [[Archivo:Mode evaluate.png]] ''ln(2)''<br><br>'''<code><nowiki>IntegralN[ℯ^(-x), 0, 1]</nowiki></code>''' da ''0.632'' a comparar con '''<code><nowiki>Integral[ℯ^(-x), 0, 1]</nowiki></code>''' que da <math> \frac{e-1}{e}</math>.}} | :{{Example|1=Con decimales según [[Menú de Opciones#Redondeo|''Redondeo'']]...<br><br>'''<code><nowiki>IntegralN[ℯ^(-a^2), a, 0, 1]</nowiki></code>''' da ''0.7468''.<br><br>'''<code><nowiki>IntegralN[ℯ^(-j^2), j, 0, 1]</nowiki></code>''' da ''0.75''<br><br>'''<code>IntegralN[1/x,1,2]</code>''' da ''0.69'' dando '''<code>Integral[1/x,1,2]</code>''' igual [[Herramienta de Valor Numérico|valor]]<small>[[Archivo:Mode numeric.png|26px]]</small> ''0.69'' mientras '''<code>Integral[1/x,1,2]</code>''', en cambio, se [[Herramienta de Evalúa|evalúa]] como [[Archivo:Mode evaluate.png]] ''ln(2)''<br><br>'''<code><nowiki>IntegralN[ℯ^(-x), 0, 1]</nowiki></code>''' da ''0.632'' a comparar con '''<code><nowiki>Integral[ℯ^(-x), 0, 1]</nowiki></code>''' que da <math> \frac{e-1}{e}</math>.}} | ||
:{{Note|1=Ver también los siguientes comandos: | :{{Note|1=Ver también los siguientes comandos: | ||
Revisión del 06:20 19 nov 2014
IntegralN
Categorías de Comandos (todos)
- IntegralN[ <Función>, <Valor x Iniciala>, <Valor x Finalb> ]
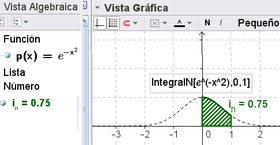
- Establece numéricamente y grafica, la integral de la función f definida entre el valor inicial y el final:
\int_a^bf(x)\mathrm{d}x - Ejemplos:
IntegralN[ℯ^(-x^2), 0, 1]da 0.75 e ilustra la representación gráfica correspondiente a ese tramo de integral definida de la función.IntegralN[1/x,1,2]da 0.693147180559945 (Opción : 15 decimales)IntegralNl[ℯ^(-x), 0, 1]da 0.632IntegralNl[ℯ^(-x), 0, 1]da 0.632120558828558 (Opción : 15 decimales)IntegralN[ℯ^(-x^2), 0, 2]da 0.88 e ilustra ese tramo de función coloreando, además, el área inferior en la Vista Gráfica
- Nota: El resultado de lo ingresado en la Barra de Entrada también se grafica.
 Atención: Si bien desde la Barra de Entrada puede llegar a ser posible ingresar el comando con los siguientes argumentos: IntegralN[ <Función>, <x ó y ó z>, <Valor-x-Iniciala>, <x-Finalb> ] es importante notar que lo que se establece numéricamente, no será la integral de la función f definida entre el valor inicial y el final, respecto de la variable x, y o z.
Atención: Si bien desde la Barra de Entrada puede llegar a ser posible ingresar el comando con los siguientes argumentos: IntegralN[ <Función>, <x ó y ó z>, <Valor-x-Iniciala>, <x-Finalb> ] es importante notar que lo que se establece numéricamente, no será la integral de la función f definida entre el valor inicial y el final, respecto de la variable x, y o z.
Será, en cambio, la IntegralEntre la primera función indicada y la siguiente entrada como .función. no como variable.
 En la Vista ComputaciónAlgebraicaSimbólica
En la Vista ComputaciónAlgebraicaSimbólica
Se admiten literales en operaciones simbólicas y, además de la previa, la alternatica de indicar la variable de integración. Lo que, a su vez, inhabilita la graficación:
| Exclusiva de Vista CAS |
- IntegralN[ <Función>, <Variablet>, <Valor Inicialta>, <Valor Finaltb> ]
- Establece numéricamente, el valor de la integral de la función f definida entre el valor inicial y el final, respecto de la variable t indicada: \int_a^bf(t)\mathrm{d}t.
- Ejemplo: Con decimales según Redondeo...
IntegralN[ℯ^(-a^2), a, 0, 1]da 0.7468.IntegralN[ℯ^(-j^2), j, 0, 1]da 0.75IntegralN[1/x,1,2]da 0.69 dandoIntegral[1/x,1,2]igual valor 0.69 mientras
0.69 mientras Integral[1/x,1,2], en cambio, se evalúa como ln(2)
ln(2)IntegralN[ℯ^(-x), 0, 1]da 0.632 a comparar conIntegral[ℯ^(-x), 0, 1]que da \frac{e-1}{e}. - Nota: Ver también los siguientes comandos: