Diferencia entre revisiones de «Comando Integral»

De GeoGebra Manual
m (Texto reemplazado: «;([a-zA-Z0-9]*)\[(.*)\]» por «;$1($2)») |
|||
| Línea 1: | Línea 1: | ||
<noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|cas=true|function|Integral}} | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|cas=true|function|Integral}} | ||
===→ Integral Indefinida / Primitiva=== | ===→ Integral Indefinida / Primitiva=== | ||
| − | ;Integral | + | ;Integral( <Función> ):Establece y [[Vista Gráfica|grafica]] la primitiva de la función respecto de la variable principal. |
:{{Example|1=<br>'''<code><nowiki>Integral[x^3]</nowiki></code>''' da por resultado ''0.25 x⁴'' y [[Vista Gráfica|grafica]] esta primitiva.}}}<!-- | :{{Example|1=<br>'''<code><nowiki>Integral[x^3]</nowiki></code>''' da por resultado ''0.25 x⁴'' y [[Vista Gráfica|grafica]] esta primitiva.}}}<!-- | ||
{{beta_manual|version=4.2|1=<small>Variante Adicional<hr></small> | {{beta_manual|version=4.2|1=<small>Variante Adicional<hr></small> | ||
}} --> | }} --> | ||
| − | ;Integral | + | ;Integral( <Función>, <Variable> ):Establece la integral indefinida parcial de la función respecto de la variable indicada. |
:{{OJo|1=Desde la [[Barra de Entrada]] solo se puede indicar como variable '''<code>x</code>''' o '''<code>y</code>''' o '''<code>z</code>''' de una eventual función multivariable dada.}} | :{{OJo|1=Desde la [[Barra de Entrada]] solo se puede indicar como variable '''<code>x</code>''' o '''<code>y</code>''' o '''<code>z</code>''' de una eventual función multivariable dada.}} | ||
:{{Examples|1=<br>'''<code><nowiki>Integral[x³ + 3 x y, x]</nowiki></code>''' resulta [[File:Integral1.PNG]]<br>'''<code><nowiki>Integral[x³ + 3 x y, y]</nowiki></code>''' da [[File:Integral2.PNG]]<br>'''<code><nowiki>Integral[cos(3x y), y]</nowiki></code>''' da [[File:Integral3Dibujo.PNG]] | :{{Examples|1=<br>'''<code><nowiki>Integral[x³ + 3 x y, x]</nowiki></code>''' resulta [[File:Integral1.PNG]]<br>'''<code><nowiki>Integral[x³ + 3 x y, y]</nowiki></code>''' da [[File:Integral2.PNG]]<br>'''<code><nowiki>Integral[cos(3x y), y]</nowiki></code>''' da [[File:Integral3Dibujo.PNG]] | ||
}} | }} | ||
===→ Integral Definida=== | ===→ Integral Definida=== | ||
| − | ;Integral | + | ;Integral( <Función>, <Valor x<sub>Inicial</sub>>, <Valor x<sub>Final</sub>> ):Calcula el valor de la integral definida de la función en el intervalo fijado<sup>[''x<sub><small>'''inicial'''</small></sub>'', ''x<sub><small>'''final'''</small></sub>'']</sup> {{Note|1=También traza y sombrea el área entre [[Líneas y Ejes#EjeX / EjeY --- Abscisas y Ordenadas de un Punto|eje ''x'']] y el gráfico de la función ''f '' en el intervalo indicado<sup>[''abscisa<sub><small>'''inicial'''</small></sub>'', ''abscisa<sub><small>'''final'''</small></sub>'']</sup>}} |
:{{OJo|1=<br>'''<code>Integral[f, a, b]</code>''' calcula el valor de la integral definida en el intervalo [''a'', ''b''] de la función ''f'', siendo el resultado de signo contrario si en lugar de ser ''a'' < ''b'' fuera ''a'' > ''b''.}} | :{{OJo|1=<br>'''<code>Integral[f, a, b]</code>''' calcula el valor de la integral definida en el intervalo [''a'', ''b''] de la función ''f'', siendo el resultado de signo contrario si en lugar de ser ''a'' < ''b'' fuera ''a'' > ''b''.}} | ||
:{{Example|1='''<code>Integral[3y²cos(y³/3)/2,-π/4,π/2]</code>''' da ''1.68''}} | :{{Example|1='''<code>Integral[3y²cos(y³/3)/2,-π/4,π/2]</code>''' da ''1.68''}} | ||
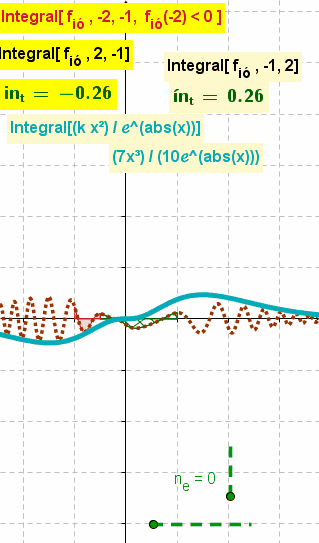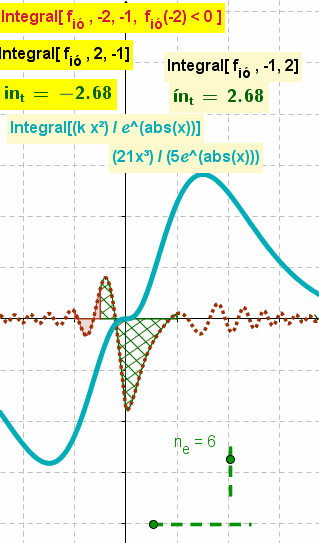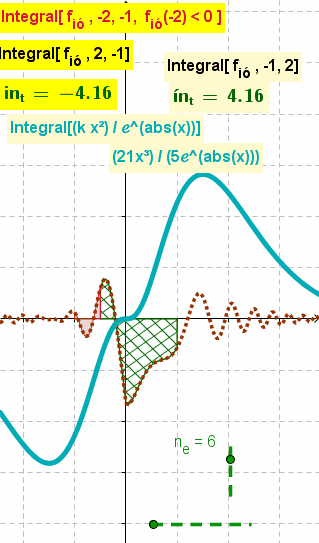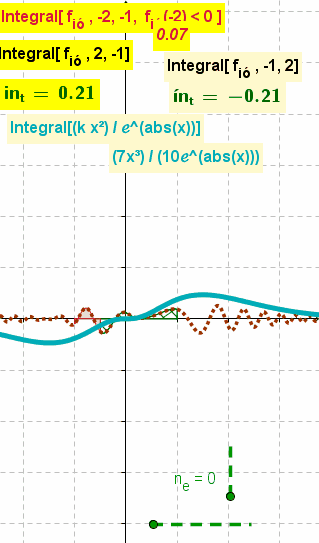
| − | ;Integral | + | ;Integral( <Función>, <Valor x Inicial>, <Valor x Final>, <Condición Booleana> ):Traza y sombrea el área entre el [[Líneas y Ejes#EjeX / EjeY --- Abscisas y Ordenadas de un Punto|eje ''x'']] y la curva de la función en el intervalo fijado<sup>[''x<sub><small>'''inicial'''</small></sub>'', ''x<sub><small>'''final'''</small></sub>'']</sup>.<br>Para una condición ''cierta''<sup>''true''</sup>, da por resultado el valor de la integral definida de la función en el intervalo<sup>[''x<sub><small>'''inicial'''</small></sub>'', ''x<sub><small>'''final'''</small></sub>'']</sup>[[File:Integrando.gif|right]] |
:{{Notes|1=<br>'''<code>Integral[f,a,b,f(a)>0]</code>''' sombrea el área entre ''f(x) '' y el intervalo [''a'', ''b''] del [[Líneas y Ejes#EjeX / EjeY --- Abscisas y Ordenadas de un Punto|eje ''x'']].<br>Para un valor ''cierto''<sup>''true''</sup> de la ''booleanba'', se establece también el valor de la integral definida de ''f(x)'' en el intervalo [''a'', ''b''].<br><br>El cálculo queda delimitado al condicionante y solo opera si lo que se evalúa resulta ''cierto''<sup>''true''</sup>. Sea la condición ''verdadera''<sup>''true''</sup> o ''falsa''<sup>''false''</sup>, queda sombreada el área correspondiente.}}<hr><small>El boceto ilustra ''animadamente'' los resultados de cada '''integral definida''' de una función que varía aleatoriamente. en el intervalo fijado <br>Puede apreciarse también el valor de la que resulta ''definida'' en el intervalo ''inverso''.<br>La tercera '''integral definida''' muestra la zona sombreada en rojo y, dependiente de una condición ''booleana'' cuyo valor de verdad varía aleatoriamente, solo exhibe el correspondiente valor calculado cuando resulta ''cierta''<sup>''true''</sup><br>La curva en celeste expone la evolución de un integral indefinida correspondiente a la primitiva que en el mismo tono resulta de la operación señalada.<hr></small> | :{{Notes|1=<br>'''<code>Integral[f,a,b,f(a)>0]</code>''' sombrea el área entre ''f(x) '' y el intervalo [''a'', ''b''] del [[Líneas y Ejes#EjeX / EjeY --- Abscisas y Ordenadas de un Punto|eje ''x'']].<br>Para un valor ''cierto''<sup>''true''</sup> de la ''booleanba'', se establece también el valor de la integral definida de ''f(x)'' en el intervalo [''a'', ''b''].<br><br>El cálculo queda delimitado al condicionante y solo opera si lo que se evalúa resulta ''cierto''<sup>''true''</sup>. Sea la condición ''verdadera''<sup>''true''</sup> o ''falsa''<sup>''false''</sup>, queda sombreada el área correspondiente.}}<hr><small>El boceto ilustra ''animadamente'' los resultados de cada '''integral definida''' de una función que varía aleatoriamente. en el intervalo fijado <br>Puede apreciarse también el valor de la que resulta ''definida'' en el intervalo ''inverso''.<br>La tercera '''integral definida''' muestra la zona sombreada en rojo y, dependiente de una condición ''booleana'' cuyo valor de verdad varía aleatoriamente, solo exhibe el correspondiente valor calculado cuando resulta ''cierta''<sup>''true''</sup><br>La curva en celeste expone la evolución de un integral indefinida correspondiente a la primitiva que en el mismo tono resulta de la operación señalada.<hr></small> | ||
===[[Image:Menu view cas.svg|link=Vista CAS|18px]] Integral Indefinida [[Comandos Específicos CAS (Cálculo Avanzado)|en]] la [[Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== | ===[[Image:Menu view cas.svg|link=Vista CAS|18px]] Integral Indefinida [[Comandos Específicos CAS (Cálculo Avanzado)|en]] la [[Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== | ||
Se obra con las variantes previas de integración definida admitiendo, además, literales para operar simbólicamente y la indicación de cualquier variable (no solo '''<code>x</code>''', '''<code>y</code>''' o '''<code>z</code>'''). | Se obra con las variantes previas de integración definida admitiendo, además, literales para operar simbólicamente y la indicación de cualquier variable (no solo '''<code>x</code>''', '''<code>y</code>''' o '''<code>z</code>'''). | ||
Aunque esto inhabilita, a su vez, la graficación:<small><center>{{Attention|1=Exclusiva de [[Vista CAS|Vista CAS]]: Se admite cualquier variable (no solo ''x'', ''y'' o ''z'')}}</center></small> | Aunque esto inhabilita, a su vez, la graficación:<small><center>{{Attention|1=Exclusiva de [[Vista CAS|Vista CAS]]: Se admite cualquier variable (no solo ''x'', ''y'' o ''z'')}}</center></small> | ||
| − | ;Integral | + | ;Integral( <Función> ):Establece la integral indefinida de la función respecto de la variable principal.<small>{{OJo|1=De presentarse diferentes variables, más allá de ''<code>x</code>'', ''<code>y</code>'' o ''<code>z</code>'', para que opere como ''principal'' la que no fuese la primera en el orden de aparición, debe optarse por indicarla como tal.<br>Si las variables en juego fueran ''<code>x</code>'', ''<code>y</code>'' o ''<code>z</code>'', solo es preciso indicar la ''principal'' si no fuese la ''primera'' alfabéticamente.}}</small> |
:{{Example|1=En la [[Vista CAS]]...<br><br>'''<code>Integral[z cos(3 y x)]</code>''' da [[File:Integral5.PNG]]}} | :{{Example|1=En la [[Vista CAS]]...<br><br>'''<code>Integral[z cos(3 y x)]</code>''' da [[File:Integral5.PNG]]}} | ||
| − | ;Integral | + | ;Integral( <Función>, <Variable> ):Establece la integral indefinida de la función respecto de la variable indicada. |
:{{Examples|1=En la [[Vista CAS]]...<br><br>'''<code>Integral[z cos(3 y x), y]</code>''' da [[File:Integrall7.PNG]]<br><br>'''<code>Integral[cos(t/ñ)]</code>''' da [[File:Integralñ.PNG]]<br><br>'''<code>Integral[cos(t ñ), ñ]</code>''' da <math>\frac{sen(t ñ)}{t}</math> + c<sub>1</sub><br><br>'''<code><nowiki>Integral[cos(3 t), t]</nowiki></code>''' da <math>\frac{1}{3}</math> sen(3t) ) + c<sub>1</sub><br>'''<code><nowiki>Integral[cos(k t), t]</nowiki></code>''' da <math>\frac{1}{k}</math> sen(k t) ) + c<sub>1</sub> | :{{Examples|1=En la [[Vista CAS]]...<br><br>'''<code>Integral[z cos(3 y x), y]</code>''' da [[File:Integrall7.PNG]]<br><br>'''<code>Integral[cos(t/ñ)]</code>''' da [[File:Integralñ.PNG]]<br><br>'''<code>Integral[cos(t ñ), ñ]</code>''' da <math>\frac{sen(t ñ)}{t}</math> + c<sub>1</sub><br><br>'''<code><nowiki>Integral[cos(3 t), t]</nowiki></code>''' da <math>\frac{1}{3}</math> sen(3t) ) + c<sub>1</sub><br>'''<code><nowiki>Integral[cos(k t), t]</nowiki></code>''' da <math>\frac{1}{k}</math> sen(k t) ) + c<sub>1</sub> | ||
}} | }} | ||
| Línea 26: | Línea 26: | ||
===[[Image:Menu view cas.svg|link=Vista CAS|18px]] Integral Definida [[Comandos Específicos CAS (Cálculo Avanzado)|en]] la [[Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== | ===[[Image:Menu view cas.svg|link=Vista CAS|18px]] Integral Definida [[Comandos Específicos CAS (Cálculo Avanzado)|en]] la [[Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== | ||
Excepto la sintaxis que incluye un valor booleano, se obra en esta [[Vista CAS|vista]] con la variante previa ampliada al admitirse literales y cualquier variable (no solo '''<code>x</code>''', '''<code>y</code>''' o '''<code>z</code>''') aunque esto inhabilita, a su vez, la graficación:<small><center>{{Attention|1=Exclusiva de [[Vista CAS|Vista CAS]]: Se admite cualquier variable (no solo ''x'', ''y'' o ''z'')}}</center></small> | Excepto la sintaxis que incluye un valor booleano, se obra en esta [[Vista CAS|vista]] con la variante previa ampliada al admitirse literales y cualquier variable (no solo '''<code>x</code>''', '''<code>y</code>''' o '''<code>z</code>''') aunque esto inhabilita, a su vez, la graficación:<small><center>{{Attention|1=Exclusiva de [[Vista CAS|Vista CAS]]: Se admite cualquier variable (no solo ''x'', ''y'' o ''z'')}}</center></small> | ||
| − | ;Integral | + | ;Integral( <Función>, <Variable>, <Valor variable Inicial>, <Valor variable Final> ):Establece la integral definida de la función respecto de la variable indicada dentro del intervalo<sup>[''valos<sub><small>'''variable<sub>inicial</sub>'''</small></sub>'', ''valor<sub><small>'''variable<sub>final</sub>'''</small></sub>'']</sup> fijado por sendos valores numéricos.<small>{{OJo|1=Todo literal admisible, más allá de '''''x''''' o '''''y''''' o '''''z''''', puede operar como ''variable'' y constituirse como tal.}}</small> |
:{{Note|1=<br>'''<code><nowiki>Integral[f, t, a, b]</nowiki></code>''' establece la integral definida de la función ''f'' respecto de la variable ''t'' dentro del intervalo entre ''a'' y ''b''}} | :{{Note|1=<br>'''<code><nowiki>Integral[f, t, a, b]</nowiki></code>''' establece la integral definida de la función ''f'' respecto de la variable ''t'' dentro del intervalo entre ''a'' y ''b''}} | ||
:{{Examples|1=<br>'''<code><nowiki>Integral[cos(3 t), t]</nowiki></code>''' da <math>\frac{1}{3}</math> sen(3 t) + c<sub>1</sub><br>'''<code><nowiki>Integral[cos(k t),t,ñ,ñ+1]</nowiki></code>''' da por resultado ''<math> \frac{sen(k ñ + k) - sen(k ñ)}{k}</math>'' | :{{Examples|1=<br>'''<code><nowiki>Integral[cos(3 t), t]</nowiki></code>''' da <math>\frac{1}{3}</math> sen(3 t) + c<sub>1</sub><br>'''<code><nowiki>Integral[cos(k t),t,ñ,ñ+1]</nowiki></code>''' da por resultado ''<math> \frac{sen(k ñ + k) - sen(k ñ)}{k}</math>'' | ||
Revisión del 20:03 8 oct 2017
Integral
Categorías de Comandos (todos)
→ Integral Indefinida / Primitiva
- Integral( <Función> )
- Establece y grafica la primitiva de la función respecto de la variable principal.
- }
- Integral( <Función>, <Variable> )
- Establece la integral indefinida parcial de la función respecto de la variable indicada.
 Atención: Desde la Barra de Entrada solo se puede indicar como variable
Atención: Desde la Barra de Entrada solo se puede indicar como variable xoyozde una eventual función multivariable dada.
→ Integral Definida
- Integral( <Función>, <Valor xInicial>, <Valor xFinal> )
- Calcula el valor de la integral definida de la función en el intervalo fijado[xinicial, xfinal] Nota: También traza y sombrea el área entre eje x y el gráfico de la función f en el intervalo indicado[abscisainicial, abscisafinal]
 Atención:
Atención: Integral[f, a, b]calcula el valor de la integral definida en el intervalo [a, b] de la función f, siendo el resultado de signo contrario si en lugar de ser a < b fuera a > b.
- Ejemplo:
Integral[3y²cos(y³/3)/2,-π/4,π/2]da 1.68 - Integral( <Función>, <Valor x Inicial>, <Valor x Final>, <Condición Booleana> )
- Traza y sombrea el área entre el eje x y la curva de la función en el intervalo fijado[xinicial, xfinal].
Para una condición ciertatrue, da por resultado el valor de la integral definida de la función en el intervalo[xinicial, xfinal] - Notas:
Integral[f,a,b,f(a)>0]sombrea el área entre f(x) y el intervalo [a, b] del eje x.
Para un valor ciertotrue de la booleanba, se establece también el valor de la integral definida de f(x) en el intervalo [a, b].
El cálculo queda delimitado al condicionante y solo opera si lo que se evalúa resulta ciertotrue. Sea la condición verdaderatrue o falsafalse, queda sombreada el área correspondiente.
El boceto ilustra animadamente los resultados de cada integral definida de una función que varía aleatoriamente. en el intervalo fijado
Puede apreciarse también el valor de la que resulta definida en el intervalo inverso.
La tercera integral definida muestra la zona sombreada en rojo y, dependiente de una condición booleana cuyo valor de verdad varía aleatoriamente, solo exhibe el correspondiente valor calculado cuando resulta ciertatrue
La curva en celeste expone la evolución de un integral indefinida correspondiente a la primitiva que en el mismo tono resulta de la operación señalada.
 Integral Indefinida en la Vista ComputaciónAlgebraicaSimbólica
Integral Indefinida en la Vista ComputaciónAlgebraicaSimbólica
Se obra con las variantes previas de integración definida admitiendo, además, literales para operar simbólicamente y la indicación de cualquier variable (no solo x, y o z).
Aunque esto inhabilita, a su vez, la graficación:
| Exclusiva de Vista CAS: Se admite cualquier variable (no solo x, y o z) |
- Integral( <Función> )
- Establece la integral indefinida de la función respecto de la variable principal.
 Atención: De presentarse diferentes variables, más allá de
Atención: De presentarse diferentes variables, más allá de x,yoz, para que opere como principal la que no fuese la primera en el orden de aparición, debe optarse por indicarla como tal.
Si las variables en juego fueranx,yoz, solo es preciso indicar la principal si no fuese la primera alfabéticamente.
- Integral( <Función>, <Variable> )
- Establece la integral indefinida de la función respecto de la variable indicada.
- Ejemplos: En la Vista CAS...
Integral[z cos(3 y x), y]daIntegral[cos(t/ñ)]daIntegral[cos(t ñ), ñ]da \frac{sen(t ñ)}{t} + c1Integral[cos(3 t), t]da \frac{1}{3} sen(3t) ) + c1Integral[cos(k t), t]da \frac{1}{k} sen(k t) ) + c1
 Integral Definida en la Vista ComputaciónAlgebraicaSimbólica
Integral Definida en la Vista ComputaciónAlgebraicaSimbólica
Excepto la sintaxis que incluye un valor booleano, se obra en esta vista con la variante previa ampliada al admitirse literales y cualquier variable (no solo x, y o z) aunque esto inhabilita, a su vez, la graficación:
| Exclusiva de Vista CAS: Se admite cualquier variable (no solo x, y o z) |
- Integral( <Función>, <Variable>, <Valor variable Inicial>, <Valor variable Final> )
- Establece la integral definida de la función respecto de la variable indicada dentro del intervalo[valosvariableinicial, valorvariablefinal] fijado por sendos valores numéricos.
 Atención: Todo literal admisible, más allá de x o y o z, puede operar como variable y constituirse como tal.
Atención: Todo literal admisible, más allá de x o y o z, puede operar como variable y constituirse como tal.
- Nota:
Integral[f, t, a, b]establece la integral definida de la función f respecto de la variable t dentro del intervalo entre a y b - Ejemplos:
Integral[cos(3 t), t]da \frac{1}{3} sen(3 t) + c1Integral[cos(k t),t,ñ,ñ+1]da por resultado \frac{sen(k ñ + k) - sen(k ñ)}{k}
 Idea: → La primitiva se anula en a así como su representación
Idea: → La primitiva se anula en a así como su representación- Ejemplo:
f(x):=x²F(x):=Integral[f,2,x]- crea F(x):= \frac{1}{3} x^3 -\frac{8}{3} la primitiva que se anula en x=2
Nota: Ver también los siguientes comandos: