Comando Baricentro

Baricentro

Categorías de Comandos (todos)

• 3D
• Álgebra
• CAS
• Cónica
• Diagrama
• Discreta
• Estadísticas
• Financieros
• Funciones y Cálculo
• GeoGebra
• Geometría
  • ArcoCircunferencia
  • Punto
  • PuntoMedio
  • Recta
  • Segmento
  • Semirrecta
  • ... y otros
• Guion (scripting)
• Hoja de Cálculo
• Lista
• Lógica
• Optimización
• Probabilidad
• Texto
• Transformación
• Vector y Matriz

Baricentro[ <Polígono> ]

Establece el baricentro o centroide del polígono, que se asocia a su isobaricentro e idealmente coincide con su centro de gravedad.

Alerta:

No confundir con el caso general en que el centro de gravedad de un polígono o el baricentro del sistema discreto de puntos de masa queda constituido por sus vértices.

Ejemplo:

Dados los puntos A = (1, 4), B = (1, 1), C = (5, 1) y D = (5, 4) los vértices de un polígono. pol := Polígono[ A, B, C, D ] grafica y registra en la Vista Algebraica a pol = 12. Baricentro[ pol ] con un Baricentro O = (3, 2.5).

---

Sea un polígono convexo, determinado por sus n vértices, ordenados
(x_{0},y_{0}), (x_{1},y_{1}), (x_{2},y_{2}), . . . (x_{n-1},y_{n-1})

Su área puede establecerse con la siguiente formulación algebraica:

\mathcal{A} = \frac{1}{2} \displaystyle\sum_{i=0}^{n-1} {(x_{i} y_{i+1} - x_{i+1} y_{i})}
(en una notación "rápida" en la que se sobre-entiende que (x_{n}, y_{n}) est (x_{0}, y_{0}).)

Las coordenadas de su centro de gravedad G están dadas por:

G_{x} = \frac{1}{6 \mathcal{A}}\displaystyle \sum_{i=0}^{n-1} {(x_{i} + x_{i+1})(x_{i} y_{i+1} - x_{i+1} y_{i})}

G_{y} = \frac{1}{6 \mathcal{A}} \displaystyle\sum_{i=0}^{n-1} {(y_{i} + y_{i+1})(x_{i} y_{i+1} - x_{i+1} y_{i})}

Atención: En cambio, hay igualdad para triángulos, paralelogramos y polígonos regulares.

---

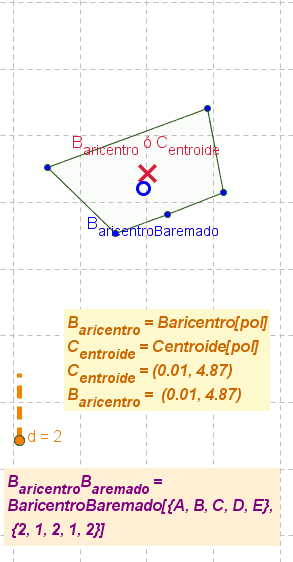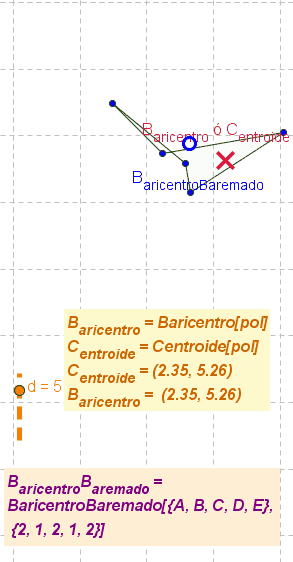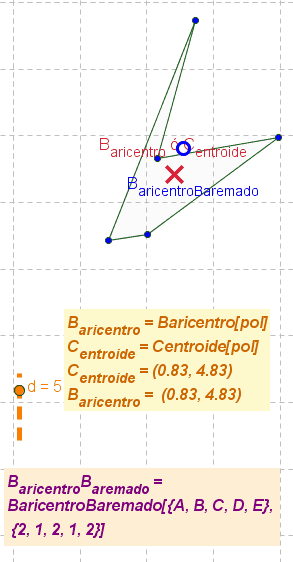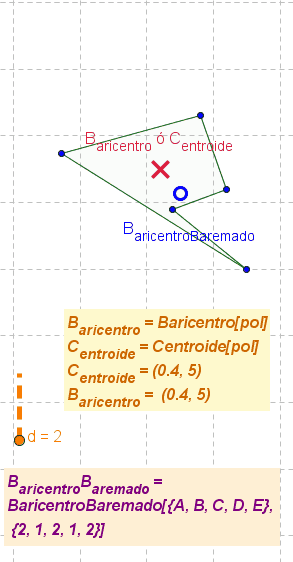
Nota: El boceto ilustra animadamente el cambio de posición del baricentro o centroide y del baricentro baremado a medida que se modifica el polígono y los pesos de cada uno de sus vértices.

---

Atención: Puede consultarse al respecto el archivo geogebratube