Puntos y Vectores

Sobre Puntos y Vectores
Ingreso de Puntos y Vectores
Los puntos y vectores pueden ingresarse en la Barra de Entrada, en coordenada cartesianas (el separador es la coma), polares o esféricas (el separador es el punto y coma).
Los puntos, también pueden crearse con herramientas como...
- la de
 Punto
Punto - la de vector
 Equipolente
Equipolente - o la de
 Vector
Vector
... y con una variedad de comandos.
Para ingresar un punto, se anota...
P = (1, 0)para crear P en coordenadas cartesianas y...v = (0, 5)si se tratara de un vector, como v
P = (1; 0°)en coordenadas polares y...v = (5; 90°)si se tratara de un vector, como v
El menú contextual de un punto (o de un vector) del plano se puede alternar entre la representación Coordenadas cartesienas <> Coordenadas polares. Las lecturas de las coordenadas de un punto A (por ejemplo) del plano se conforma por:
- x(A) e y(A) para las coordenadas cartesianas,
- Longitud(A) y Ángulo(A) para las coordenadas polares.
- Longitud(A) , arg(A) y alt(A) ara las coordenadas esféricas. (Debe considerarse que el Ángulo[A], da por resultado siempre el ángulo (Ox,OA))
Para ubicarlos en la Hoja de Cálculo, de modo que se los identifique y nombre según la dirección de la celda de cabida, se anota...
A2 = (1, 0)para ubicarlo en coordenadas cartesianas en la celda (A2 en este caso)A2 = (1; 10°)operando en polares
El separador de las coordenadas polares es el punto y coma.
Si no se anota el símbolo de grados, GeoGebra asume que el valor del ángulo se expresa en radianes.
Se puede acceder a las coordenadas de un punto, como Q anotando....
abs(Q)yarg(Q)para sendos componentes de las coordenadas polaresx(Q)yy(Q)para cartesianas del punto Q, con las mismas funciones predefinidas x e y si se trata de vectores.
P=(1, 2) es un punto y v=(3, 4) un vector,x(P) da por resultado 1 y y(v), 4.Puntos
Cálculos Puntuales
- Puntos
Un punto puede quedar definido desde la Barra o Campo de Entrada por sus tres coordenadas
- Cartesianas
- Esféricas
- Por tres coordenadas cartesianas
- C=(1,2,3)
- Por tres coordenadas esféricas
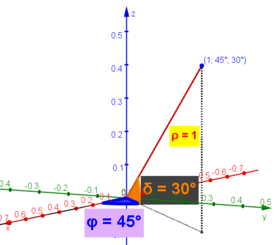
- A=(1 ; 45°;30°)
- (ρ, φ, δ) donde...
- ρ designa la distancia del punto al origen,
- φ designa la longitud (ángulo polar de la proyección del objeto sobre xOy, medido tras el eje x, entre 0° y 360°)
- δ la latitud, el ángulo tras el plano xOy (entre -90° y 90°)
Ilustrando con Coordenadas
Sobre Vectores
Vectores
En GeoGebra, pueden hacerse cálculos con puntos y vectores.
Puede establecerse...
- el punto medio M entre A y B anotando, en la Barra de Entrada:
M = (A + B) / 2
- la longitud de un vector v con
longitud = sqrt(v * v)
Se puede operar con un punto, como A, para establecer otro. Así...
- Siendo A = (a, b), A + 1 crea otro punto, B, de coordenadas (a + 1, b + 1)
- Siendo A un número complejo a + b i, entonces...
- A + 1 crea otro, el número complejo a+1+bi y
- A + i, el número complejo a+ (b + 1) i
Versión Previa
Categorías de Comandos (todos)
Producto Vectorial
Para dos puntos o dos vectores (a, b)⊗(c, d) da por resultado la coordenada-z del producto vectorial (a, b, 0)⊗(c, d, 0) como un simple número.
Similar sintaxis es válida para listas pero el resultado en tal caso, es una lista.
{1, 2} ⊗ {4, 5}da por resultado {0, 0, -3}{1, 2, 3} ⊗ {4, 5, 6}da {3, 6, -3} dado que el producto vectorial usual opera con listas.
- ProductoVectorial( <Vector> , <Vector> )
- Calcula el producto vectorial (cross product en inglés) de un vector por el otro, expresándolo como una lista.
Así, ProductoVectorial(<Vector\vec{u}>, <Vector\vec{v}> ) siendo \vec{u} = \begin{pmatrix}a \\ b\end{pmatrix} y \vec{v} = \begin{pmatrix}c \\ d\end{pmatrix} dos vectores del plano, establece el determinante bi-vectorial o calcula el producto vectorial de (a,b,0) y (c,d,0).
En ámbitos 3D, además puede representar el resultado.
Dados dos vectores en el plano \vec{u} = \begin{pmatrix}2 \\ 2\end{pmatrix} y \vec{v} = \begin{pmatrix}-3 \\ 1\end{pmatrix}
ProductoVectorial(u, v) da el número 8 (2 x 1 - 2 x -3).(El determinante del bi-vector del producto vectorial de (2,2,0) y (-3,1,0)).
Dados dos vectores en el espacio \vec{u} y \vec{v} (como lista de 3 elementos), se puede obtener el correspondiente resultante del producto vectorial de ambos como lista de 3 elementos. Así:
ProductoVectorial({1, 3, 2}, {0, 3, -2}) da por resultado la lista {-12, 2, 3}, el producto vectorial de {1, 2, 3} por {0, 3, -2}, correspondiente al vector \left( \begin{array}{} -12 \\ 2 \\ 3 \end{array} \right) que es el producto vectorial de \left( \begin{array}{} 1 \\ 3 \\ 2 \end{array} \right) y de \begin{pmatrix}0 \\ 3\\-2\end{pmatrix} .En la Barra de Entrada puede usarse el operador correspondiente, anotando, por ejemplo,
u ⊗ v En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
En esta vista se admiten literales para operar simbólicamente
| Si en uno u otro vector hubiera variables sin valor asignado, resulta la fórmula correspondiente. |
ProductoVectorial({a, b, c}, {d, e, f}) da {b f - c e, -a f + c d, a e - b d}ProductoVectorial({a, b}, {c, d}) da {0, 0, a d - b c}Sobre Matrices
Matrices
GeoGebra también opera con matrices, representadas como una lista de listas, que contiene las filas de la matriz.
a = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} representa la matriz a de 3x3:
FórmulaTexto({{1, 2, 3}, {4, 5, 6}, {7, 8, 9} }) para exponer la matriz usando formato LaTeX.Esta categoría no contiene ninguna página o archivo.