Diferencia entre revisiones de «Categoría:Objetos Generales»

m (link) |
m (link) |
||
| Línea 1: | Línea 1: | ||
| − | <small>{{Objects|generales}}{{DISPLAYTITLE:Objetos Generales Categorizados}}</small>Además de operar sobre [[Objetos Geométricos]], GeoGebra también puede manejar:<br> | + | <small>{{Objects|generales}}{{DISPLAYTITLE:Objetos Generales Categorizados}}</small>Además de operar sobre [[:Categoría:Objetos Geométricos|Objetos Geométricos]], GeoGebra también puede manejar:<br> |
:[[Números y Ángulos]] | :[[Números y Ángulos]] | ||
:[[Números complejos|Números complejos]] | :[[Números complejos|Números complejos]] | ||
| Línea 10: | Línea 10: | ||
==Objetos de todo Tipo== | ==Objetos de todo Tipo== | ||
'''GeoGebra''' permite operar diversidades de ''objetos'' que admiten diferentes registros y ''vistas'' y pueden clasificarse según su tipo: | '''GeoGebra''' permite operar diversidades de ''objetos'' que admiten diferentes registros y ''vistas'' y pueden clasificarse según su tipo: | ||
| − | *[[Objetos Geométricos]] | + | *[[:Categoría:Objetos Geométricos|Objetos Geométricos]] |
*Objetos Generales | *Objetos Generales | ||
*[[:Categoría:Objetos_de_Acción|Objetos de Acción]] | *[[:Categoría:Objetos_de_Acción|Objetos de Acción]] | ||
| Línea 20: | Línea 20: | ||
===Geométricos y Diversos=== | ===Geométricos y Diversos=== | ||
GeoGebra trabaja con diversos tipos de objetos geométricos que pueden operar dentro de otras modalidades como, por ejemplo: | GeoGebra trabaja con diversos tipos de objetos geométricos que pueden operar dentro de otras modalidades como, por ejemplo: | ||
| − | *[[:Categoría:Objetos_Geométricos# | + | *[[:Categoría:Objetos_Geométricos#Funciones|Funciones]] |
| − | *[[Curvas]] | + | *[[:Categoría:Curvas|Curvas]] |
*[[Inecuaciones|Desigualdades e Inecuaciones]] | *[[Inecuaciones|Desigualdades e Inecuaciones]] | ||
*[[Intervalos]] | *[[Intervalos]] | ||
===Acciones sobre Objetos=== | ===Acciones sobre Objetos=== | ||
| − | Los más ''salientes'' son los [[Objetos Geométricos]] y los que se articulan con operaciones son los [[:Categoría:Objetos_de_Acción|Objetos de Acción]]. Además, se admiten los de otros estilos, ya mencionados. | + | Los más ''salientes'' son los [[:Categoría:Objetos Geométricos|Objetos Geométricos]] y los que se articulan con operaciones son los [[:Categoría:Objetos_de_Acción|Objetos de Acción]]. Además, se admiten los de otros estilos, ya mencionados. |
[[Category:Objetos]] | [[Category:Objetos]] | ||
<!--Typesd’objets généraux reconnus par GeoGebra<br>[[Nombres et Angles]]<br>[[Nombres complexes]]<br>[[Valeurs booléennes]]<br>[[Listes]]<br>[[Matrices]]<br>[[Textes]] [[fr:Catégorie:Généraux]]--> | <!--Typesd’objets généraux reconnus par GeoGebra<br>[[Nombres et Angles]]<br>[[Nombres complexes]]<br>[[Valeurs booléennes]]<br>[[Listes]]<br>[[Matrices]]<br>[[Textes]] [[fr:Catégorie:Généraux]]--> | ||
Revisión del 02:43 15 feb 2020
Además de operar sobre Objetos Geométricos, GeoGebra también puede manejar:
Objetos de todo Tipo
GeoGebra permite operar diversidades de objetos que admiten diferentes registros y vistas y pueden clasificarse según su tipo:
- Objetos Geométricos
- Objetos Generales
- Objetos de Acción
- Caracterizados según sus Propiedades
- Clasificados acorde a su Estilo
- Nombrados y Determinados por Operaciones Diversas
- Calificados como Avanzados
- Programas (guion-scripting)
Geométricos y Diversos
GeoGebra trabaja con diversos tipos de objetos geométricos que pueden operar dentro de otras modalidades como, por ejemplo:
Acciones sobre Objetos
Los más salientes son los Objetos Geométricos y los que se articulan con operaciones son los Objetos de Acción. Además, se admiten los de otros estilos, ya mencionados.
Matrices
Una lista de listas supone en GeoGebra una matriz.
Sobre Matrices
GeoGebra también opera con matrices reales, representadas como una lista de listas, que contiene las filas de la matriz.
a = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} representa la matriz a de 3x3:
FórmulaTexto[{{1, 2, 3}, {4, 5, 6}, {7, 8, 9} }] para exponer la matriz usando formato LaTeX.Operaciones con Matrices
Sumas y Restas - Ejemplos
- Matriz1 + Matriz2: Suma uno a uno, cada par de elementos correspondientes de una y otra matriz.
- Matriz1 – Matriz2: Resta uno a uno, cada par de elementos correspondientes de una y otra matriz, entre dos compatibles entre sí.
Multiplicación - Ejemplos
- Matriz * Número: Multiplica por el número, cada uno de los elementos de la matriz.
- Matriz1 * Matriz2: Usa la multiplicación de matrices para calcular la resultante.
- Nota: Las filas de la primera y las columnas de la segunda matriz deben tener el mismo número de elementos.
- Ejemplo: {{1,2},{3,4},{5,6}}*{{1,2,3},{4,5,6}} da por resultado la matriz {{9, 12, 15}, {19, 26, 33}, {29, 40, 51}}.
- 2x2 Matriz * Punto (o Vector): Multiplica la matriz por el punto o vector y da por resultado un punto
- 3x3 Matriz * Punto (o Vector): Multiplica la matriz por el punto o vector y da por resultado un punto.
- Ejemplos:
- {{1, 2}, {3, 4}, {5, 6}} * {{1, 2, 3}, {4, 5, 6}} da por resultado la matriz {{9, 12, 15}, {19, 26, 33}, {29, 40, 51}}
- {{1, 2}, {3, 4}} * (3, 4) da por resultado el punto A = (11, 25).
- {{1, 2, 3}, {4, 5, 6}, {0, 0, 1}} * (1, 2) da por resultado el punto A = (8, 20).
- Nota: Este es un caso especial de transformaciones afines donde las coordenadas homogéneas se usan: (x, y, 1) para un punto y (x, y, 0) por un vector. Este último ejemplo es, por lo tanto, equivalente a:
{{1, 2, 3}, {4, 5, 6}, {0, 0, 1}} * {1, 2, 1}.
| Para dividir la matriz_A por la matriz_B, no se apela a A/B sino a A*Inversa[B] o A*B^(-1).
Dadas las matrices matriz_A = {{6, 2, 3}, {4, 5, 6}, {9, 8, 14}} matriz_A*Inversa[matriz_B] o matriz_A matriz_B^(-1) que da la matriz:\left(\begin{array}{}-1&-6&5\\-1&7&0\\-6&6&7\\ \end{array}\right) |
Profundizando
Comandando con Matrices
Objetos Generales
Categorías de Comandos (todos)
- DiagonalizaciónJordan( <Matriz> )
- Devuelve la descomposición de la matriz según la forma canónica de Jordan en una lista de un par de matrices P y J tal que A = P*J*P-1 (J está expresada en la forma canónica de Jordan)
Ejemplos y Variantes
DiagonalizaciónJordan({{1, 2}, {3, 4}})devuelve \left(\begin{array}{}\sqrt{33} - 3&-\sqrt{33} - 3\\6&6\\\end{array}\right) , \left(\begin{array}{}\frac{\sqrt{33} + 5}{2}&0\\0&\frac{-\sqrt{33} + 5}{2}\\\end{array}\right)- Siendo A:= \left(\begin{array}{}-1&-1&0&0\\0&-1&0&0\\0&2&0&-1\\0&-2&2&3\\\end{array}\right)
DiagonalizaciónJordan( A )
devuelve la lista de dos matrices (P = ) \left(\begin{array}{}0&0&-6&5\\0&0&0&6\\-1&-1&0&-6\\2&1&0&6\\\end{array}\right) y (J = ) \left(\begin{array}{}2&0&0&0\\0&1&0&0\\0&0&-1&1\\0&0&0&-1\\\end{array}\right) .
Ver también...
... cada uno de los siguientes comandos:
- Determinante[Matriz]: Calcula el determinante de la matriz dada.
- Inversa[Matriz]: Invierte la matriz dada.
- Traspone[Matriz]: Traspone la matriz dada.
- AplicaMatriz[Matriz, Objeto]: Aplica la transformación afín propio de la matriz al objeto.
- EscalonadaReducida[Matriz]: Convierte la matriz a la forma reducida escalonada por fila.
Interacción Algebra <=> Hoja de Cálculos
Tablas y Matrices
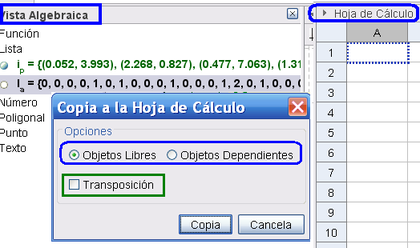
A => HC : Una matriz algebraica, puede incorporarse en la Hoja de Cálculo arrastrándola hacia allí mientras se pulsa la tecla Ctrl.
Si se establece dependiente , todo cambio en la matriz de partida repercutirá en la incrustada en la Hoja de Cálculo, dinámicamente. Para que esto no ocurra, se la debe establecer como Objeto Libre
Se puede copiar la Transposición de la matriz original.
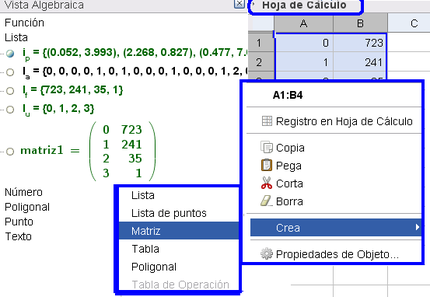
HC => A: Todo rango rectangular de celdas seleccionado en la Hoja de Cálculo, tras optar por la alternativa Crea > Matriz del Menú Contextual desplegado por un clic derecho, la registra como objeto dinámicamente dependiente. De este modo, cualquier cambio en el rango de celdas original de la hoja de cálculo, se refleja en la matriz.
Siendo l_a :=
Secuencia[BinomialAleatorio[3, 0.1], ñ, 1, 1000, Mínimo[Máximo[AleatorioEntre[1, exF], 1], 1]] la lista de registro algebraico, copiando a la Hoja de Cálculo, sendas listas lo y lf definidas como:lo :=
Ordena[Único[la]] y lf := Zip[CuentaSi[x ≟ ñ, l_a], ñ, {0,1,2,3}], cundo se selecciona el rango de celdas en que se volcaron ambas listas y se crea la correspondiente matriz, se obtiene una dinámica y aleatoriamente cambiante con cada pulsación de F9Subcategorías
Esta categoría contiene las siguientes 2 subcategorías, de un total de 2.
Páginas en la categoría «Objetos Generales»
Las siguientes 9 páginas pertenecen a esta categoría, de un total de 9.