Diferencia entre revisiones de «Categoría:Comandos de Álgebra»

De GeoGebra Manual
(link) |
m (Revertidos los cambios de LailaTov (disc.) a la última edición de LilianaSaid) |
||
| Línea 37: | Línea 37: | ||
:{{Note|1=El artículo que ilustra cómo se [[:w:es:Completando_el_cuadrado| ''completa el cuadrado'']]] (en inglés [[w:Completing_the_square|''completing the square'']]) muestra cómo esta maniobra y modalidad puede resultar útil para describir y graficar funciones cuadráticas, una vez que se las establece con la forma: ;<math>a(x-h)^2+k</math>}}</small> | :{{Note|1=El artículo que ilustra cómo se [[:w:es:Completando_el_cuadrado| ''completa el cuadrado'']]] (en inglés [[w:Completing_the_square|''completing the square'']]) muestra cómo esta maniobra y modalidad puede resultar útil para describir y graficar funciones cuadráticas, una vez que se las establece con la forma: ;<math>a(x-h)^2+k</math>}}</small> | ||
[[File:Completa 1b.gif|link=|210px|center]] | [[File:Completa 1b.gif|link=|210px|center]] | ||
| − | ===[[Image:Menu view cas.svg|link=|18px]] [[ | + | ===[[Image:Menu view cas.svg|link=|18px]] [[:Categoría:Comandos Específicos CAS (Cálculo Avanzado)|En]] la [[:Categoría:Comandos Específicos CAS (Cálculo Avanzado)#Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== |
El comando obra de modo análogo al descripto, con mayor precisión en la presentación de la formulación. Admite literales en operaciones simbólicas. | El comando obra de modo análogo al descripto, con mayor precisión en la presentación de la formulación. Admite literales en operaciones simbólicas. | ||
:{{Examples|1=<br><br>'''<code>CompletaCuadrado(2x²+7x-15)</code>''' da por resultado:<br><br><big>''<math>2 </math>(x + <math>\frac{7}{4}</math>)² - <math>\frac{169}{8}</math>''</big><br><br>'''<code>CompletaCuadrado( (x + ñ)(x - ñ) + sqrt(7) x)</code>''' da por resultado:<br><br><small></small> <big><math>{ \left( x + \frac{\sqrt{7} }{2} \right)^{2} + \frac{-4 ñ^{2} - 7}{4} }</math></big> <br>}}<hr> | :{{Examples|1=<br><br>'''<code>CompletaCuadrado(2x²+7x-15)</code>''' da por resultado:<br><br><big>''<math>2 </math>(x + <math>\frac{7}{4}</math>)² - <math>\frac{169}{8}</math>''</big><br><br>'''<code>CompletaCuadrado( (x + ñ)(x - ñ) + sqrt(7) x)</code>''' da por resultado:<br><br><small></small> <big><math>{ \left( x + \frac{\sqrt{7} }{2} \right)^{2} + \frac{-4 ñ^{2} - 7}{4} }</math></big> <br>}}<hr> | ||
| Línea 47: | Línea 47: | ||
{{command|cas=true|probability|nPr|Npr|UY_version=NúmeroArreglos|non-UY_version=nPr}};nPr( <Número (o valor numérico)<sub>''n''</sub>>, <Número (o valor numérico)<sub>''p''</sub>> ):Da por resultado el número de arreglos de ''p'' elementos tomados de un conjunto de ''n'', en variaciones sin repetición.{{OJo|1=Número asociado al de variaciones [[:w:es:Combinatoria|sin repetición]], le suele corresponder en algunas calculadoras la tecla {{KeyCode|nPr}} <small></small>lo que se formula como <math>P_r^n</math><!-- o <math>\n\choose p</math>-->}} | {{command|cas=true|probability|nPr|Npr|UY_version=NúmeroArreglos|non-UY_version=nPr}};nPr( <Número (o valor numérico)<sub>''n''</sub>>, <Número (o valor numérico)<sub>''p''</sub>> ):Da por resultado el número de arreglos de ''p'' elementos tomados de un conjunto de ''n'', en variaciones sin repetición.{{OJo|1=Número asociado al de variaciones [[:w:es:Combinatoria|sin repetición]], le suele corresponder en algunas calculadoras la tecla {{KeyCode|nPr}} <small></small>lo que se formula como <math>P_r^n</math><!-- o <math>\n\choose p</math>-->}} | ||
:{{example|1=<br>'''<code>nPr(10, 2)</code>''' da ''90''.}} | :{{example|1=<br>'''<code>nPr(10, 2)</code>''' da ''90''.}} | ||
| − | ===[[Image:Menu view cas.svg|link= | + | ===[[Image:Menu view cas.svg|link=:Categoría:Comandos Específicos CAS (Cálculo Avanzado)#Vista CAS|16px]] [[:Categoría:Comandos Específicos CAS (Cálculo Avanzado)##Vista CAS|En]] la [[:Categoría:Comandos Específicos CAS (Cálculo Avanzado)#Vista CAS|Vista C<sub><small>omputación</small></sub>A<sub><small>lgebraica</small></sub>S<sub><small>imbólica</small></sub>]]=== |
| − | En esta [[ | + | En esta [[:Categoría:Comandos Específicos CAS (Cálculo Avanzado)#Vista CAS|vista]] se admite la misma sintaxis y la inclusión de literales para operar simbólicamente. |
:{{examples|1=<br>'''<code>nPr(n, 3)</code>''' es [[Herramienta de Evalúa|evaluado]] como [[Archivo:Mode evaluate.png|32px]]''n³ - 3 n² + 2 n''<br><math>{\frac{\Gamma \left( n + 1 \right)}{\Gamma \left( n - 2 \right)} }</math><br>'''<code>nPr(n, k)</code>''' al [[Herramienta de Evalúa|ser evaluado]] resulta [[Archivo:Mode evaluate.png|32px]] <math>{\frac{\Gamma \left( n + 1 \right) }{\Gamma \left( -k + n + 1 \right) } }</math><br>Siendo <math>\Gamma \left( n + 1 \right) = n!</math> equivale a <math>\frac{n!}{(n - k)! }</math><!-- </small>--> | :{{examples|1=<br>'''<code>nPr(n, 3)</code>''' es [[Herramienta de Evalúa|evaluado]] como [[Archivo:Mode evaluate.png|32px]]''n³ - 3 n² + 2 n''<br><math>{\frac{\Gamma \left( n + 1 \right)}{\Gamma \left( n - 2 \right)} }</math><br>'''<code>nPr(n, k)</code>''' al [[Herramienta de Evalúa|ser evaluado]] resulta [[Archivo:Mode evaluate.png|32px]] <math>{\frac{\Gamma \left( n + 1 \right) }{\Gamma \left( -k + n + 1 \right) } }</math><br>Siendo <math>\Gamma \left( n + 1 \right) = n!</math> equivale a <math>\frac{n!}{(n - k)! }</math><!-- </small>--> | ||
}} | }} | ||
Revisión del 21:50 12 ago 2020
Este es un artículo sobre comandos de GeoGebra
Comandos de Álgebra
Categorías de Comandos (todos)
Comandos de Álgebra
- ABase4.2
- Cociente
- CompletaCuadrado4.2
- ComúnDenominador4.2
- Desarrolla
- DesdeBase4.2
- División4.2
- Divisores4.2
- Eliminación5.0
- EsPrimo4.2
- FactoresPrimos
- Factoriza
- FactorizaI4.2
- ListaDivisores4.2
- MCD
- MCM
- Máximo
- Mínimo
- nCr
- PrimerMiembro4.2
- PrimoAnterior4.2
- PrimoSiguiente4.2
- ProductoEscalarCAS
- Resto
- SegundoMiembro4.2
- Simplifica
- SumaDivisores4.2
- Desde la versión 4.2, se cuenta con las siguientes funciones
- parteFraccionaria() (el comando pasó a ser función)
- real() pasó a ser función real()
Comando CompletaCuadrado
- CompletaCuadrado( <Función Cuadrática> )
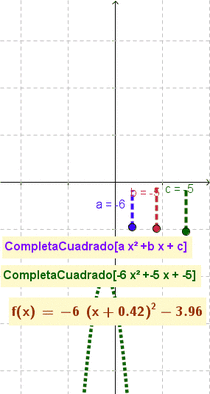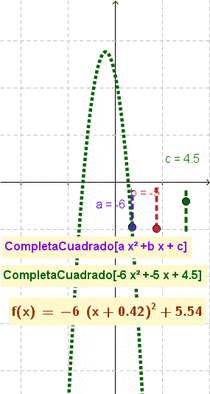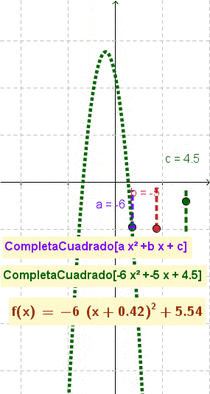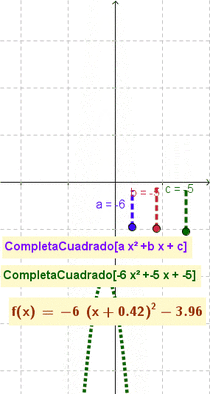
- Da por resultado y grafica la función cuadrática indicada acorde al correspondiente formato canónico a(x-h)^2+k
- Ejemplos:
CompletaCuadrado(2x²+7x-15)da por resultado 2 (x + 1.75)² - 21.125 (Opción a 3 decimales)CompletaCuadrado(x^2 - 4x + 7)crea la función (x - 2)2 + 3
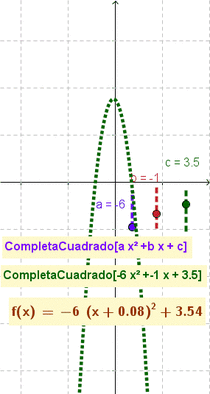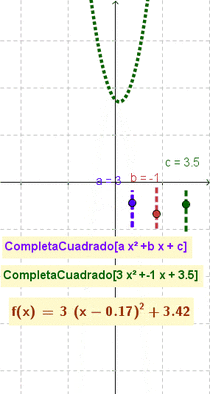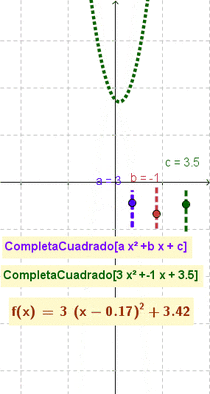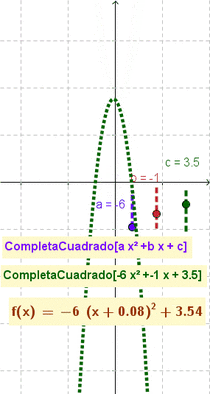
- Nota: El artículo que ilustra cómo se completa el cuadrado] (en inglés completing the square) muestra cómo esta maniobra y modalidad puede resultar útil para describir y graficar funciones cuadráticas, una vez que se las establece con la forma: ;a(x-h)^2+k
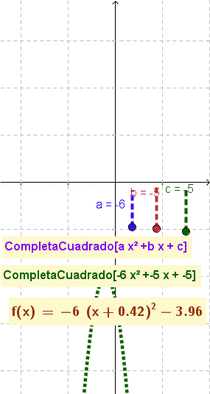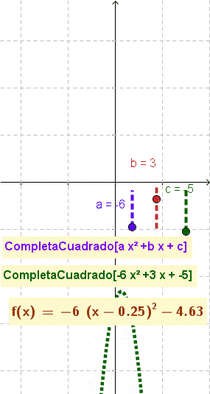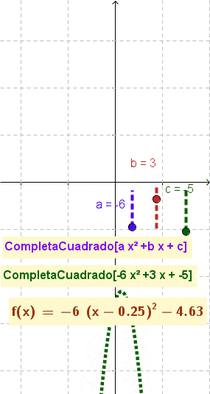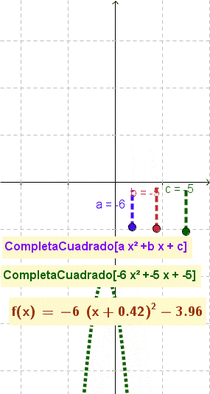
 En la Vista ComputaciónAlgebraicaSimbólica
En la Vista ComputaciónAlgebraicaSimbólica
El comando obra de modo análogo al descripto, con mayor precisión en la presentación de la formulación. Admite literales en operaciones simbólicas.
- Ejemplos:
CompletaCuadrado(2x²+7x-15)da por resultado:
2 (x + \frac{7}{4})² - \frac{169}{8}CompletaCuadrado( (x + ñ)(x - ñ) + sqrt(7) x)da por resultado:
{ \left( x + \frac{\sqrt{7} }{2} \right)^{2} + \frac{-4 ñ^{2} - 7}{4} }
- Nota: Ver también los comandos Desarrolla y Simplifica.
Comando nPr
s de Álgebra
Categorías de Comandos (todos)
Las variantes del nombre del comando en español son:
|
- nPr( <Número (o valor numérico)n>, <Número (o valor numérico)p> )
- Da por resultado el número de arreglos de p elementos tomados de un conjunto de n, en variaciones sin repetición.
 Atención: Número asociado al de variaciones sin repetición, le suele corresponder en algunas calculadoras la tecla nPr lo que se formula como P_r^n
Atención: Número asociado al de variaciones sin repetición, le suele corresponder en algunas calculadoras la tecla nPr lo que se formula como P_r^n
- Ejemplo:
nPr(10, 2)da 90.
 En la Vista ComputaciónAlgebraicaSimbólica
En la Vista ComputaciónAlgebraicaSimbólica
En esta vista se admite la misma sintaxis y la inclusión de literales para operar simbólicamente.
- Ejemplos:
nPr(n, 3)es evaluado como n³ - 3 n² + 2 n
n³ - 3 n² + 2 n
{\frac{\Gamma \left( n + 1 \right)}{\Gamma \left( n - 2 \right)} }nPr(n, k)al ser evaluado resulta {\frac{\Gamma \left( n + 1 \right) }{\Gamma \left( -k + n + 1 \right) } }
{\frac{\Gamma \left( n + 1 \right) }{\Gamma \left( -k + n + 1 \right) } }
Siendo \Gamma \left( n + 1 \right) = n! equivale a \frac{n!}{(n - k)! }
- Nota: Ver también el comando nCr(antes NúmeroCombinatorio).
 Aviso: Este comando, habitual en Probabilidades, se encuadra como de Álgebra, campo en que se emplea con frecuencia.
Aviso: Este comando, habitual en Probabilidades, se encuadra como de Álgebra, campo en que se emplea con frecuencia.
Páginas en la categoría «Comandos de Álgebra»
Las siguientes 27 páginas pertenecen a esta categoría, de un total de 27.
C
- Comando ABase
- Comando Cociente
- Comando CompletaCuadrado
- Comando ComúnDenominador
- Comando Desarrolla
- Comando DesdeBase
- Comando División
- Comando Divisores
- Comando EsPrimo
- Comando FactoresPrimos
- Comando Factoriza
- Comando FactorizaI
- Comando ListaDivisores
- Comando Máximo
- Comando MCD
- Comando MCM
- Comando Mínimo
- Comando NúmeroCombinatorio
- Comando PrimerMiembro
- Comando PrimoAnterior
- Comando PrimoSiguiente
- Comando ProductoEscalar
- Comando ProductoVectorial
- Comando Resto
- Comando SegundoMiembro
- Comando Simplifica
- Comando SumaDivisores