Algebra desde la Barra de Entrada IV

Introducción Operativa
Dando Entrada a Objetos de Definición Algebraica
1. Se les da Nombre a Nuevos Objetos, simplemente anteponiendo su nombre = en la Barra de Entrada a su definición algebraica.
2. Un Producto se establece con un asterisco o espacio entre los factores.
3. ¡GeoGebra es sensible a las minúsculas diferencias!... lo que implica que identifica como distintos los nombres de variables en que solo una mayúscula o un tilde distingue una de otra. Por eso es preciso controlar estas cuestiones tanto al otorgar un nombre como al referirlo.
- Los nombres que otorga GeoGebra, espontáneamente a los objetos creados - sea a partir de una herramienta como desde un comando - presentan ciertas distinciones y así, los de los...
- Puntos son letras mayúsculas. Ejemplo: A = (1, 2) o, en coordenadas polares, B = (2; pi)
- Vectores son letras minúsculas Ejemplo: v = (1, 3)
 Aviso: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
Aviso: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
- Puntos son letras mayúsculas.
- Llevan minúsculas también las...
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados Ejemplo: circunferencia c: (x – 2)^2 + (y – 1)^2 = 16
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados
- Deben anotarse y referirse en minúsculas los nombres de las variables como...
- la independiente x de una función o
- x e y en cualquier expresión - ecuación de una sección cónica, de una inecuación, etc. -. Ejemplo: f(x) = 3*x + 2
4. Para incluir un objeto en una anotación en la Barra de Entrada, es preciso crearlo antes y referirlo por el nombre que lo identifica, recordando distinguirlo con todos los detalles correspondientes (mayúsculas, minúsculas, tildes...). Esto vale tanto para las expresiones algebraicas como para los comandos...
- y = m x + b o y = m f(-b) x + f(b) crea una recta en tanto m como b sean ya:
- números que harán las veces de parámetros (recordar que todo número establecido como tal involucra un deslizador cuyo valor puede modificarse en tanto se lo torne visible en la Vista Gráfica activa.
- Recta[A, B] o Recta[A + b Vector[A, B] , B] crea una recta en tanto exista el punto A y el B y/o el número b.
5. Cada expresión ingresada en la Barra de Entrada se debe confirmar' pulsando la tecla Enter (o Intro como aparece en algunos teclados).
6. Tanto las teclas de atajo (F1) como la opción del Menú de Ayuda, permiten abrir la ventana pertinente para averiguar el modo de empleo de un comando en la Barra de Entrada.
7. Si al ingresar un comando en la Barra de Entrada aparece un error, conviene leer detenidamente el correspondiente mensaje para tener mayores recursos para subsanarlo.
8. Los Comandos se pueden anotar o seleccionar desde la lista próxima a la Barra de Entrada.
9. Tras anotar las dos primeras letras de cualquier comando en la Barra de Entrada, emergen alternativas para su Completado Automático tentativo que permite...
- Seleccionar el adecuado pulsando Enter ( Intro en algunos teclados) para ubicar el cursor entre los corchetes.
- Proseguir anotando las siguientes letras hasta que se despliegue el deseado.
Repertorio de Funciones
Más allá de los polinomios que pueden ingresarse directamente en la Barra de Entrada, es posible apelar a cualquier de los diferentes tipos de funciones disponibles en GeoGebra (sean las trigonométricas, las exponenciales, las de valor absoluto, módulo o resto...). Con las funciones se puede operar como con cualquier otro objeto e incluso combinarse con construcciones geométricas o con datos que se registren en las celdas de una Hoja de Cálculo.
Desafío Periódico
Las ondas de sonido pueden ser matemáticamente representadas como una combinación de sinusoides. Cada nota musical está compuesta de varia sinusoides de formulación y(t) = a sin(ω t + φ) . La amplitud a afecta el volumen y la frecuencia angular ω determina el timbre. El parámetro φ se denomina fase porque la indica en la onda de sonido.
Si dos sinusoides se superponen, interfieren entre sí de modo tal que una amplifica o reduce la amplitud de la otra. Es posible representar este modelo de estudio del fenómeno para examinar casos especiales.
Propuesta
Más allá de estas alternativas en las que podría ahondarse, en este caso apenas se plantea, dadas dos sinusoides obtener su suma y pasar a jugar con sus coeficientes para:
- dar respuesta a algunos interrogantes sobre el efecto de cada coeficiente
- lograr como resultante, un diseño ondulado original para el estampado de tela de tapicería.
Como desafío colateral, se propone indagar si podría resultar una función:
- no periódica o
- de un período mayor o menor que el de sendas sinusoides ingresadas.
Interrogantes
- La resultante de sumar ambas sinusoides, ¿será siempre una función periódica?
- El período de la resultante, ¿podrá ser menor o mayor que el de ambas componentes?
Preparando Coeficientes y Primer Sinusoide
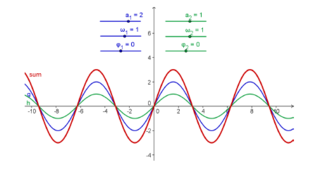
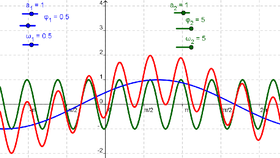
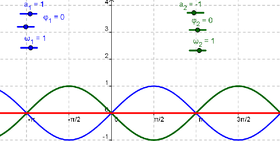
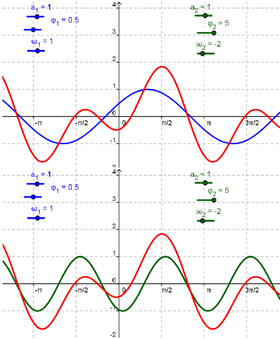
| 1 | Crear tres deslizadores a_1, ω_1, y φ_1 con valores iniciales 1, 1 y 0 respectivamente. | |
| 2 | g(x)= a_1 sin(ω_1 x + φ_1) | Ingresar a continuación la función seno g |
(a) Examinar el impacto de los parámetros - cambio de los valores de los deslizadores - sobre el gráfico de la función sinusoidal. (b) Anticipar el resultado de...
- redefinir g(x) como:
- g(x)= x sin(ω_1 x + φ_1) y como
- g(x)= (1/x) sin(ω_1 x + φ_1)
- corroborar las presunciones con los correspondientes ensayos
- volver a la definición original de g(x) - g(x)= a_1 sin(ω_1 x + φ_1) -
Sumando Sinusoides
| 3 | Crear tres deslizadores a_2, ω_2, y φ_2 | |
| 4 | h(x)= a_2 sin(ω_2 x + φ_2) | Ingresar la otra función seno - h - |
| 5 | sum(x) = g(x) + h(x) | Anotar la suma de ambas funciones en la Barra de Entrada |
(b) Cambiar el color de las tres funciones para distinguirlas con más facilidad.
(c) Fijar a_1 = 1, ω_1 = 1, y φ_1 = 0.
(d) Operar sobre los deslizadores para dar respuesta a los siguientes interrogantes:
- Buscar valores de a_2, ω_2, y φ_2 que afecten a la suma de distintas formas.
- Para que su amplitud sea máxima
 Atención: En este caso, si se tratara de ondas de sonido, el tono resultante tendría volumen máximo.
Atención: En este caso, si se tratara de ondas de sonido, el tono resultante tendría volumen máximo.
- Incluso...
- Para que module la amplitud de g(x) a lo largo de todo su período.
- Para que la onda de salida tenga amplitud nula.
- ¿Para cuáles las dos funciones se cancelan mutuamente?
 Atención: En este caso, si se tratara de ondas de sonido, el tono dejaría de ser audible.
Atención: En este caso, si se tratara de ondas de sonido, el tono dejaría de ser audible.
- Nota:
Para profundizar y ampliar lo que se estudia en este tutorial, es aconsejable consultar: