Circle Command

From GeoGebra Manual
- Circle[Point M, Number r]
- Yields a circle with midpoint M and radius r.
- Circle[Point M, Segment]
- Yields a circle with midpoint M whose radius is equal to the length of the given segment.
- Circle[Point M, Point A]
- Yields a circle with midpoint M through point A.
- Circle[Point A, Point B, Point C]
- Yields a circle through the given points A, B and C.
Note: Also see tools Compass, Circle with Center through Point, Circle with Center and Radius, and Circle through Three Points.
Comments
Tips[edit]
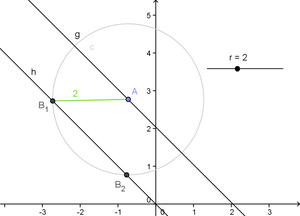
Use circles to fix the distance between two objects[edit]
Circles are a great way to make the distance between two objects constant: If there are two points A and B on two lines g (point A) and h (point B) where A can be moved and B should have the constant distance r to A you can define B as the intersection between the line h and the circle around A with the radius r. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection.