Difference between revisions of "Circle Command"

From GeoGebra Manual
(Created page with 'Circle[Point M, Number r]: Yields a circle with midpoint M and radius r. Circle[Point M, Segment]: Yields a circle with midpoint M whose radius is equal to the length of the gi...') |
({{Note|1=If you use eg <code>x = 0</code> or <code>y = 0</code> for the ''Direction'' it will be interpreted as a plane, not a line }}) |
||
| (31 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Circle | + | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|conic}} |
| + | ;Circle( <Point>, <Radius Number> ):Yields a circle with given center and radius. | ||
| + | ;Circle( <Point>, <Segment> ):Yields a circle with given center and radius equal to the length of the given segment. | ||
| + | ;Circle( <Point>, <Point> ):Yields a circle with given center through a given point. | ||
| + | ;Circle( <Point>, <Point>, <Point> ):Yields a circle through the three given points (if they do not lie on the same line). | ||
| − | + | {{Note|1=See also [[File:Mode compasses.svg|link=|20px]] [[Compass Tool|Compass]], [[File:Mode circle2.svg|link=|20px]] [[Circle with Center through Point Tool|Circle with Center through Point]], [[File:Mode circlepointradius.svg|link=|20px]] [[Circle with Center and Radius Tool|Circle with Center and Radius]], and [[File:Mode circle3.svg|link=|20px]] [[Circle through 3 Points Tool|Circle through 3 Points]] tools.}} | |
| − | + | <br> | |
| − | + | ;Circle( <Line>, <Point> ) | |
| − | + | :Creates a circle with line as axis and through the point. | |
| − | + | ;Circle( <Point>, <Radius>, <Direction> ) | |
| − | + | :Creates a circle with center, radius, and axis parallel to direction, which can be a line, vector or plane. | |
| − | + | :{{example| 1=<div><code><nowiki>Circle( <Point>, <Radius>, <Plane> )</nowiki></code> yields a circle parallel to the plane and with perpendicular vector of the plane as axis.</div>}} | |
| − | + | ;Circle( <Point>, <Point>, <Direction> ) | |
| − | + | :Creates a circle with center, through a point, and axis parallel to direction. | |
| + | {{Note|1=If you use eg <code>x = 0</code> or <code>y = 0</code> for the ''Direction'' it will be interpreted as a plane, not a line }} | ||
Latest revision as of 14:18, 10 July 2018
- Circle( <Point>, <Radius Number> )
- Yields a circle with given center and radius.
- Circle( <Point>, <Segment> )
- Yields a circle with given center and radius equal to the length of the given segment.
- Circle( <Point>, <Point> )
- Yields a circle with given center through a given point.
- Circle( <Point>, <Point>, <Point> )
- Yields a circle through the three given points (if they do not lie on the same line).
Note: See also  Compass,
Compass,  Circle with Center through Point,
Circle with Center through Point,  Circle with Center and Radius, and
Circle with Center and Radius, and  Circle through 3 Points tools.
Circle through 3 Points tools.
- Circle( <Line>, <Point> )
- Creates a circle with line as axis and through the point.
- Circle( <Point>, <Radius>, <Direction> )
- Creates a circle with center, radius, and axis parallel to direction, which can be a line, vector or plane.
- Example:
Circle( <Point>, <Radius>, <Plane> )yields a circle parallel to the plane and with perpendicular vector of the plane as axis.
- Circle( <Point>, <Point>, <Direction> )
- Creates a circle with center, through a point, and axis parallel to direction.
Note: If you use eg
x = 0 or y = 0 for the Direction it will be interpreted as a plane, not a lineComments
Tips[edit]
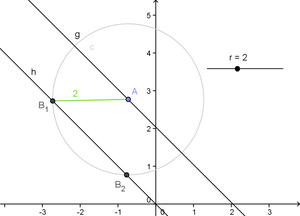
Use circles to fix the distance between two objects[edit]
Circles are a great way to make the distance between two objects constant: If there are two points A and B on two lines g (point A) and h (point B) where A can be moved and B should have the constant distance r to A you can define B as the intersection between the line h and the circle around A with the radius r. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection.