Difference between revisions of "Circle Command"
From GeoGebra Manual
m (Text replace - "<div class="box info"> 48px|left This page is part of the official manual for print and pdf. For structural reasons normal users can't edit this page. If you found any errors on this page please contact ) |
({{Note|1=If you use eg <code>x = 0</code> or <code>y = 0</code> for the ''Direction'' it will be interpreted as a plane, not a line }}) |
||
| (13 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <noinclude>{{Manual Page|version= | + | <noinclude>{{Manual Page|version=5.0}}</noinclude>{{command|conic}} |
| − | {{command|conic}} | + | ;Circle( <Point>, <Radius Number> ):Yields a circle with given center and radius. |
| − | ;Circle | + | ;Circle( <Point>, <Segment> ):Yields a circle with given center and radius equal to the length of the given segment. |
| − | ;Circle | + | ;Circle( <Point>, <Point> ):Yields a circle with given center through a given point. |
| − | ;Circle | + | ;Circle( <Point>, <Point>, <Point> ):Yields a circle through the three given points (if they do not lie on the same line). |
| − | ;Circle | ||
| − | + | {{Note|1=See also [[File:Mode compasses.svg|link=|20px]] [[Compass Tool|Compass]], [[File:Mode circle2.svg|link=|20px]] [[Circle with Center through Point Tool|Circle with Center through Point]], [[File:Mode circlepointradius.svg|link=|20px]] [[Circle with Center and Radius Tool|Circle with Center and Radius]], and [[File:Mode circle3.svg|link=|20px]] [[Circle through 3 Points Tool|Circle through 3 Points]] tools.}} | |
| − | {{ | + | <br> |
| − | }} | + | ;Circle( <Line>, <Point> ) |
| + | :Creates a circle with line as axis and through the point. | ||
| + | ;Circle( <Point>, <Radius>, <Direction> ) | ||
| + | :Creates a circle with center, radius, and axis parallel to direction, which can be a line, vector or plane. | ||
| + | :{{example| 1=<div><code><nowiki>Circle( <Point>, <Radius>, <Plane> )</nowiki></code> yields a circle parallel to the plane and with perpendicular vector of the plane as axis.</div>}} | ||
| + | ;Circle( <Point>, <Point>, <Direction> ) | ||
| + | :Creates a circle with center, through a point, and axis parallel to direction. | ||
| + | {{Note|1=If you use eg <code>x = 0</code> or <code>y = 0</code> for the ''Direction'' it will be interpreted as a plane, not a line }} | ||
Latest revision as of 14:18, 10 July 2018
- Circle( <Point>, <Radius Number> )
- Yields a circle with given center and radius.
- Circle( <Point>, <Segment> )
- Yields a circle with given center and radius equal to the length of the given segment.
- Circle( <Point>, <Point> )
- Yields a circle with given center through a given point.
- Circle( <Point>, <Point>, <Point> )
- Yields a circle through the three given points (if they do not lie on the same line).
Note: See also 
Compass, 
Circle with Center through Point, 
Circle with Center and Radius, and 
Circle through 3 Points tools.
Compass, Circle with Center through Point, Circle with Center and Radius, and Circle through 3 Points tools.
- Circle( <Line>, <Point> )
- Creates a circle with line as axis and through the point.
- Circle( <Point>, <Radius>, <Direction> )
- Creates a circle with center, radius, and axis parallel to direction, which can be a line, vector or plane.
- Example:
Circle( <Point>, <Radius>, <Plane> )yields a circle parallel to the plane and with perpendicular vector of the plane as axis.
- Circle( <Point>, <Point>, <Direction> )
- Creates a circle with center, through a point, and axis parallel to direction.
Note: If you use eg
x = 0 or y = 0 for the Direction it will be interpreted as a plane, not a lineComments
Tips[edit]
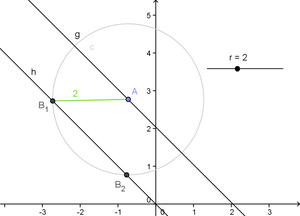
Use circles to fix the distance between two objects[edit]
Circles are a great way to make the distance between two objects constant: If there are two points A and B on two lines g (point A) and h (point B) where A can be moved and B should have the constant distance r to A you can define B as the intersection between the line h and the circle around A with the radius r. As a circle intersects a line at two points (in case it's not tangetial or passing by) you have to hide & ignore the second intersection.
